
2.3. Расчет эксергетического кпд
Основной задачей расчетов является определение эксергетического коэффициента полезного действия ηе:
ηе=
где ΣД- потеря внутренней эксергии в аппарате, находим по формуле:
ΣД = Дс + Дт,
здесь Дт - техническая потеря эксергии, связанная с гидравлическим сопротивлением при теплообмене, находим по формуле:
Дm=Nкн+Nвн,
где NKH, NBH - мощность, затрачиваемая соответственно на перемещение греющего и нагреваемого теплоносителя;
Дс - собственная потеря эксергии, вызванная неравновесным теплообменом определяем по формуле:
Дс=Qв∙∆τе,
где QB- теплопроизводительность;
∆τе — разность эксергетических температур, найденная по формуле:
∆τе = τе1- τе2,
где τе1и τе2- средние термодинамические эксергетические температуры, равные:
 τе1=
τе1= ,
,
τе2=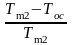 ,
,
где Тm1 , Тm2 - средние термодинамические температуры соответственно греющего и нагреваемого теплоносителей, находим по формулам:
Tm1= ,
,
Tm2= ,
,
где Т’1 , Т" 1- температура греющего теплоносителя на входе и выходе ТОА;
Т'2,Т”2-температура нагреваемого теплоносителя на входе и выходе ТОА;
Тос- температура окружающей среды, принимаем Тос = 293,15 К.
е’1,е"1- удельная эксергия греющего теплоносителя на входе и выходе ТОА соответственно, находим по формуле:
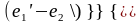 =cp
=cp ∙
∙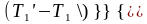 -Tос∙(
cp
-Tос∙(
cp ∙ln
∙ln -
cp
-
cp ∙ln
∙ln ),
),
где cp , cp , cp - соответственно средняя теплоемкость греющего
теплоносителя и средние теплоемкости греющего теплоносителя при средних температурах;
Ма - массовый расход греющего теплоносителя.
Расчет для варианта № 1:
Средние термодинамические температуры греющего и нагреваемого теплоносителей:
Tm1=
= =413,07
К
=413,07
К
Tm2=
= =373,13
К
=373,13
К
Среднетермодинамические эксергетические температуры:
τе1=
= =0,290
=0,290
τе2=
= =0,214
=0,214
Разность эксергетических температур:
∆τе = τе1- τе2=0,290-0,214=0,076
4. Разность удельных эксергий:
 =cp
∙
=cp
∙ -Tос∙(
cp
∙ln
-
cp
∙ln
)=
-Tос∙(
cp
∙ln
-
cp
∙ln
)=
=cp ∙
∙ -293,15∙(cp
-293,15∙(cp ∙ln
∙ln -cp
-cp ∙ln
∙ln )=4,287∙
)=4,287∙
20-293,15∙(4,2015∙0,367-4,191∙0,319)=25,638
5. Эксергетический КПД:
ηе= =
=
 =0,126
или
12,6 %.
=0,126
или
12,6 %.
Расчет для варианта № 2:
Средние термодинамические температуры греющего и нагреваемого теплоносителей:
Tm1=
= =393,07
К
=393,07
К
Tm2=
= =373,13
К
=373,13
К
Среднетермодинамические эксергетические температуры:
τе1=
= =0,254
=0,254
τе2= = =0,214
Разность эксергетических температур:
∆τе = τе1- τе2=0,254-0,214=0,040
Разность удельных эксергий:
=cp ∙ -Tос∙( cp ∙ln - cp ∙ln )=
=cp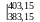 ∙
∙ -293,15∙(cp
∙ln
-cp
-293,15∙(cp
∙ln
-cp ∙ln
∙ln )=4,25∙
)=4,25∙
20-293,15∙(4,191∙0,319-4,183∙0,268)=21,713
5.Эксергетический КПД:
ηе=
=
 =0,081
или
8,1 %.
=0,081
или
8,1 %.
Расчет для варианта № 3:
Средние термодинамические температуры греющего и нагреваемого теплоносителей:
Tm1=
= =383,06
К
=383,06
К
Tm2= = =373,13 К
Среднетермодинамические эксергетические температуры:
τе1=
= =0,235
=0,235
τе2= = =0,214
Разность эксергетических температур:
∆τе = τе1- τе2=0,235-0,214=0,021
4. Разность удельных эксергий:
=cp ∙ -Tос∙( cp ∙ln - cp ∙ln )=
=cp ∙
∙ -293,15∙(cp
-293,15∙(cp ∙ln
∙ln -cp
-cp ∙ln
∙ln )=4,233∙
)=4,233∙
20-293,15∙(4,187∙0,293-4,179∙0,241)=20,269
5. Эксергетический КПД:
ηе=
=
 =0,059
или
5,9 %.
=0,059
или
5,9 %.
Расчет для варианта № 4:
Средние термодинамические температуры греющего и нагреваемого теплоносителей:
Tm1= = =383,06 К
Tm2= = =373,13 К
Среднетермодинамические эксергетические температуры:
τе1= = =0,235
τе2= = =0,214
Разность эксергетических температур:
∆τе = τе1- τе2=0,235-0,214=0,021
4. Разность удельных эксергий:
=cp ∙ -Tос∙( cp ∙ln - cp ∙ln )=
=cp ∙ -293,15∙(cp ∙ln -cp ∙ln )=4,233∙
20-293,15∙(4,187∙0,293-4,179∙0,241)=20,269
5. Эксергетический КПД:
ηе=
=
 =0,058
или
5,8 %.
=0,058
или
5,8 %.
