С этим обозначением систему перепишем в виде

BV +W = 0. (4.10)

Если матрицу В представить так:

(4.11)

то (4.10) в подробной записи будет иметь вид (4.2).

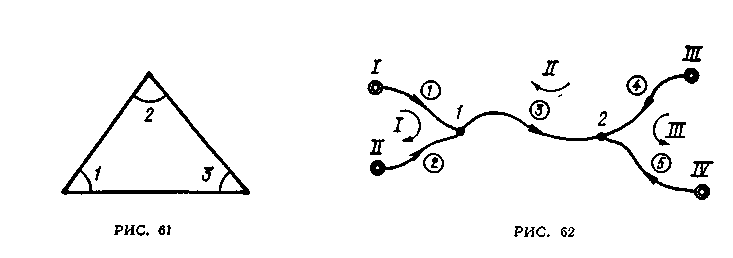
Пример 1. Перейти от параметрического способа к коррелатному при уравнивании трех углов, измеренных в треугольнике (рис. 61). В качестве необходимых неизвестных выберем углы 1 и 2. Тогда уравнения поправок будут

; ;

Приняв в качестве приближенных значений , где — измеренные значения углов, будем иметь свободные члены

, и

где — так называемая невязка. Поэтому

; ;

В этой системе матрицы

; ;

Поэтому согласно формулам (4.9) и (4.7) находим В = (—1 —1 —1),

w = L2 = —W и, наконец, получаем условное уравнение

или

(4.12)

Пример 2. Перейти от параметрического способа уравнивания к коррелатному в нивелирной сети (рис. 62). Здесь уравнения поправок имеют вид:

Перепишем эту систему в виде

(4.13)

Как и в предыдущей задаче, матрица

матрица

.

Поэтому матрица

.

Вектор

.

Так как свободные члены

то

,

.

Поскольку вектор V согласно расстановке уравнений в (4.13)

то получим условные уравнения

Легко видеть, что эти условные уравнения можно написать сразу, выбрав в сети три полигона и придав им направления, как показано на рис. 62.

Ясно, что можно получить и иное решение задачи, если в первую группу отнести иные уравнения поправок, например для v₁ и v₃,, v₁

и v₅ и др. В зависимости от этого будем получать и иные условные уравнения. Число s таких систем условных уравнений совпадает с определителем матрицы [6], т. е. s = det , где — матрица коэффициентов нормальных уравнений, составляемых по способу узлов проф. В. В. Попова при условии, что все ходы имеют одинаковые веса, равные 1. Так, для сети (см. рис. 62)

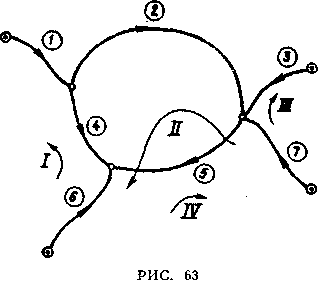
и s = 9 — 1 = 8. Для сети (рис. 63) матрица

.

Определитель этой матрицы найдем по известному правилу (путем присоединения справа двух первых столбцов)

Таблица 97

Номер дерева	Ветви дерева	Номер дерева	Ветви дерева
I	1, 3, 6	13	3, 5, 4
2	1, 7, 6	14	7, 5, 4
3	1, 2, 6	15	3, 2, 4
4	1, 2, 5	16	7, 2, 4
5	1, 4, 5	17	6, 4, 5
6	1, 3, 4	18	1, 2, 4
7	1, 4, 7	19	7, 2, 5
8	6, 4, 2	20	3, 2, 5
9	6, 4, 3	21	2, 7, 6
10	6, 5, 2	22	2, 3, 6
11	6, 4, 7	23	1, 5, 7
12	6, 5, 1	24	1, 3, 5

Совокупность всех измерений, отнесенных в первую группу, на языке теории графов называется деревом сети. Число таких деревьев равно s.

1. Составить деревья в сети (см. рис. 62) и по каждому дереву получить систему условных уравнений.

2. Перейти к системе условных уравнений в нивелирной сети (см. рис. 64) по одному из следующих деревьев (табл. 97).

Например, вариант 11 приведет к выбору полигонов, показанных на рис. 63.

3. Доказать, что матрицы коэффициентов условных уравнений и уравнений поправок связаны соотношением ВА = 0. Проверить это свойство в задаче 4.2.

4. Перейти от уравнений поправок к условному уравнению в задачах 3.36, 3.37. Обращение и перемножение матриц выполнить на ЭВМ «Наири-К» по стандартным программам.

5. Перейти от параметрического способа к коррелатному в сети триангуляции с измеренными углами (см. рис. 52, задача 3.38), отнеся в первую группу уравнения поправок для углов 2, 3, 7, 8, которых достаточно для однозначного определения координат пунктов Д и С.

6. Исходя из параметрического способа, составить условные уравнения при многократном измерении одной и той же величины.

Переход от параметрического способа к коррелатному выполняют в том случае, когда условные уравнения имеют сложный вид.

Переход от коррелатного способа к параметрическому делают значительно реже и выполняют следующим образом. Из общего числа п поправок v_i выбирают к поправок и пишут выражения

; ;…; .

После этого систему условных уравнений записывают в виде

и выражают вектор

.

Тогда получают систему уравнений поправок

; ,

Где матрицы

3. Перейти от условного уравнения (см. пример 1) к уравнениям поправок.

Решение. Пусть

, ,

тогда

откуда

Уравнения поправок

, , ,

где

3. Перейти от условных уравнений в примере 2 к уравнениям поправок.

§39. Коррелатный способ уравнивания. Условные и нормальные уравнения, их решение

Рассмотренные в предыдущем параграфе условные уравнения, как правило, составляют независимо от параметрического способа уравнивания, исходя из геометрических связей, возникающих в сети. В самом деле, каждое избыточное измерение приводит к образованию точной математической зависимости между истинными значениями измеренных величин (условное уравнение связи)

(4.14)

Всего таких уравнений, которые назовем исходными уравнениями связи, будет Например, если Y_i — углы треугольника, то

.

Приводя (4.14) к линейному виду путем разложения в ряд Тейлора и приняв в качестве приближенных значений , где

- измеренные значения, получим

(4.15)

Введя обозначения

, , ,

(4.16)

и учитывая, что разности y_i — Y_i = есть истинные ошибки измерений, вместо (4.15) напишем

(4.17)

Система (4.17), состоящая из r уравнений с n неизвестными, имеет множество решений относительно _i. Поэтому она не может быть решена однозначно. Из всего множества решений выберем такие неизвестные , которые удовлетворяют условию метода наименьших квадратов

(4.18)

или

(4.18')

соответственно для равноточных и неравноточных измерений. Величины v_i назовем поправками. Система

(4.19)

носит название условных уравнений поправок (условных уравнений). Для отыскания относительного минимума функций (4.18) и (4.18') необходимо применить метод Лагранжа, согласно которому составляем функцию

где — неопределенные пока множители Лагранжа. Беря производные от Ф по v_i ,и приравнивая их к нулю, а также обозначая для удобства , получаем после деления на —2 выражения

(4.20)

определяющие поправки через так называемые коррелаты k_j. Для случая неравноточных измерений аналогично получим

(4.21)

Для определения коррелат k_j, подставив выражения (4.20) или (4.21) в (4.19), получим соответственно для случая равноточных и неравноточных измерений систему уравнений

(4.22)

или

(4.23)

где обратные веса.

Выражение (4.22) или (4.23) называют системой нормальных уравнений коррелат.

От аналогичной системы, возникающей в параметрическом способе, она по виду отличается лишь свободными членами, которые теперь не связаны с коэффициентами a_i, b_i, ..., g_i. Величины w_j, вычисленные по формуле (4.16) и представляющие собой приближенные значения функций , вычисленных по измеренным значениям у_i называют невязками условных уравнений.

В матричной форме условные уравнения (4.19) записываются в виде:

(4.24)

а нормальные уравнения

(4.25)

где матрица

(4.25')

Вектор поправок

(4.26)

что соответствует равенствам (4.21).

В теории коррелатного способа уравнивания доказывается, что

(4.27)

(4.28)

или

(4.29)

где величины

(4.30)

а величины

Алгоритмы с одной буквой , раскрываются точно так же, как и алгоритмы и т. д. в параметрическом способе уравнивания, например:

и т. д. Раскрытие алгоритмов выполняется по формулам

и т. д., подобно тому, как раскрываются аналогичные алгоритмы в параметрическом способе. Если условно обозначить

(4.31)

и

(4.32)

то алгоритмы , будут раскрываться так же, как и алгоритмы , в параметрическом способе сравнивания. Тогда вместо (4.27) и (4.28) условно можно написать

С учетом сказанного схема составления нормальных уравнений и их решения методом Гаусса для равноточных измерений дана в табл. 98, 99, 100.

Таблица 98

Номера измерений
1 2 … п		…	…	…

Таблица 99

	a]	b]	…	g]	s’]	контроль
[a [b … [g			… …	…	…		…	…

Равенство является заключительным контролем преобразований в схеме Гаусса.

После вычисления поправок v_i, которые записываются в последний столбец табл. 98, выполняются контроли, подтверждающие правильность вычисления поправок v_i.

; (4.33)

Окончательным контролем решения задачи является выполнение равенств

(4.34)

Таблица 100

Вспомогательные величины					контроль
	-1
	……	………
		-1
	1	1…1

где

— уравненные значения измеренных величин. Иными словами, невязки всех условных уравнений, вычисленных по уравненным результатам измерений, должны быть равны нулю.

Часто применяют такие контрольные формулы:

(4.35)

Следует, однако, заметить, что они контролируют лишь правильность вычисления поправок. Однако если в вычислении коэффициентов условных уравнений допущены ошибки, что особенно вероятно, когда исходные функции (4.14) нелинейные, геодезическая сеть окажется неуравненной даже при соблюдении равенств (4.35). Над столбцами w и 2 в табл. 100 делают такие же преобразования, как и под столбцами l и s в параметрическом способе. Коррелаты k_j вычисляются

Таблица 101

Номера измерений

Таблица 102

	a]	b]	c]	s’]	Контроль

точно так же, как и неизвестные xj, и притом по тем же формулам, если иметь в виду условные обозначения (4.31). Вспомогательные величины k_j вычисляются по столбцу 2 точно так же, как и xj. Говоря проще, если в параметрическом способе в схеме Гаусса в столбцы

Таблица 103

Номера измерений	Коэффициенты условных уравнений						vi
							-2.1 -2.8 -0.5
							2.0 1.7 3.4
							-2.8 -2.1 0.4

Таблица 104

	a]	b]	c]	d]	l]	s']	Контроль		
[a	3	0	0	1	—2,043	1,957	1,957	5,4	7,357
[b		3	0	1	1	5,000	5,000	-7.1	—2,100
[c			3	1	3,057	7,057	7,057	4,5	11,557
[d				3	—0,149	5 851	5,851	3,2	9,051
[l					9,406	11,271	11,271	3,2	14,471

l и s поместить числа из столбцов w и , то вычисления будут выполняться точно так же и по тем же формулам, что и в параметрическом способе.

В случае неравноточных измерений схема сотавления нормальных уравнений состоит из табл. 101 и табл. 102 (здесь для сокращения записей принято r=3).

Решение нормальных уравнений выполняется так же, как и в случае равно точных измерений.

3. Составить и решить нормальные уравнения коррелат, вычислить поправки углов в задаче 4.5.

Решение. Составление и решение нормальных уравнении выполнено в табл. 103—105.

Поправки v_i , вычисленные по формуле (4.20), приведены в последней графе табл. 103. Для удобства их вычисления в последней строке этой таблицы выписаны вычисленные коррелаты.

Как видно, величины поправок v_i совпали с их значениями, полученными в задаче 3.38 параметрическим способом, что говорит о правильности выполненных вычислений. По этой причине в этой задаче опущены окончательные контроли вычислений, присущие коррелатному способу уравнивания.