Лабораторная работа 2 Анализ распределения ресурсов организации

Цель работы: определение оптимального плана работы организации при ограниченных ресурсах и анализ его изменения при смене параметров внутренней и внешней среды.

Последовательность выполнения работы

1. В табличном редакторе Excel оформить таблицу с исходными данными. Построить систему ограничений и целевую функцию. Определить оптимальный объем выпуска деталей при исходных ограничениях и данных. Провести анализ полноты полученных результатов.

2. Рассчитать три – четыре варианта изменения ресурсов и провести анализ полученных планов работы.

3. Провести анализ изменения плана работы организации при изменении организационной структуры (увеличение числа подразделений) и увеличении числа типов выпускаемых деталей.

4. Рассчитать изменения целевой функции запасов ресурсов на одну единицу, а также верхние и нижние границы устойчивости по ограничениям ресурсов и коэффициентам целевой функции. Определить время окупаемости нового оборудования ценой 1000 рублей, если на одном из участков оно уменьшает загрузку в два раза.

Примечание. При оформлении расчетов предусмотреть возможность изменения значений параметров в исходной таблице и получения результата без изменения расчетной схемы вычислений.

Методические рекомендации

1. Для отладки расчётной схемы и полноты получаемых результатов целесообразно использовать данные простой задачи оптимального распределения ресурсов (например, задача 1.3 из [1].

Исходные данные: На трех участках фирмы обрабатываются два вида деталей. Известна загрузка каждого участка (в процентах) при обработке одной детали и прибыль от реализации одной детали (смотри таблицу 2.1). Необходимо обосновать оптимальный план обработки деталей при полной загрузке участков.

Таблица 2.1 – Исходные данные

Детали	Загрузка участков, %			Прибыль от продажи одной детали, рубль
	№1	№2	№3
Д1	5	1,6	2,9	240
Д2	4	6,4	5,8	320
Макс. загрузка участков	100	100	100

Выполнение работы начинается с оформления шапки отчёта, где в среде Excel указывается сокращённое наименование учебной дисциплины, номер лабораторной работы, фамилия и инициалы студента, дата выполнения работы и номер варианта исходных данных (смотри рисунок 2.1).

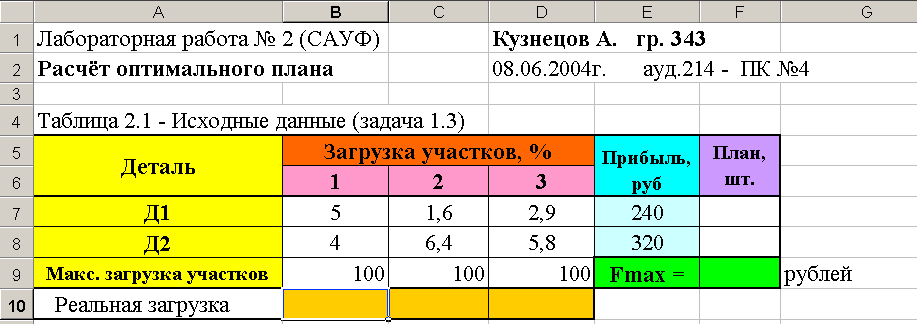
Рисунок 2.1- Пример шапки отчёта, исходных данных и результатов

Для решения задачи надо воспользоваться инструментами Excel:

Сервис Настройка Поиск решения

и подготовить исходные данные для решения задачи (смотри рисунок 2.2).

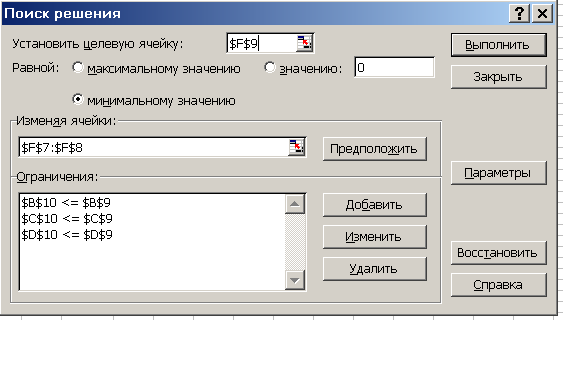
Рисунок 2.2 – Поиск решения

Выполнение расчётов даёт решение задачи (смотри рисунок 2.3).

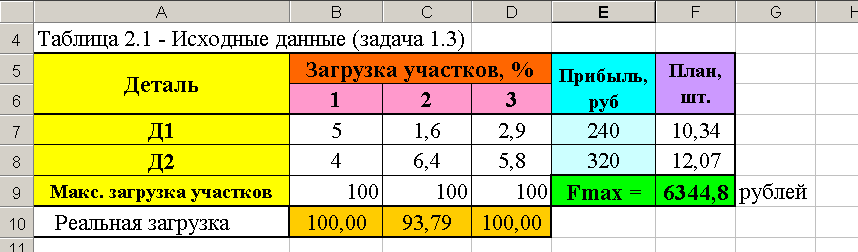
Рисунок 2.3 – Решение задачи 1.3 [1]

Вывод: оптимальный план работы организации соответствует выпуску деталей в количестве 10 и 12 единиц, при этом прибыль составит 6344,8 рублей и будет недогруз участка №2 на 6 процентов.

2. Для расчёта вариантов распределения ресурсов при изменении исходных данных необходимо повторить таблицу 2.1 с изменением показателей (таблица 2.2), рассчитать новый план работы (смотри рисунок 2.4) и сравнить с начальным вариантом.

Основные изменения ресурсов для индивидуальных заданий приведены в таблице 2.2.

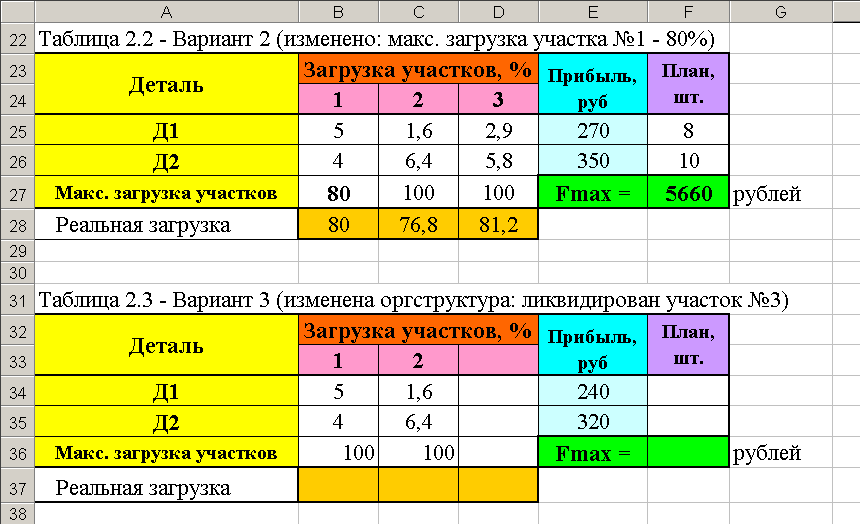
Рисунок 2.4 – Расчёт оптимального плана по вариантам 2 и 3

Таблица 2.2 – Исходные данные для индивидуальных заданий

Номер задания	Изменённая прибыль по деталям		Изменённая макс. загрузка участков			Изменённая загрузка участков по детали Д1 (Д2)			Изменения оргструктуры и типов деталей
	Д1	Д2	№1	№2	№3	№1	№2	№3
1	280	0	80	80	80	6	3,3	(7)	Введён участок №4
2	300	300	70	-	-	-	6	-
3	320	280	60	-	50	-	-	2	Добавлена деталь Д3
4	340	260	50	-	-	(5)	-	-
5	360	240	0	0	0	-	(6)	-
6	230	640	20	-	40	-	(3,3)	2	Введёны участки №4 и №5
7	220	620	-	-	80	8	-	(6)
8	210	600	70	50	-	2,5	-	-
9	0	250	55	-	-	-	10	3	Введён участок №4
10	-	-	48	-	60	3	7	-
11	720	960	-	90	-	2,5	(6)	2	Добавлены детали Д3 и Д4
12	500	1000	47	-	47	-	(3,3)	(6)
13	480	640	0	-	90	6	-	-
14	300	240	45	70	-	-	-	2
15	200	160	80	-	-	-	3,3	(6)
16	120	160	75	-	-	(5)	6	-
17	340	260	50	-	-	-	-	(7)	Добавлена деталь Д3
18	360	240	0	0	0	-	-	-
19	230	640	20	-	40	2,5	9	2	Введён участок №4
20	220	620	-	-	80	-	6	-
21	210	600	70	50	-	2	-	-
22	0	250	55	-	-	6	(6)	-	Добавлены детали Д3 и Д4
23	-	-	48	-	60	-	(3,3)	2
24	720	960	-	90	-	-	-	(7)	Введёны участки №4 и №5
25	500	1000	47	-	47	2,5	-	-
26	480	640	0	-	90	-	3,3	(2)
27	300	240	45	70	-	(5)	6	-
28	200	160	80	-	-	-	-	-	Введён участок №4
29	120	160	75	-	-	-	-	4
30	-	-	-	-	-		3,2	2 (7)	-

3. При изменении организационной структуры организации необходимо повторить пункты 1 и 2 для новых исходных данных (например, вариант 3 на рисунке 2.4).

4. Для расчёта изменения целевой функции при изменении запасов ресурсов на одну единицу, а также верхних и нижних границ устойчивости по ограничениям ресурсов и коэффициентам целевой функции необходимо решить двойственную задачу.

Двойственная задача линейного программирования (ЛП) по отношению к основной задаче ЛП удовлетворяет требованиям [3]:

m

 b_i y_i  min, y_i  0, i=1, 2, …, m,

i=1

m

 a_ij y_i  c_j , j=1, 2, …, n.

i=1

Каждой переменной исходной задачи соответствует переменная двойственной задачи (и наоборот). Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.