4. Парабола

Параболой называется множество всех точек плоскости, каждая из ко­торых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через р (р > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директри­сой (см. рис. 12). В выбранной системе фокус F име­ет координаты , а уравнение директрисы имеет вид х = - , или х + = 0.

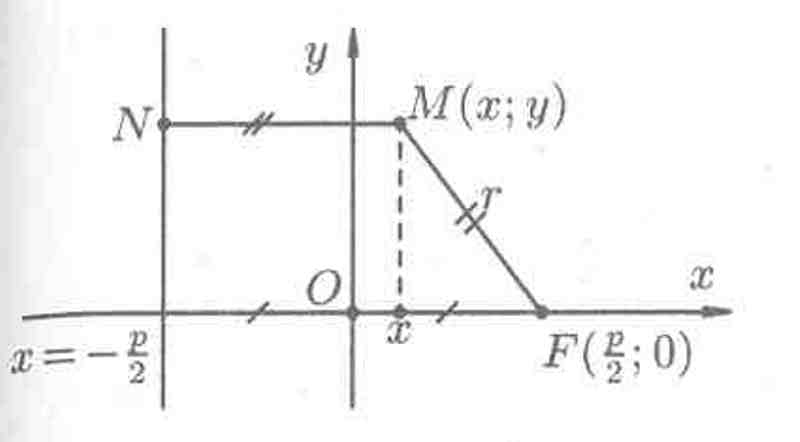
Рис. 12.

Пусть М(х;у) — произвольная точка параболы. Соединим точку М с F. Проведем отрезок MN пер­пендикулярно директрисе. Согласно определению параболы MF = MN. По формуле расстояния между двумя точками на­ходим:

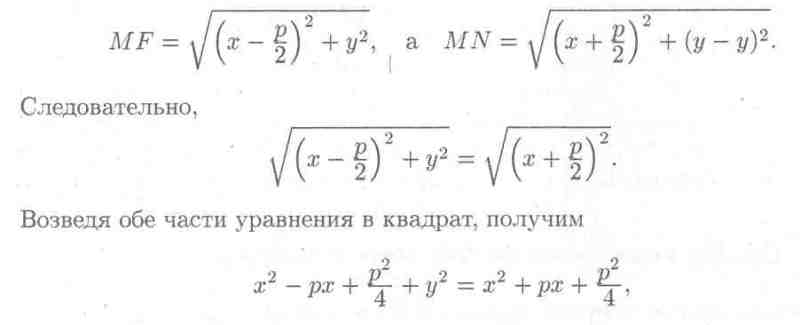
т. е. у² = 2рх.

Уравнение у² = 2рх называется каноническим уравнением параболы.

Пара­бола есть линия второго порядка.

Исследование форм параболы по ее уравнению

1. В уравнении у² = 2рх переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью сим­метрии параболы.

2. Так как р > 0, то из у² = 2рх следует, что х ≥ 0. Следовательно, парабола рас­положена справа от оси Оу.

3. При х = 0 имеем у = 0. Следователь­но, парабола проходит через начало коор­динат.

4. При неограниченном возрастании х модуль у также неограниченно возраста­ет. Парабола у² = 2рх имеет вид (фор­му), изображенный на рисунке 13. Точ­ка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М

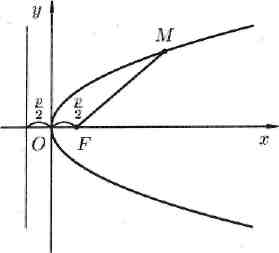
Рис. 13.

Уравнения у² = -2рх, х² = 2ру, х² = -2ру (р > 0) также определяют параболы, они изображены на рисунке 14.

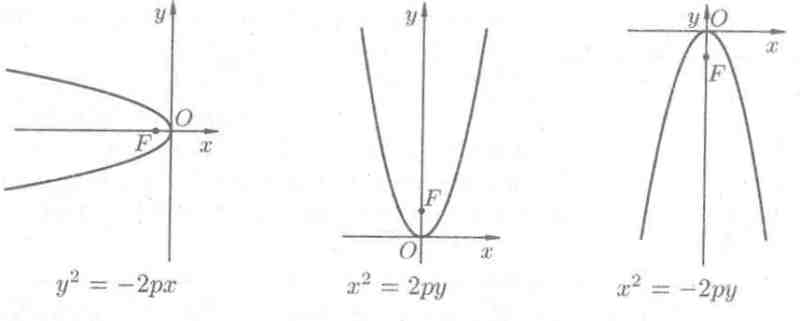
Рис. 14.

Нетрудно показать, что график квадратного трехчлена у = Ах² + + Вх + С, где А -≠ 0, В и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.

5. Общее уравнение линий второго порядка

5.1. Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям

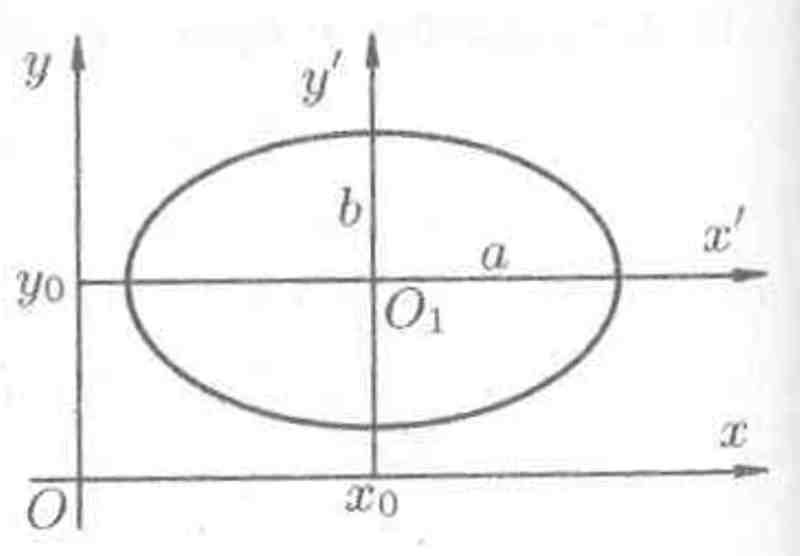
Найдем сначала уравнение эллипса с центром в точке O₁(x₀;y₀), оси симметрии которого параллельны координатным осям Ох и Оу и полуоси соответственно равны а и b. Поместим в центре эллипса O₁ начало новой системы координат O₁x'y', оси которой O₁х' и O₁у' параллельны соответ­ствующим осям Ох и Оу и одинаково с ними направлены (см. рис. 63).

.

Рис. 15.

В этой системе координат уравнение эл­липса имеет вид .

Так как х' = х - x₀, у' = x – у₀ (формулы па­раллельного переноса), то в старой системе координат уравнение эллипса запи­шется в виде .

Аналогично рассуждая, получим уравне­ние гиперболы с центром в точке O₁(х₀;y₀) и полуосями а и b (см. рис. 16):

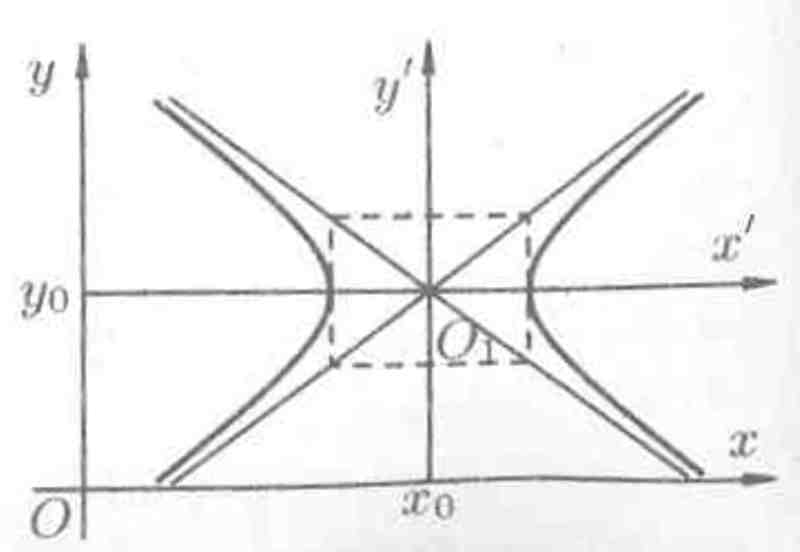
Рис. 16.

И, наконец, параболы, изображенные на рисунке 17, имеют соответству­ющие уравнения:

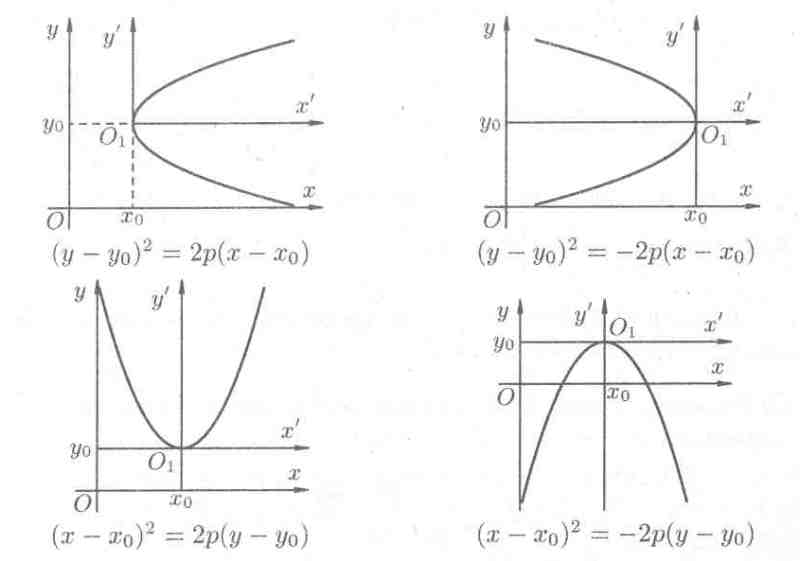
Рис. 17.

5.2. Уравнение Ах² + Су² + 2Dx + 2Еу + F = 0

Уравнения эллипса, гиперболы, параболы и уравнение окружности (х – х₀)² + (у – у₀)² = R² после преобразований (раскрыть скобки, пе­ренести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помо­щью единого уравнения вида:

Ах² + Су² + 2Dx + 2Ey + F = 0, где коэффициенты А и С не равны нулю одновременно.

Возникает вопрос: всякое ли уравнение вида Ах² + Су² + 2Dx + 2Ey + F = 0 определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема:

Теорема 2. Уравнение Ах² + Су² + 2Dx + 2Еу + F = 0 всегда определяет: либо окружность (при А =С), либо эллипс (при А · С > 0), либо гиперболу (при А · С < 0), либо параболу (при А·С = 0).

При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.

Пример 1.

Установить вид кривой второго порядка, заданной урав­нением 4x² + 5у² + 20х - 30у + 10 = 0.

Решение: Предложенное уравнение определяет эллипс (А-С = 4·5 > 0). Действительно, проделаем следующие преобразования:

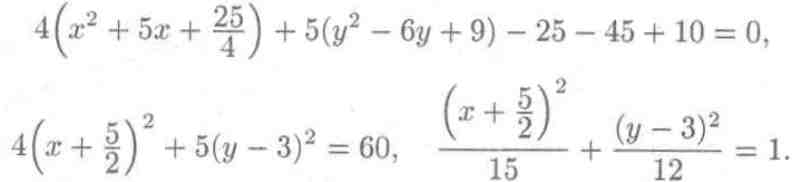
Получилось каноническое уравнение эллипса с центром в O₁( - ;3) и полуосями

а = , b =

Пример 2.

Установить вид кривой второго порядка, заданной урав­нением х² + 10x - 2у + 11 = 0.

Решение: Указанное уравнение определяет параболу (С = 0). Действи­тельно,

x² + 10x + 25 - 2у + 11 - 25 = 0,

(х + 5)² = 2у + 14, (x + 5)² = 2(у + 7).

Получилось каноническое уравнение параболы с вершиной в точке O₁(-5;-7)и р=1.

Пример 3. Установить вид кривой второго порядка, заданной урав­нением 4х² - у² + 8х - 8у - 12 = 0 (А · С = -4 < 0).

Решение: Преобразуем уравнение:

4(х² + 2х + 1) - (у² + 8у + 16) - 4 + 16 - 12 = 0,

4(х + 1)²-(у + 4)² = 0,

(2(х + 1) + (у + 4)) • (2(х +1)-(у + 4)) = 0,

(2х + у + 6) (x - у - 2) = 0.

Это уравнение определяет две пересекающиеся прямые 2х + у + 6 = 0 и 2х - у - 2 = 0.