4. Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов , и основано на следующих соображениях. Если > 0, то , , — правая тройка; если < 0, то , , - левая тройка.
Установление компланарности векторов
Векторы , , компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( ≠ 0, ≠ 0, ≠ 0):
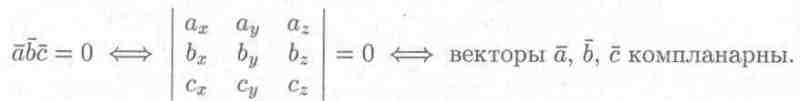
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах , и вычисляется как V = | |, а объем треугольной пирамиды, построенной на этих же векторах, равен V = 1/6| |.
Пример 1. Вершинами пирамиды служат точки А(1; 2; 3), В(0; -1; 1), С(2;5;2) и D(3;0; -2). Найти объем пирамиды.
Решение: Находим векторы , , :
=
=(-l;-3;-2),
=
=
(1;3;-1),
=-
= (2; -2; -5).
Находим
Следовательно,
