2. Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак, т. е. х = - ( х ) (см. рис. 19).

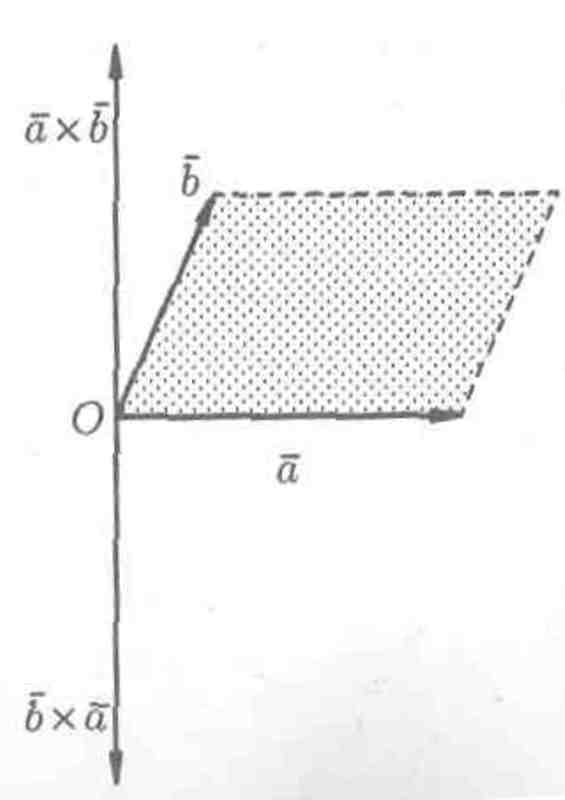
Рис. 19.

Векторы х и х коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки , , х и , , х противоположной ориентации).

Значит, х = - ( х ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. λ( х ) = (λ ) х = х (λ ).

Пусть λ > 0. Вектор λ ( х ) перпендикулярен векторам и . Вектор (λ ) х также перпендикулярен векторам и (векторы , λ лежат в одной плоскости). Значит, векторы λ( х ) и (λ ) х коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

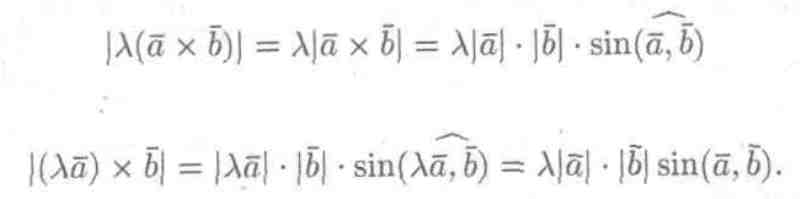
Поэтому λ( х ) и λ х .

3. Два ненулевых вектора а и В коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. || ↔ х = 0.

Если || , то угол между ними равен 0° или 180°. Но тогда | х | = | | • | | • = 0. Значит, х = 0.

Если же х = 0, то | | • | | sin φ = 0. Но тогда φ = 0° или φ = 180°, т. е. || .

В частности, .

4. Векторное произведение обладает распределительным свойством:

( + ) х = х + х .

3. Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения единичных векторов :

			-
	-
		-

Чтобы не ошибиться со знаком, удобно пользоваться схемой:

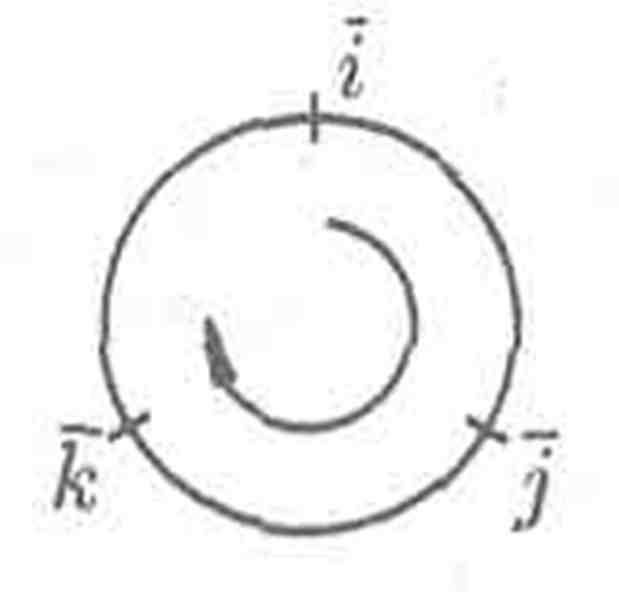
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».

Пусть заданы два вектора = a_x +a_y +a_z и = b_x +b_y +b_z . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

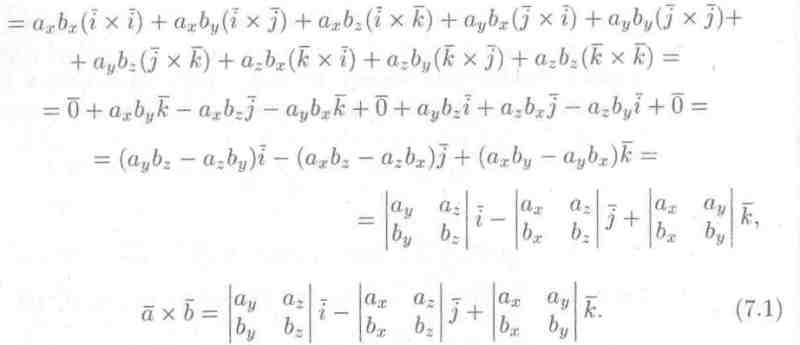
Полученную формулу можно записать еще короче:

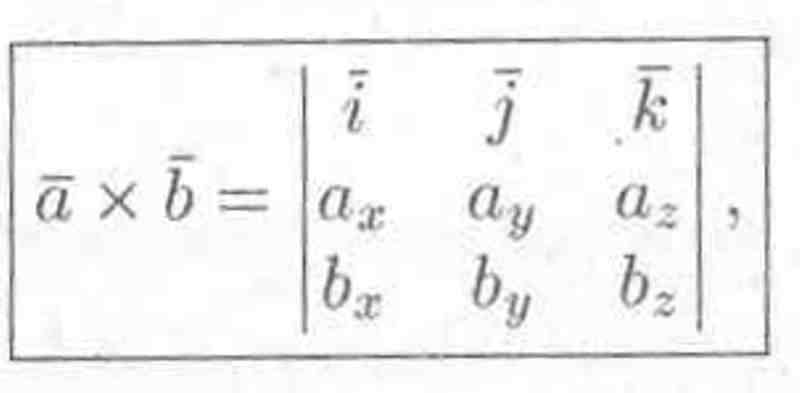
так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки. Данное равенство легко запоминается.

4. Некоторые приложения векторного произведения

Установление коллинеарности векторов

Если || , то х = 0 (и наоборот), т. е.

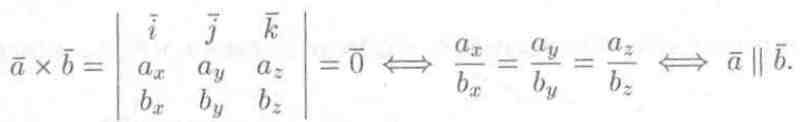
Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов и | x | = = | | · | | sin φ, т. е. S_пар = | х |. И, значит, S_Δ = 1/2| x |.

Определение момента силы относительно точки

Пусть в точке А приложена сила = и пусть О — некоторая точка пространства (рис. 20).

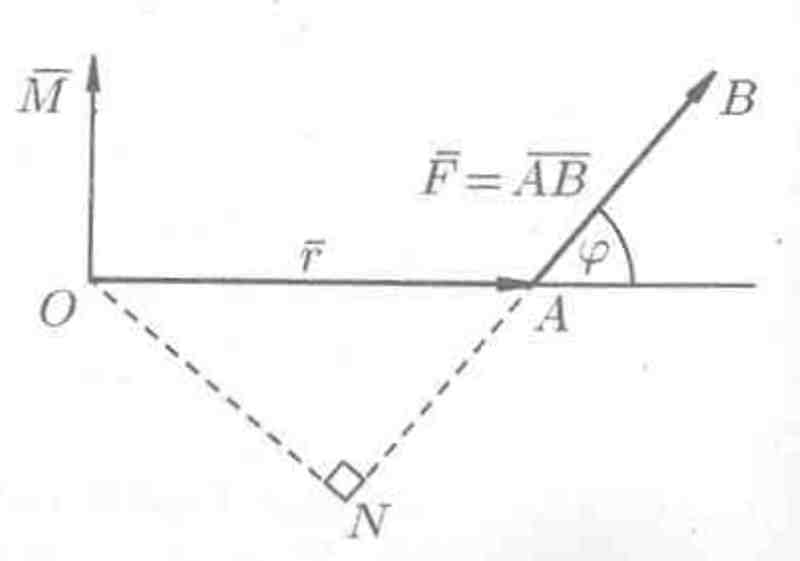
Рис. 20.

Из физики известно, что моментом силы относительно точки О называется вектор , который проходит через точку О и:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2) численно равен произведению силы на плечо

| | = | |·ON = | | • | | sin φ = | |·| | ,

3) образует правую тройку с векторами и .

Стало быть, = х

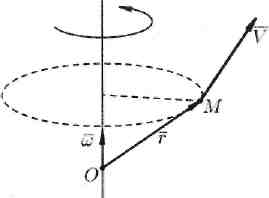Рис. 21.

.

Нахождение линейной скорости вращения

Скорость точки М твердого тела, вращающегося с угловой скоростью во­круг неподвижной оси, определяется формулой Эйлера = х , где = , где О — некоторая неподвижная точка оси (см. рис. 21).