5. Действия над векторами, заданными проекциями

Пусть векторы = (а_х; а_у; a_z) и = (b_х; b_у; b_z) заданы своими проекциями на оси координат Ох, Оу, Oz или, что то же самое

,

Линейные операции над векторами

Так как линейные операции над векторами сводятся к соответствую­щим линейным операциям над проекциями этих векторов, то можно запи­сать:

1. ,

или кратко .

To есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

2. или короче λ = (λа_х; λа_у; λa_z). To есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

Равенство векторов

Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора u равны тогда и только тогда, когда выполняются равенства: а_х = b_х, а_у = b_у, а_z = b_z, т. е.

Коллинеарность векторов

Выясним условия коллинеарности векторов u , заданных своими координатами.

Так как || , то можно записать =λ· , где λ — некоторое число. То есть

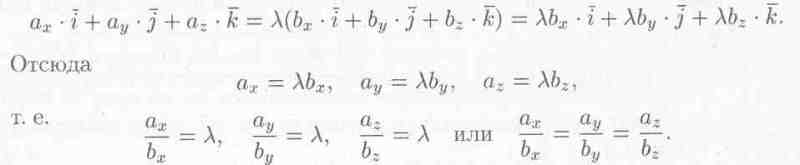
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.

Координаты точки

Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М координаты вектора называются координатами точки М. Вектор называется радиус-вектором точки М, обозначается , т. е. = . Следовательно, координаты точки — это координаты ее радиус-вектора

= (х; у; z) или = x + y + z .

Координаты точки М записываются в виде M (x;y;z).

Координаты вектора

Найдем координаты вектора = , если известны координаты точек A(x₁;y₁;z₁) и В(х₂;у₂;z₂). Имеем (см. рис. 13):

Рис. 13.

Следовательно,

координаты вектора равны разностям соответствующих координат его конца и начала: = (х₂ – х₁; у₂ – y₁; z₂ – z₁).

Лекция 2 « скалярное произведение векторов»

1. Определение скалярного произведения

Скалярным произведением двух ненулевых векторов u называется число, равное произведению длин этих векторов на косинус угла между ними.

О бозначается или · : · = | | · | |·cos φ, где .

Рис. 14.

2. Свойства скалярного произведения

1. Скалярное произведение обладает переместительным свойством: = . =| | · | | • , a = | |·| |· . И так как | | · | | = =| |·| |, как произведение чисел и = , то = .

2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: (λ ) • = λ( ).

(λ ) • =| | пр λ = λ • | | • пр = λ( ).

3. Скалярное произведение обладает распределительным свойством:

( + ) = + .

4. Скалярный квадрат вектора равен квадрату его длины: ² = | |².

² = • = | | • | | cos 0 = | | · | | = | |²

В частности:

Если вектор возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль | |, т. е. = | | ( ≠ ).

Пример.

Найти длину вектора = 3 - 4 , если | | = 2, | | = 3, .

5. Если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если , то = 0. Справедливо и обратное утверждение: если = 0 и ≠ ≠ , то .

Так как , то cos φ = cos π/2 = 0. Следовательно, · =| |· | |·0 = 0. Если же · = 0 и | | ≠ 0, | | ≠ 0, то = 0. Отсюда = 90°, т. е. . В частности: