50

II. Механика

Лабораторная работа №4

Определение скорости распространения

звуковой волны в воздухе

Цель работы: познакомиться с методом определения звука с помощью стоячей волны.

Литература

1.  1 , §§ 7.8, 8.4.

2.  2 , §§ 24, 25.

Вопросы входного контроля

1. Какие вопросы изучаются в разделе физики – «Акустика»?

2. Дать определение механической волны. Каковы ее основные характеристики?

3. Вывести уравнение бегущей волны.

4. Как распространяются механические волны в неоднородных средах?

5. Дать определение стоячей волны. Вывести уравнение стоячей волны и дать его анализ.

6. Как определить скорость звука методом стоячей волны?

1. Краткая теория

В системах, в результате сложения 2-х бегущих, распространяющихся навстречу друг другу, волн одинаковой частоты и сдвига по фазе, возникает качественно новая волна – стоячая. В частности, в среде с ограниченным объемом это результат интерференции (сложения) волн падающей и отраженной.

1. Уравнение стоячей волны

Пусть в однородной полубесконечной среде в точке х=0 находится источник волны (И). Расстояние от источника до границы - . На границе раздела 2-х сред волна частично переходит в другую среду – преломляется, частично возвращается от границы (F) в первую - отражается (см. рис. 1).

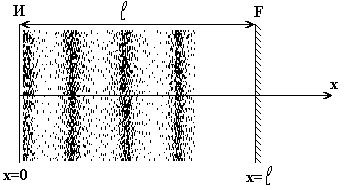
Рис.1.

В каждой точке х волнового поля между точками х = 0 и х = будут складываться колебания, принадлежащие 2-м идущим в разных направлениях волнам – бегущей и отраженной.

Смещение точки от положения равновесия в момент времени t в бегущей волне определяется уравнением:

, (1)

где с – скорость распространения волны в 1-ой среде,

А- амплитуда колебаний,

х – координаты точки.

Чтобы получить смещение от положения равновесия в момент  в отраженной волне (уравнение отраженной волны), необходимо определить время запаздывания  возмущения от генератора до рассматриваемой точки.

Поскольку отраженная волна прошла до границы расстояние l и от границы до точки с координатой х расстояние ( –х) для  имеем:

.

Тогда S2 – смещение от положения равновесия в отраженной волне описывается законом:

(2)

В уравнение (2) учитывается скачкообразное изменение фазы волны на  при отражении. Результирующее смещение получаем, складывая уравнение (1) и (2):

.

Воспользовавшись тригонометрическим сложением косинусов

и формулами приведения имеем:

. (3)

Уравнение (3) является уравнением стоячей волны. Анализ уравнения (3):

При сравнении (3) с уравнением гармонических колебаний:

, (4)

где А – амплитуда, постоянная величина,

- фаза колебаний,

- начальная фаза,

видно:

1. Выражение является амплитудой колебаний в точке с координатой х. После его анализа можно сделать вывод, что амплитуды точек в стоячей волне зависят от координат (в бегущей волне все амплитуды одинаковы). Кроме того, в такой волне есть точки, амплитуда которых максимальна (получаем из условия =1). Эти точки называются пучностями стоячей волны. Точки, в которых амплитуда минимальна (из условия = 0) называются узлами стоячей волны.

2. Фаза колебаний определяется выражением:

.

Как видно, фаза колебаний не зависит от координаты х (в бегущей волне - функция и координаты, и времени).

Но поскольку выражение меняет свой знак при переходе через нуль (узел стоячей волны), все точки между 2-мя соседними узлами имеют смещение одного знака, а между следующими - другого.

3. Выражение играет роль начальной фазы.

В отличие от бегущей волны в стоячей волне нет переноса энергии (с этим связано название волны), т.к. обе волны несут навстречу друг другу в среднем одинаковые энергии.

На рис.2 изображено несколько последовательных положений результирующего смещения в стоячей волне в зависимости от координаты, соответствующих разным моментам времени t₁,t₂,t₃.

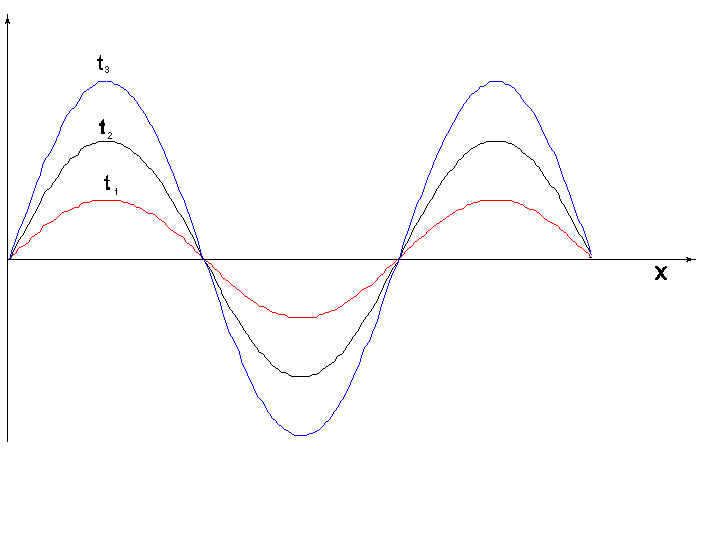
S

Рис. 2.

2. Применение стоячей волны для оценки скорости распространения волн в данной среде

Анализ выражения для амплитуды

позволяет найти положение точек, колеблющихся с максимальной амплитудой 2А, при условии, если:

.

Решая данное тригонометрическое выражение, получаем:

= ,

где n = 0,1,2,…

или, учитывая связь - частоты и с – скорости распространения с  (длиной волны):

= ,

Данное выражение можно преобразовать:

(5)

где - размеры колебательного пространства.

Полученное выражение показывает, что максимальная амплитуда определяется как размерами колебательного пространства ( ), так и положением точки (координата х).

Чтобы данная волна явилась источником колебаний в окружающем пространстве, передающим максимальную энергию (т.е. наблюдался резонанс) необходимо достижение максимальной амплитуды в точке, где х=0.

В этом случае уравнение (5) преобразуется:

. (6)

Из (6) видно, что величина полости, дающая максимальную энергию зависит от длины волны ( ), причем принимает различные значения, определяемые n.

Так для

,

,

.

Условию резонанса (6) подчиняются и звуковые волны. Резонанс проявляется в максимуме звучания. Стоячую волну можно получить при сложении волны от источника (генератора) с волной, отраженной от границы со средой, обладающей значительно большим акустическим импедансом. Такой средой может быть вода. Если звуковая волна с неизменной длинной распространяется в пространстве (полости) с подвижной границей, то при выполнении условия (6) периодически будет возникать максимум звучания.

Итак, резонанс наблюдается, если размеры полости удовлетворяют (6). В практических исследованиях наиболее точно можно измерить разницу в размерах между 2-мя соседними резонирующими областями , которая определяется из отношения:

. (7)

Используя (7), получаем:

. (8)

Поскольку между длиной волны (), скоростью звука (с) и частотой (v) существует связь

, (9)

то можно получить выражение для определения скорости звуковой волны, используя (8) и (9):

. (10)