2 Множественный регрессионный анализ

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, который в свою очередь включает 2 круга вопросов: отбор факторов и выбор уравнения регрессии.

Отбор факторов обычно осуществляется в два этапа:

1) теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;

2) количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции):

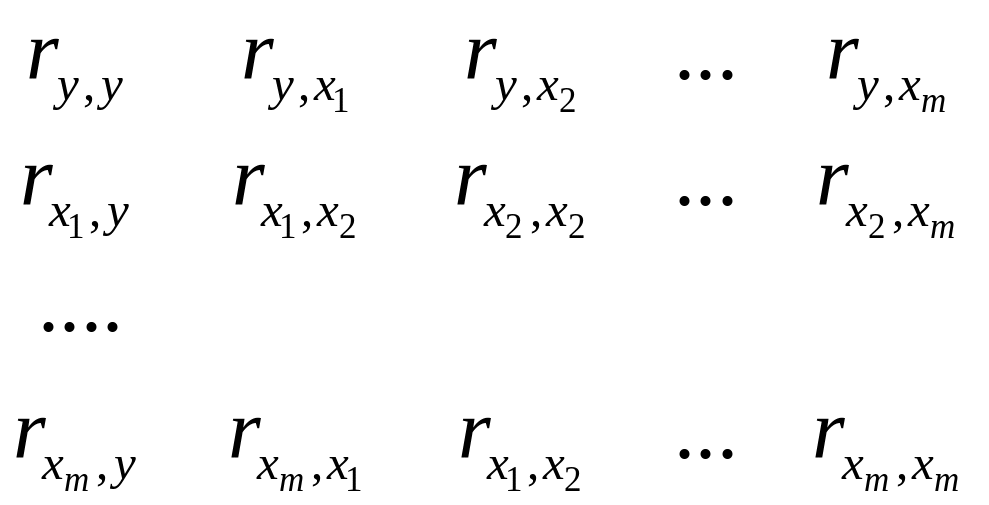
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).

2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной кор­реляции между фактором и результатом должен быть существенным).

3. Факторы не должны быть коррелированны друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированны). Разновидностью интеркоррелированности факторов является мультиколлинеарность - наличие высокой линейной связи между всеми или несколькими факторами.

Мультиколлинеарность может привести к нежелательным последствиям:

1) оценки параметров становятся ненадежными, обнаруживают большие стандартные ошибки и меняются с из­менением объема наблюдений (не только в величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

2) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

3) нельзя определить изолированное влияние факторов на результативный показатель.

Мультиколлинеарность имеет место, если определи­тель матрицы межфакторной корреляции близок к нулю:

Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.

Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них - исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, снизится несущественно).

Определение факторов, ответственных за мультиколлинеарность, может быть основано на анализе матрицы межфакторной корреляции. При этом определяют пару признаков-факторов, которые сильнее всего связаны между собой (коэффициент линейной парной корреляции максимален по модулю). Из этой пары в наибольшей степени ответственным за Мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (имеет более высокие по модулю значения коэффициентов парной линейной корреляции).

Еще один способ определения факторов, ответственных за мультиколлинеарность основан на вычислении ко­эффициентов множественной детерминации , показывающего зависимость каждого фактора от других факторов модели. При этом в качестве зависимой переменной рассматривается каждый из факторов . А в качестве независимых переменных прочие факторы модели . Чем ближе значение коэффициента множественной детерминации к единице, тем больше ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для различных факторов можно проранжировать переменные по степени ответственности за мультиколлинеарность.

При выборе формы уравнения множественной регрес­сии предпочтение отдается линейной функции:

в виду четкой интерпретации параметров.

Данное уравнение регрессии называют уравнением регрессии в естественном (натуральном) масштабе. Коэффициент регрессии при факторе называют условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих средних уровнях).

Если не делать предположения о значениях прочих факторов, входящих в модель, то это означало бы, что каждый из них при изменении также изменялся бы, так как факторы (пусть и несильно) связаны между собой, и своим изменением оказывал бы влияние на признак-результат.

Расчет параметров уравнения линейной множественной регрессии.

Параметры уравнения линейной множественной регрессии можно определить методом наименьших квадратов, как и в случае парной регрессии.

Параметры линейного множественного уравнения регрессии можно определить и другим способом - через β-коэффициенты (параметры уравнения регрессии в стандартных масштабах).

Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:

где - значение переменной

.

Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее . Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:

.

β-коэффициенты могут быть оценены с помощью обычного МНК. При этом система нормальных уравнений будет иметь вид:

Найденные из данной системы β-коэффициенты по­зволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:

.

Показатели тесноты связи факторов с результатом.

Если факторные признаки различны по своей сущно­сти и/или имеют различные единицы измерения, то коэф­фициенты регрессии при разных факторах являются не­сопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с ре­зультатом, позволяющими ранжировать факторы. К ним от­носят: частные коэффициенты эластичности, β-коэффициенты, частные коэффициенты корреляции.

Частные коэффициенты эластичности рассчитываются по формуле: . Частный коэффициент эластичности показывают на сколько процентов в среднем изменяется признак-результат Y с изменением признака-фактора на один процент от своего среднего уров­ня при фиксированном положении других факторов модели. В случае линейной зависимости коэффициент эластичности рассчитывается по формуле: , где - коэффициент регрессии .

Стандартизированные частные коэффициенты регрессии - β-коэффициенты показывают, на какую часть своего среднего квадратического отклонения изменится признак-результат Y с изменением соответствующего фак­тора на величину своего среднего квадратического от­клонения при неизменном влиянии прочих факторов входящих в уравнение.

По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разно­направленное воздействие факторов на результат.

Кроме того, коэффициент может интерпретировать­ся как показатель прямого (непосредственного) влияния фактора на результат . Во множественной регрес­сии фактор оказывает не только прямое, но и косвен­ное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели). Косвенное влияние измеря­ется величиной: , где т- число факторов в модели. Полное влияние фактора на результат равное сумме прямого и косвенного влияний измеряет коэффици­ент линейной парной корреляции данного фактора и ре­зультата – .

Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

Для расчета частных коэффициентов корреляции мо­гут быть использованы парные коэффициенты корреляции.

Для случая зависимости Y от двух факторов можно вычислить 2 коэффициента частной корреляции:

(2-ой фактор фиксирован).

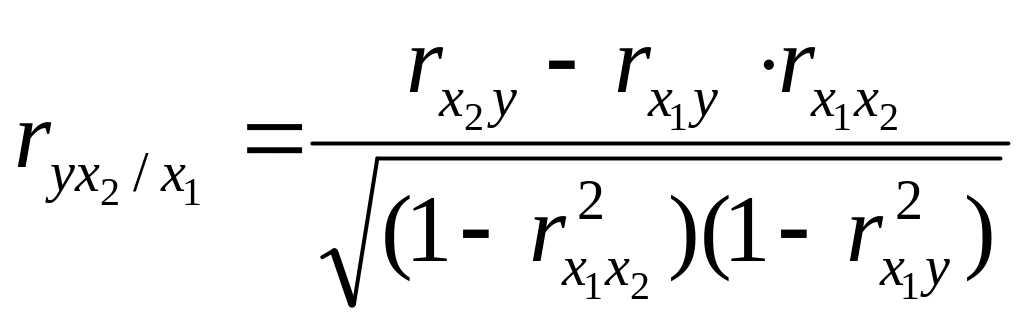(1-ый фактор фиксирован).

Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется).

Частные коэффициенты корреляции, рассчитанные по таким формулам, изменяются от -1 до +1. Они используют­ся не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях нет смысла вводить в уравнение m-ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретиче­ский коэффициент детерминации увеличится незначительно).

Коэффициенты множественной детерминации и корреляции характеризуют совместное влияние всех факторов на результат.

По аналогии с парной регрессией можно определить долю вариации результата, объясненной вариацией вклю­ченных в модель факторов , в его общей вариации . Ее количественная характеристика - теоретический множественный коэффициент детерминации . Для линейного уравнения регрессии данный показатель может быть рассчитан через β-коэффициенты, как:

.

- коэффициент множественной корреляции. Он принимает значения от 0 до 1 (в отличие от парного коэффициента корреляции, который может принимать отрицательные значения, R используется без учета на­правления связи). Чем плотнее фактические значения располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина . Таким образом, при значении R близком к 1, урав­нение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении R близком к 0 уравнение регрессии плохо описывает фактиче­ские данные и факторы оказывают слабое воздействие на результат.

Оценка значимости полученного уравнения множест­венной регрессии.

Оценка значимости уравнения множественной регрес­сии осуществляется путем проверки гипотезы: (гипотеза о незначимости уравнения регрессии).

Для ее проверки используют F-критерий Фишера.

При этом вычисляют фактическое (наблюдаемое) зна­чение F-критерия:

,

где n-число наблюдений; k - число независимых переменных модели.

По таблицам распределения Фишера находят критическое значение F-критерия . Для этого за­даются уровнем значимости (обычно его берут равным 0,05) и двумя числами степеней свободы и . Здесь m – число параметров модели.

Сравнивают фактическое значение F-критерия с табличным . Если , то гипотезу о незначимости уравнения регрессии не отвергают. Если , то выдвинутую гипотезу отвер­гают и принимают альтернативную гипотезу о статистиче­ской значимости уравнения регрессии.

Пример 2.

На основе данных, приведенных в Приложении и соответст­вующих варианту 100, требуется:

1. Построить уравнение множественной регрессии. Для этого, ос­тавив признак-результат тем же выбрать несколько признаков-факторов из приложения 1 (границы их наблюдения должны совпадать с границами наблюдения признака-результата, соот­ветствующих Вашему варианту). При выборе факторов нужно руководствоваться как экономическим содержанием, так и формальными подходами (например, матрица парных коэффи­циентов корреляции). Пояснить смысл параметров уравнения.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии (β-коэффициенты).

4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.

6. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

Решение:

По условию задачи, результативный признак должен остаться тот же, значит Y - дивиденды, начисленные по результатам деятельности. В качестве факторных признаков выберем следующие:

– балансовая прибыль;

- дебиторская задолженность по результатам деятельности.

Определим уравнение регрессии следующего вида:

Для определения параметров уравнения связи, а также для дальнейших расчетов построим дополнительную таблицу. (Таблица 2)

Для определения параметров двухфакторного уравнения регрессии необходимо решить систему нормальных уравнений:

В нашем случае система нормальных уравнений примет вид:

В результате решения данной системы получим следующие коэффициенты регрессии:

Окончательное уравнение регрессии примет вид:

.

При отсутствии влияния со стороны факторных признаков, учтенных в данной модели, значение результативного признака будет составлять 17,2714 млн. руб. При изменении балансовой прибыли на 1 млн. руб. произойдет изменение начисленных дивидендов в ту же сторону на 0,02645 млн. руб., а при изменении дебиторской задолженности на 1 млн. руб. следует ожидать изменения величины начисленных дивидендов на 0,00054 млн. руб.

Определим частные коэффициенты эластичности:

,

.

Частные коэффициенты эластичности показывают влияние отдельных факторов на результативный показатель. Так, при изменении балансовой прибыли на 1% при неизменности второго фактора произойдет в среднем изменение величины начисленных дивидендов на 0,14%, а при изменении дебиторской задолженности на 1% при фиксированном положении первого фактора произойдет изменение величины начисленных дивидендов в среднем на 0,0014%.

Теперь рассчитаем β-коэффициенты:

Анализ β-коэффициентов показывает, что на величину начисленных дивидендов из двух исследуемых факторов с учетом уровня их вариации большее влияние оказывает балансовая прибыль .

С учетом всех рассчитанных показателей и параметров уравнения регрессии можно сделать вывод о том, что наибольшая связь величины начисленных дивидендов отмечается с размером балансовой прибыли.

Далее, определим парные, частные коэффициенты корреляции и множественный коэффициент корреляции.

1. Парные коэффициенты корреляции: измеряют тесноту связи между двумя из рассматриваемых признаков.

,

,

.

Коэффициент корреляции между факторными признаками, равный -0,683, позволяет оставить в модели оба фактора, так как связь между факторами не тесная .

2. Частные коэффициенты корреляции: характеризуют степень влияния одного из факторов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне.

= ,

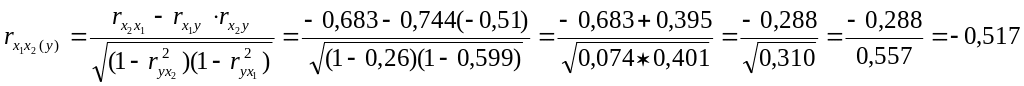
Таблица 2 - Дополнительная таблица

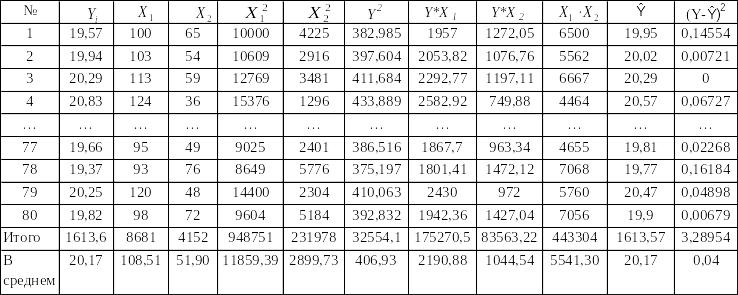
Близкая к тесной прямая связь результативного признака наблюдается с балансовой прибылью (0,677), практически отсутствует связь между начисленными дивидендами и дебиторской задолженностью (0,164).

3. Множественный коэффициент корреляции: показывает тесноту связи между результативным и обоими факторными признаками.

Таким образом, выявлена тесная связь между начисленными дивидендами и следующими признаками: балансовая прибыль и дебиторская задолженность.

Множественный коэффициент детерминации определим как квадрат множественного коэффициента корреляции:

.

На основе коэффициента детерминации делаем вывод, что на вариации величины начисленных дивидендов находится в зависимости от изменения балансовой прибыли и суммы дебиторской задолженности, и на – влиянием прочих неучтенных в модели факторов.

На завершительном этапе анализа проверим значимость параметров уравнения регрессии и модели в целом.

Проверим значимость модели в целом с помощью F-статистики Фишера. Для этого определим остаточную дисперсию результативного признака:

,

Тогда

= 57,51

,

, следовательно, модель в целом признается значимой.