2 Расчетная часть
2.1 Математическая обработка результатов прямых измерений
Выполнены измерения содержания азота в пробе чугуна. Получены следующие результаты: 0,0078 0,0082 0,0076 0,0075 0,0072 0,0095.
По ГОСТ 22536.1-77 методы определения содержания общего азота в интервале 0,006-0,0115 допускаемые расхождения в результатах параллельных определений Δp = 0,0010. Вычислить оценку истинного значения содержания азота в пробе чугуна.
Решение:
1. Расположим результаты измерений в возрастающей последовательности:
0,0072 0,0075 0,0076 0,0078 0,0082 0,0095
0.0010 = 0.0010
В интервал 0,0072 - 0,0082 попадает пять результатов из шести. Результат 0,0095, как содержащий грубую погрешность или промах, может быть отброшен из дальнейшего анализа.
2. Среднее арифметическое результатов измерений:
∑X = 0,0072+0,0075+0,0076+0,0078+0,0082 = 0, 383
=
0,383/5 = 0,00766.
3. Поскольку доверительная погрешность известна, можно сразу записать интервальную оценку.
δp = Δp / 2 = 0.0010/2 = 0.0005
[N] =0,00766+0.0005% Р = 0.9995 n=5
Доверительный интервал 0,00716+0,00816 с доверительной вероятностью Р = 0.9995 накрывает истинное значение измеряемого параметра.
2. 2 Математическая обработка результатов косвенных измерений
Составлена электрическая цепь (рисунок 2):
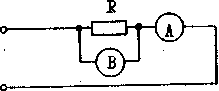
Рисунок 2 – электрическая цепь
Выполнены измерения тока в цепи с помощью амперметра А и напряжения на резисторе R с помощью вольтметра В и получены следующие результаты:
I, A |
0,45 0,47 0,46 0,45 0,47 |
U, B |
15,0 15,2 14,7 14,8 15,2 15,1 14,9 |
Используя закон Ома, определить интервальную оценку сопротивления резистора R.
Решение:
Математическая обработка результатов прямых измерений.
Введем обозначения: I-Х, U-Y, R-Z
а) ∑X = 2,3 ∑X2 = 1,0584 nx=5
= 2,3/5= 0,46
Р=0,95 ч.с.с.=5-1=4 t∙0,95=2,7764
I
=0,46
0,012
при Р=0,95
б) ∑Y = 104,9 ∑Y2 = 1572,23 n = 7
=
104,9/7=15,0
P=0,095 ч.с.с.=7-1=6 t ∙ 0,95=2,4469
U =15,0 0,18 при Р=0,95.
2
3 Частные погрешности результатов косвенных измерений:
4
5
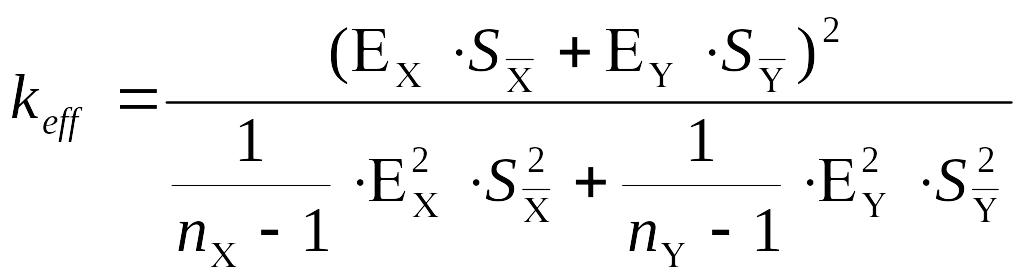
6 При доверительной вероятности Р = 0,95 табличные значения критерия Стьюдента:
ч.с.с. 6 7
t∙ 0,95 2,4469 2,3646
интерполяцией определяется: при keff = 6,75, t ∙0,95 = 2,3852,
7 R = 32,58 ± 0,18.
Доверительный
интервал 32,40
32,76
накрывает с доверительной вероятностью
Р=0,95 истинное значение искомого параметра.
2.3 Математическая обработка результатов совокупных и совместных измерений
Экспрессный способ определения содержания углерода в металле основан на зависимости концентрации этого компонента от температуры кристаллизации расплава. С целью установления зависимости между названными параметрами выполнены совместные измерения температуры ликвидус и содержания углерода и получены следующие результаты:
|
tл, оС |
0,98 |
1455 |
0,83 |
1470 |
0,74 |
1475 |
0,60 |
1488 |
0,51 |
1495 |
0,40 |
1504 |
0,36 |
1508 |
0,27 |
1517 |
0,13 |
1527 |
0,04 |
1535 |
%
С целью выяснения вида искомой зависимости между величинами экспериментальные данные представлены графически на рисунке 3.
Концентрация углерода в металле линейно изменяется с изменением величины t. Порядок величин [C]и t различен. С целью облегчения процесса вычисления приведем их к одному порядку путем введения новых переменных:
Y= [C], X = t/1000. Эта операция не приведет к искажению результатов и в то же время облегчит вычислительный процесс. Вместе с тем надо отметить, что округление промежуточных результатов при использовании метода наименьших квадратов не допустимо, так как может привести к искажению конечного результата.
Вид уравнения будет следующий:
Y=A1∙X+A2.
Как отмечено выше, пункты 3 4 можно не выполнять.
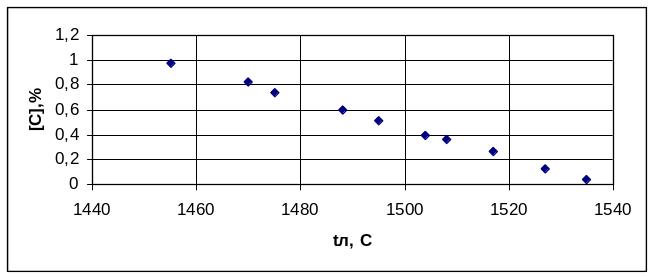
Рисунок 3 - Влияние температуры металла на концентрацию углерода
5.
После преобразования имеем:
Вычисляются необходимые суммы:
∑X(i)=14,9740
∑(X(i))2=22,4280
∑Y(i)∙X(i)=7,2067
∑Y(i)=4,8600
22,4280∙а1+14,9740∙а2=7,2067
14,9740∙а1+10∙а2 =4,8600
а1= - 0,7063/0,0597 = -11,8228
а2= 1,0867/0,0597= 18,1894
Таким образом, получается искомое уравнение:
Y= -11,8228∙X+18,1894
Для контроля правильности вычислений целесообразно в уравнение подставить средние значения , тогда в левой части должно получиться среднее значение . В данном случае =1,4974 и =0,4860.
Подставляя эти значения в равнение, получим:
0,4860= -11,8228∙1,497418,1894=0,4860,
т.е. получена удовлетворительная сходимость результатов.
6.Вычисляются остаточные погрешности условных уровней
|
|
|
|
0,9873 |
0,9800 |
0,0073 |
0,0001 |
0,8099 |
0,83 |
-0,0201 |
0,0004 |
0,7508 |
0,7400 |
0,0108 |
0,0000 |
0,5971 |
0,6000 |
-0,0029 |
0,0000 |
0,5144 |
0,5100 |
0,0044 |
0,0001 |
0,4080 |
0,4000 |
0,0080 |
0,0000 |
0,3607 |
0,36 |
0,0007 |
0,0001 |
0,2543 |
0,27 |
-0,0157 |
0,0002 |
0,1360 |
0,13 |
0,0060 |
0,0000 |
0,415 |
0,04 |
0,0015 |
0,0000 |
∑v12=0,0009.
7. S12=0,0009/(10-2)=0,0001
8.
Sa1=0,271
Sa2=0,211
9. t∙0,95=2,3060 при ч.с.с.=10-2=8
10.
А1= - 11,823 ± 0,325
А2= 18,189 ± 0,487
Переходя к исходным величинам, получим:
[C]=(18,189±0,325)-(11,823±0,487)∙t/1000