17. Нахождение длины векторов и угла между векторами через координаты векторов.

Формула для нахождения длины вектора а=(a₁a₂) по координатам на плоскости имеет вид |a|= а₁²+а₂²

Если на плоскости заданы точки А(a_x? a_y) и B(b_x, b_y), то вектор АВ имеет координаты (b_x-a_x,b_y-a_y), и его длина вычисляется по формуле |AB| = (b_x-a_x)²+( b_y-a_y)²

Углом между векторами a и b называется угол между лучами OA и OB.

Формула для нахождения косинуса угла между ненулевыми векторами

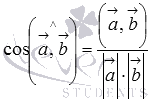
Формула для вычисления косинуса угла между векторами a=(a_x,a_y), b=(b_x,b_y), на плоскости имеет вид

18. Прямая на плоскости. Нормальный вектор к прямой.

Общее уравнение : Ax+By+C=0

Вектор N=(A,B) –нормальный вектор прямой

Частные случаи :

1. By+C=0 - прямая параллельна оси Ox

2. Ax+C=0 – прямая параллельна оси Oy

3. Ax+By=0 – прямая проходит через начало координат

4. y=0 – ось Ox

5. x=0 – ось Oy

19. Различные формы уравнения прямой на плоскости.

1. Через 2 точки : =

2. Через точку параллельно заданному вектору :

3. Параметрическое уравнение прямой : x=lt+x₀

y=mt+y₀

где (x₀,y₀) – координаты точки, лежащие на прямой, (l,m) – координаты направляющего вектора прямой

4. Через точку перпендикулярно заданному вектору : Дана точка M₀(x₀,y₀,z₀) перпендикулярно вектору N(A,B,C), значит A(x-x₀)+B(y-y₀)+C(z-z₀)=0

20. Угол между прямыми.

21. Расстояние от точки до прямой.

Расстояние от точки M(x₀,y₀) до прямой Ax+By+Cz=0

d=

В пространстве та же формула, только +D

22. Общее уравнение плоскости в пространстве. Нормальный вектор к плоскости

Общее уравнение : Ax+By+Cz+D=0

Вектор N=(A,B,C) – нормальный вектор к плоскости

23. Уравнение плоскости через 3 заданные точки

|x-x₁ y-y₁ z-z₁|

|x₂-x₁ y₂-y₁ z₂-z₁|=0

|x₃-x₁ y₃-y₁ z₃-z₁|

24. Уравнение плоскости через точку перпендикулярно заданному вектору

25. Уравнение прямой в пространстве. Канонической и параметрическое уравнение.

- каноническое уравнение (пусть прямая проходит через точку M₁(x₁,y₁,z₁) параллельно вектору s={l,m,n})

x= x₁+tl ; y=y₁+tm ; z=z₁+tn – параметрическое уравнение

26. Уравнение прямой через 2 заданные точки.

M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂) = =

27. Уравнение прямой через точку перпендикулярно заданной плоскости

28. Функция. Область её определения. Сложные функции. График функции

Если каждому значению х множества Х (х Х) ставится в соответствии вполне определённое значение у множества У (у У), то говорят, что на множестве Х задана функция у=f(x)

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y=f(x) определена.

Если множество Х специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция y=f(x) вообще не имеет смысл.

Сложной функцией называется такая функция, для вычисления значений которой нужно произвести несколько простейших операций.

29. Основные простейшие функции. Понятие элементарной функции.

Элементарная функция – такая функция, для вычисления значений которой для некоторого аргумента требуется произвести или ряд арифметических операций или ряд операций с простейшими функциями.

30. Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = f(x)

Функция называется нечетной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = –f(x)

2.Периодичность

Функция f(x) называется периодической с периодом если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).

4. Экстремумы

Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х) f(Xmax).

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

31. Определение экстремумов функции.

Экстремум - максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х₀ выполняется неравенство f(x) f(x₀)

Необходимые условия экстремума :

1. Пусть функция у=f(x) имеет в точке х₀ экстремум и в этой точке существует производная, тогда она равна 0

2. Если на каком-то участке АВ производная всюду положительная, то на этом участке функция возрастает (монотонно возрастающая) и если функция монотонно возрастающая и производная во всех точках существует, то она неотрицательна

Точки не обязательно являются точками экстремума, если производная равна 0.

Все стационарные точки (где производная равна 0) и точки, где производная не существует являются точками, подозрительными на точки экстремума.

Достаточное условие экстремума : если при переходе через точку, подозрительную на экстремум, производная меняет знак, то эта точка является экстремумом.