
Сургутский государственный университет
кафедра экспериментальной физики.
Лабораторная работа № 5.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
МАЯТНИКА МАКСВЕЛЛА.
ЛАБОРАТОРНАЯ РАБОТА № 5.
Определение момента инерции маятника максвелла.
Цель работы : Изучение плоского движения твердого тела на примере маятника Максвелла; измерение момента инерции маятника Максвелла.
Теория
Нетрудно показать , что любое движения твердого тела (например, движение космонавта на тренировочных центрифугах и т.д) может быть представлено как наложение двух простых видов движения: поступательного и вращательного.
При поступательном движении все точки тела получают за одинаковые промежутки времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми.
При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
Представляет интерес сопоставление основных величин и формул механики вращающегося твердого тела и поступательного движения материальной точки. Для удобства такого сопоставления в таблице1 слева приведены величины и основные соотношения для поступательного движения, а справа- аналогичные для вращательного движения.
Таблица1
Поступательное движение |
Вращательное движение |
S-путь
m-масса тела
Основной закон динамики
Кинетическая энергия
|
-поворот
J-момент инерции N=J-момент импульса
Основной закон динамики
Кинетическая энергия
|
Из таблицы видно, что переход в соотношениях от поступательного движения к вращательному осуществляется заменой скорости - на угловую скорость , ускорения - на угловое ускорение и тд.
В данной работе рассматривается плоское движение, т.е. такое, при котором под действием внешних сил все точки тела перемещаются в параллельных плоскостях. Примером плоского движения может служить качение цилиндра по плоскости (рис.а)



 а)
Это движение можно представить
как
а)
Это движение можно представить
как
 сумму
двух движений - поступатель-
сумму
двух движений - поступатель-
 ного
со скоростью
и вращательно-
ного
со скоростью
и вращательно-
го с угловой скоростью на рисунке ось вращения проходит перпендикулярно плоскости чертежа.
Назвав систему отсчета, относительного которой мы рассматриваем сложное движение твердого тела, неподвижной, движение тела можно представить как вращение с угловой скоростью . В системе отсчета, которая движется относительно неподвижной системы поступательно со скоростью .
Таким образом , ускорение каждой точки тела складывается из ускорения поступательного движения и ускорения при вращении вокруг оси, проходящей через центр масс. Ускорение поступательного движения одинаково для всех точек тела и равно
 ,
(1)
,
(1)
где

-
результирующая всех внешних сил, а
 - масса тела. Направление ускорения
совпадает с направлением результирующей
- масса тела. Направление ускорения
совпадает с направлением результирующей
 .
Ускорение вращательного движения
.
Ускорение вращательного движения
 вокруг оси, проходящей через центр масс
тела, равно
вокруг оси, проходящей через центр масс
тела, равно
 (2)
(2)
где
 -
момент всех внешних сил относительно
оси, проходящей через центр масс тела,
а
-
момент всех внешних сил относительно
оси, проходящей через центр масс тела,
а
 -
момент инерции тела относительно той
же оси.
-
момент инерции тела относительно той
же оси.
В данной работе плоское движение тела изучается на примере движения маятника Максвелла.
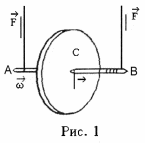
Составим уравнение поступательного движения маятника без учета сил трения о воздух (рис 1)
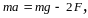 (3)
(3)
где
 и
и
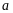 масса маятника и ускорение центра масс
соответственно g-ускорение
свободного падения, F-сила
натяжения нити.
масса маятника и ускорение центра масс
соответственно g-ускорение
свободного падения, F-сила
натяжения нити.
Уравнение вращательного движения для маятника имеет следующий вид
 (4)
(4)
 - радиус оси,
- радиус оси,
 -
сила натяжения одной нити.
-
сила натяжения одной нити.
Поступательное и вращательное ускорения связаны соотношением
 (5)
(5)
Поступательное
ускорение маятника можно определить,
измерив время опускания маятника
 и расстояние,
которое он проходит за это время
и расстояние,
которое он проходит за это время
 :
:
 (6)
(6)
Из уравнений (3), (4), (5) и (6) выразим момент инерции маятника Максвелла
 (7)
(7)
Теоретическое значение момента инерции маятника определяют по формуле
 (8)
(8)
где
 момент инерции оси маятника;
момент инерции оси маятника;
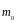 - масса оси
- масса оси
 - момент инерции
диска маятника;
- момент инерции
диска маятника;
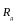 - внешний радиус диска,
- внешний радиус диска,
 - масса диска;
- масса диска;

-
момент инерции только сменного кольца;
 - внешний радиус кольца,
- внешний радиус кольца,
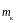 - масса кольца.
- масса кольца.

 -линейная
скорость
-линейная
скорость =
=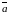 -линейное
ускорение
-линейное
ускорение -импульс
тела
-импульс
тела -сила
-сила

 -работа
-работа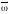 -угловая
скорость
-угловая
скорость =
=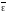 -угловое
ускорение
-угловое
ускорение -момент
силы
-момент
силы

 -работа
-работа