3.3. Оцінки параметрів рухливості структурних елементів макромолекул лінійних аморфних полімерів на основі фрактальних розмірностей

Для оцінки лінійних розмірів кластерів у роботі [49] пропонується розглядати поведінку фононного газу, який характеризується в’язкістю і часом релаксації τ:

. (3.41)

Проведені обчислення для цілого ряду полімерних систем дають значення від 0,2 нм до 0,4 нм. Для визначення розмірів міжкластерних областей вважається, що в області температур нижчих за температуру склування, процес утворення пустот («дірок») відбувається в областях розпушеного упакування елементів структури. Тоді співставлення лінійних розмірів міжкластерних областей об’єму дірки та розмірам ланки макромолекули флуктуаційного вільного об’єму , можна визначити лінійні розміри міжкластерних областей згідно із співвідношенням:

. (3.42)

Якщо виходити з трикомпонентної моделі аморфних полімерів, то при розгляді деформацій зсуву, які відбуваються по перехідних областях порядок-безпорядок, можна визначити лінійні розміри цих структуроутворень як:

, (3.43)

де - динамічна в’язкість, τ – час релаксації структуроутворення при деформаціях зсуву. Розрахунки показують, що величина міститься в межах 1,0–2,0 нм, а - 0,3–0,4нм. Таким чином аморфний полімер можна розглядати як сукупність наноструктур з лінійними розмірами , тобто кластер-перехідна область – міжкластерна область, із значною ймовірністю переходу структурних елементів із кластерних областей у міжкластерні і навпаки через перехідну межу.

Використання такої моделі для лінійних аморфних полімерів дає можливість вважати, що кластерні області вкраплені в розпушену полімерну матрицю (міжкластерні утворення). Такі уявлення на структурному рівні дозволяють розглядати лінійні аморфні полімери як нанокомпозити і використовувати мікрокомпозитні моделі для опису їх поведінки [50].

Для визначення відносної частки кластерів у ПВХ використаємо перколяційне співвідношення запропоноване в роботі [51]:

, (3.44)

де Т_ – температура склування. Для ПВХ Т_с=353 К [52].

На рис. 3.3 подана залежність від Т. Згідно цієї залежності частка кластерів зменшується із зростанням температури. Проте цей процес зумовлений не тільки переходом структурних елементів макромолекул із кластрених областей в міжкластерні, але й можливістю захоплення кластерами ділянок макромолекул, що призводить до зростання лінійних розмірів самих кластерів (крива 2, рис. 3.3).

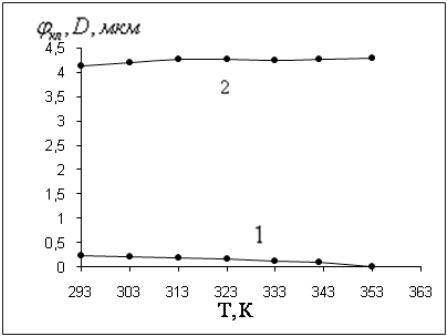
Рис. 3.3. Залежність (1) і D (2) від температури для ПВХ.

Згідно уявлень викладених у роботах [53, 54] кластери відіграють роль багатофункціональних вузлів сітки фізичних зв’язків, яку характеризують функціональністю кластера (F) (число вихідних полімерних ланцюгів). Функціональність кластера знаходиться за концепцією каучукової еластичності [55]:

, (3.45)

де – рівноважний модуль зсуву, V_кл – об’єм кластера, k – стала Больцмана.

Вважаючи кластер кульовим утворенням радіуса , отримаємо:

. (3.46)

На рис. 3.4 подана температурна залежність F. До того ж при обчисленні F вважали, що рівний динамічному модулю зсуву при відповідних температурах. Значення F дають можливість визначити число сегментів в одному кластері [56].

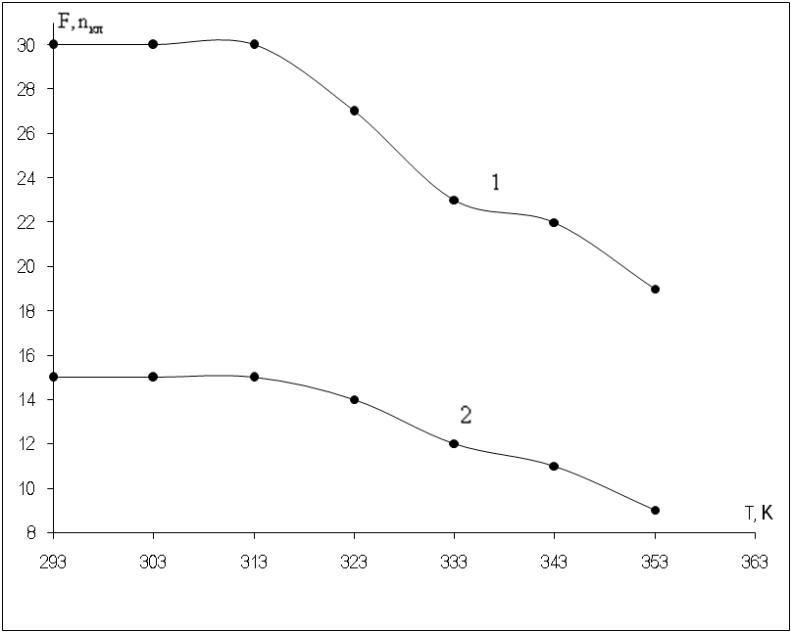
Рис. 3.4. Температурна залежність F (1) і n_кл (2) для ПВХ.

Аналіз залежностей F і n від Т вказує на те, що розпад кластерів стає помітним лише при температурі -переходу, яка для ПВХ складає 325-333 К [57, 58].

Використання мікрокомпозитних моделей та їх трактування для залежності ступеня підсилення [59] від об’ємного вмісту дають можливість оцінити модулі поздовжньої деформації і зсуву для розпушеної ділянки (міжкластерних областей). Для цього вважається, що модуль Е_к рівний модулю полімера, Е_матр – модулю міжкластерної області. В області температур склоподібного стану, як було показано в роботі [60], між кластерами та розпушеними областями спостерігається нулева адгезійна міцність при великому коефіцієнті тертя між наповнювачем та матрицею. Тоді модулі пружності міжкластерних областей визначаються як:

; (3.47)

.

У температурному інтервалі, що відповідає -переходу, ідеальна адгезія між нанонаповнювачем і матрицею описується рівнянням Кернера, із якого отримаємо, що:

(3.48)

Результати розрахунків динамічних модулів деформації полімера і міжкластерних областей в залежності від температури подали на рис. 3.5.

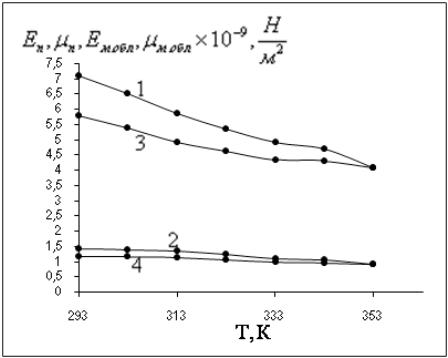
Рис. 3.5. Температурна залежність Е_п (1), _п (2) та Е_м.обл (3), _м.обл (4) для ПВХ.

Якщо вважати, згідно кластерної моделі, густину кластерів і міжкластерних областей однаковою і рівною густині ПВХ, то значення модулів поздовжньої та деформації зсуву дозволяє визначити швидкості поширення ультразвукових хвиль у міжкластерних областях. Для їх визначення використаємо співвідношення:

; . (3.49)

Значення швидкості поширення поздовжніх і поперечних звукових хвиль дають можливість визначити коефіцієнт Пуассона і параметр Грюнайзена як для самого полімера так і розпушеної ділянки. Коефіцієнт Пуассона визначається згідно співвідношення (3.2) або за рівнянням:

, (3.50)

а решітковий параметр Грюнайзена як:

. (3.51)

Згідно підходу запропонованого в роботі [61], решітковий параметр Грюнайзена визначається як , де – середня швидкість фононів в системі, а V – питомий об’єм.

Результати розрахунків  та _l для міжкластерних областей подані в таблиці 3.2.

Таблиця 3.2.

Температурна залежність в’язкопружних властивостей і фрактальних вимірностей для розпушених областей ПВХ

Т, К	293	303	313	323	333	343	353
, м/с	2080	2010	1930	1880	1850	1840	1810
, м/с	930	930	930	900	870	870	850
	0,38	0,37	0,35	0,35	0,36	0,36	0,35
l	5,75	5,27	4,5	4,5	4,9	4,9	4,5
df	2,78	2,74	2,70	2,70	2,72	2,72	2,70

За значеннями  та _l визначали фрактальну вимірність структуроутворень ПВХ [62]:

, (3.52)

або

, (3.53)

де d – евклідова вимірність простору.

Фрактальна вимірність d_f, дає можливість проаналізувати рухливість ділянок макромолекул, як в кластерах так і в міжкластерних областях, яка зумовлена дією температурного поля. На основі значень d_f визначали фрактальну вимірність рухливості ділянок полімерного ланцюга згідно [63]:

, (3.54)

n_c – кількість статистичних сегментів, що відповідає цій ділянці.

Якщо вважати, що n_c = n_кл, то фрактальна вимірність самого кластера рівна:

. (3.55)

Результати розрахунків величини d_Д подані в таблиці 3.3. Аналіз температурної залежності цієї величини вказує на те, що в області -переходу фрактальна вимірність d_Д зменшується, за рахунок послаблення міжмолекулярної взаємодії між сегментами сусідніх ділянок макромолекул. Значення n_кл дають можливість визначити довжину ділянки між защемленнями кластерів, як:

, (3.56)

де  – енергетична жорсткість макромолекул ПВХ, l₀ – довжина реального зв’язку скелетного ланцюга.

Таблиця 3.3.

Температурна залежність мікроструктур них параметрів і фрактальних вимірностей для ПВХ

Т, К	293	303	313	323	333	343	353
	0,37	0,36	0,35	0,35	0,36	0,35	0,35
l	5,27	4,9	4,5	4,5	4,9	4,5	4,5
df	2,74	2,72	2,70	2,70	2,72	2,70	2,70
dД	1,72	1,78	1,84	1,74	1,69	1,63	1,57
	1,42	1,40	1,38	1,36	1,33	1,30	1,27
Lc, мкм (спів. 3.56)	33,06	32,24	31,52	29,47	24,38	21,82	19,53
Lc, мкм (спів. 3.57)	33,80	32,34	31,88	29,32	24,57	22,02	19,56

Енергетичну жорсткість макромолекул ПВХ визначали згідно підходів запропонованих у роботах [64, 65] і температурна залежність  подана в таблиці 3.3. За іншим підходом значення L_c можна визначити на основі значень d_f і d_Д як [66]:

. (3.57)

Порівняння цих значень обчислених на основі співвідношень (3.56) і (3.57) показують, що вони близькі між собою, а аналіз температурної залежності засвідчує зменшення L_c з ростом Т. Такий характер залежності L_c вказує не тільки на зменшення енергетичної жорсткості структурних елементів макромолекул ПВХ, але й збільшення ймовірності руйнування кластерів при зростанні температури.

Наноструктурний підхід до опису морфологічних особливостей лінійних аморфних полімерів вказує на те, що вони є самоподібними, а тому процеси рухливості структурних елементів макромолекул ПВХ, як в кластерах так і в розпушених областях, проаналізуємо в рамках теорії самоподібних стохастичних систем [67, 68]. Відповідно до неї коефіцієнт дифузії структурних елементів макромолекул ПВХ визначається як:

. (3.58)

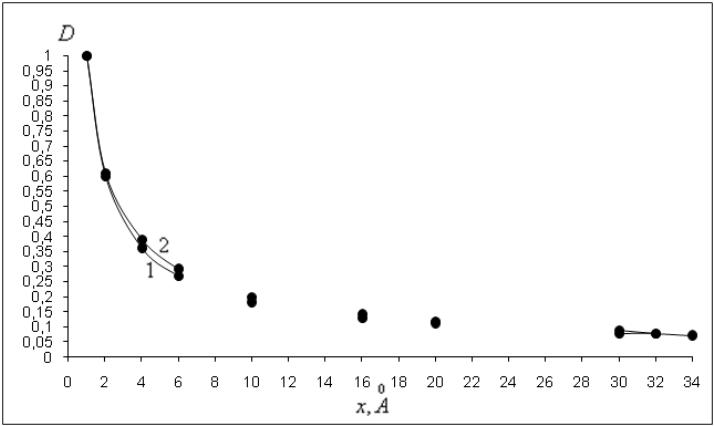
Рис. 3.6. Залежність коефіцієнта дифузії від лінійних розмірів структурних елементів макромолекул з показниками -0,74 (1); -0,70 (2)

Аналіз цих залежностей (рис. 3.6) показує, що в межах кластерів, коли довжина структурних одиниць незначна (1,5–2 ) коефіцієнт дифузії для них значний і зростає в температурному діапазоні  і -переходів. Аналогічна картина спостерігається і для таких же структурних елементів, що перебувають в міжкластерних областях. Коефіцієнт дифузії для сегментів макромолекул, що перебувають в кластерах і міжкластерних областях, зменшується тобто рухливість самих наноструктурних утворень утруднена. Рухливість об’єднання кластерів, як єдиного цілого (x = L_c) дуже утруднена в розпушеній матриці. Зростання температури не зумовлює зростання рухливості таких структуроутворень, хоч і їх лінійні розміри змінюються.