2.3. Ультразвукові та теплофізичні експериментальні методи досліджень властивостей аморфних полімерів та їх систем

У дослідженні будови полімерних матеріалів та їх фізичних властивостей важливе значення набувають ультразвукові методи, які базуються на вимірюванні швидкостей поширення і поглинання пружних хвиль [34]. Перевага ультразвукових методів полягає в тому, що вони дозволяють досліджувати силове поле молекул, динаміку руху кінетичних одиниць, отримати інформацію про внутрішню структуру матеріалу без його руйнування [34].

Дослідження механічних динамічних характеристик ПКМ повязане з вимірюванням швидкостей поширення поздовжньої ( ) та поперечної ( ) ультразвукових хвиль та відповідних коефіцієнтів їх затухання (_l, _t).

Робота експериментальної ультразвукової установки, яка працює на частоті 0,4 МГц, ґрунтується на імпульсному методі з прохідним сигналом у поєднанні з методом обертової пластини.

Розроблена [34] експериментальна установка за один прийом дозволяє за допомогою диференціальної кювети в області температур, обмежених точкою Кюрі п’єзоперетворювачів, визначити поздовжню і поперечну швидкості поширення пружних хвиль, а також коефіцієнти їх поглинання.

Швидкість поширення поздовжньої хвилі у зразку розраховувалася за співвідношенням :

(2.1)

Швидкість поширення поперечної хвилі у зразку визначали методом оборотної пластини і розраховували за наступним співвідношенням:

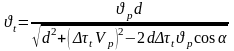, (2.2)

де d – товщина зразка; 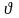_p – швидкість поширення ультразвукової хвилі в імерсійній рідині при температурі дослідження; _l,t – час проходження ультразвукового сигналу через досліджуваний зразок, виміряний вимірником часових інтервалів;  – кут повороту зразка.

На основі математичної обробки результатів проведених експериментів відносні похибки вимірювання в’язкопружних властивостей композицій складають:

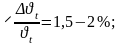
Густина () ПКМ вимірювалася ділатометричним методом, в основу якого покладено метод гідростатичного зважування (відносна похибка вимірювань густини _=0,03 % при =0,95).

Розроблений автоматичний комплекс для широкотемпературних вимірювань теплофізичних величин ПКМ на базі серійних установок типу ”ИТ-С-400”(ГОСТ 8.001-71) та ”ИТ--400”(ГОСТ 8.001-80), в основу принципу роботи яких покладено метод монотонного нагріву зразка, дозволив дослідити температурні залежності питомої теплоємності (с_р) та теплопровідності () композицій при контролі температури з точністю _Т=0,1%. Похибка вимірювань с_р не перевищує 1 %,  – 3 % при =0,95 у всьому робочому діапазоні температур.

Розділ ііі. Фрактальні розмірності полівінілхлоридних систем та процеси структуроутворення в них

3.1. Коефіцієнт Пуассона лінійних аморфних полімерів та їх систем

При розгляді коливальних процесів у гетерогенних полімерних системах, вважалося, що взаємодія між структурними елементами описується гармонічним наближенням. Проте в більшості випадків у таких системах крім гармонічних ефектів знаходять прояв і ангармонічні. Для характеристики перших ефектів використовують коефіцієнт Пуассона, який є параметром лінійної теорії пружності, а для характеристики відхилення від лінійності сил взаємодії між структурними елементами макромолекул застосовують параметр Грюнайзена. Коефіцієнт Пуассона характеризує зміну об’єму системи при одноосній деформації:

(3.1)

і може змінюватися в межах [35] –1 <  < 0,5. До того ж, слід зауважити, що коефіцієнт Пуассона є структурно більш чутливою характеристикою в порівнянні з пружними модулями [36].

Якщо відомі швидкості поширення поздовжніх і поперечних ультразвукових хвиль у гетерогенних полімерних системах, значення коефіцієнта Пуассона знаходять як [37]:

(3.2)

З іншого боку коефіцієнт Пуассона можна виразити через обємний модуль пружності і модуль зсуву згідно співвідношення [38]:

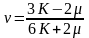(3.3)

Використавши значення і , а також значення К і  провели обчислення коефіцієнта Пуассона для полімерних систем. Як показують результати розрахунків, згідно співвідношення (3.2) виконані для вихідних ПВХ і ПВБ значення  складають 0,36 і 0,37. При проведенні розрахунків згідно співвідношення (3.3) значення  рівні 0,38, що співпадає з значенням коефіцієнта Пуассона отриманого в роботі [39] близькі за значенням , обчисленими згідно виразу 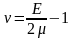, за результатами експериментальних досліджень статичних модулів. При порівнянні відповідних значень  для ПВХ, ПВБ з іншими полімерами можна вказати на те, що в ПВХ полярні бокові групи забезпечують достатньо ефективну молекулярну взаємодію. Також ефективна взаємодія характерна і для громіздких бокових груп ПВБ, оскільки коефіцієнт Пуассона для даного полімеру близький до значень  ПВХ.

Дослідження концентраційної залежності  для полімерних систем наповнених мінеральними наповнювачами (таблиця 3.1) показує, що в області малого вмісту (  2 об.%) інгредієнтів значення коефіцієнта Пуассона для таких систем перевищує відповідні значення  для вихідного полімера. Такий характер залежності  від  знаходить своє пояснення в рамках концепції впливу незначних часток наповнювача на процеси формування структури гетерогенних полімерних систем. При введені незначної частки наповнювача зростає вміст межового шару, коли розглядати наповнені полімерні системи як трьохкомпонентні: полімерна матриця – межовий шар – наповнювач. Такий підхід дозволяє розглядати полімерну систему, як таку в якій ніяких структурних змін не відбувається в порівнянні з вихідним полімером. Введення перших часток наповнювача приводить до зростання вмісту межового шару в системі від 5,4 об.% при  = 0,1 об.% ФГ_Pb до 10,8 об.% при  =  = 2 об.% ФГ_Pb, і відповідно від 9,9 об. % при  = 0,1 об.% ФГ_Hg до 15,3 об.% при  = 2 об.% ФГ_Hg і 10,7 об.% при  = 0,1 об.% ФГ_Bi до 17,4 об.% при  = 2 об.% ФГ_Ві [40]. Для систем наповнених ФГ відповідно значення концентрації межового шару складають 8,7 об.% при  = 0,1 об.% до 28,2 об.% при  = 2 об.% ФГ. Як видно з наведених даних в області концентрацій наповнювача 0 – 2 об.% обємний вміст межового шару в системі інтенсивно зростає, що зумовлює процеси переносу структурних елементів з полімерної матриці в межовий шар. Процес переходу структурних елементів приводить до зростання їх інтенсивності руху, а відповідно до сильнішого прояву нелінійності міжатомних сил як між самими структурними елементами макромолекул вихідних полімерів, так і тими структурними елементами макромолекул, які взаємодіють з поверхнею наповнювача.

Таблиця 3.1

Коефіцієнт Пуассона, параметр Грюнайзена, структурні характеристики ПВХ – систем при Т = 293 К

 об.%	 (спів. 3.2)	 (спів. 3.3)	Евзаєм. 10-20, Дж	Рвн, МПа	Екоггез., кДж/моль	m2	В
ПВХ + ФГ
0,1	0,37	0,38	1,755	229	10,573	5,3	0,10
0,5	0,37	0,38	1,942	254	11,694	5,3	0,09
1,0	0,36	0,37	1,995	263	12,021	4,9	0,11
2,0	0,36	0,37	2,027	272	12,212	4,9	0,13
3,0	0,35	0,36	2,120	289	12,772	44,5	0,10
5,0	0,35	0,36	2,163	301	13,027	4,5	0,10
10,0	0,33	0,33	2,130	315	12,834	3,9	0,11
20,0	0,33	0,33	2,005	333	12,079	3,9	0,10
ПВХ + ФГHg
0,1	0,37	0,38	1,786	232	10,761	5,3	0,10
0,5	0,36	0,37	1,758	230	10,589	4,9	0,10
1,0	0,34	0,35	1,992	261	12,000	4,2	0,11
2,0	0,36	0,37	1,870	250	11,265	4,9	0,10
3,0	0,36	0,37	1,937	263	11,665	4,9	0,10
5,0	0,34	0,34	2,090	289	12,590	4,2	0,11
10,0	0,34	0,34	2,054	298	12,374	4,2	0,12
20,0	0,33	0,33	2,072	325	12,483	3,9	0,12
ПВХ + ФГPb
0,1	0,37	0,38	1,841	239	11,068	5,3	0,10
0,5	0,37	0,38	1,728	227	10,406	5,3	0,09
1,0	0,37	0,38	1,737	228	10,464	5,3	0,09
2,0	0,37	0,38	1,728	231	10,409	5,3	0,09
3,0	0,36	0,37	1,870	254	11,266	4,9	0,10
5,0	0,36	0,37	1,989	275	11,979	4,9	0,10
10,0	0,35	0,36	2,247	326	13,537	4,5	0,11
20,0	0,33	0,34	2,665	418	16,056	4,9	0,12
ПВХ + ФГBi
0,1	0,37	0,38	1,824	237	10,991	5,3	0,09
0,5	0,37	0,38	1,728	227	10,413	5,3	0,09
1,0	0,36	0,37	1,844	242	11,105	4,9	0,10
2,0	0,37	0,38	1,810	242	10,904	5,3	0,09
3,0	0,36	0,37	1,892	257	11,397	4,2	0,10
5,0	0,34	0,34	2,068	286	12,457	4,2	0,11
10,0	0,33	0,34	2,316	336	13,952	3,9	0,12
20,0	0,30	0,31	2,436	382	14,673	3,3	0,13

У більшій мірі проявляються лінійні ефекти при реалізації міжмолекулярної взаємодії ( зменшення коефіцієнту Пуассона ) при зростанні частки наповнювача в полімерних системах. Зростання концентрації наповнювача приводить до того, що частка полімеру, який переходить у межовий шар, зростає менш інтенсивно. Так при  = 10 об.% частка межового шару для ФГ_Pb становить 16,8 об.%, ФГ_Ві – 21,0 об.%, ФГ_Hg – 18,9 об.%, ФГ – 4,5 об.% і прямує до насичення. Перерозподіл структурних елементів між областями матриця – межовий шар приводить до сповільнення релаксаційних процесів, а отже зменшення рухливості структурних елементів макромолекул.

Рис. 3.1. Температурна залежність величини  для систем:1 – ПВХ; 2 – ПВХ+3,0 об.%ФГ

Як видно з рис. 3.1 для вихідного ПВХ, полімер-полімерних систем, полімерних систем наповнених мінеральним наповнювачем ріст температури зумовлює незначне підвищення . Найбільш істотні зміни коефіцієнта Пуассона спостерігаються при досягненні температури склування для даних систем. Слід зауважити, що у всьому розглянутому діапазоні температур  полімер-полімерних систем має найбільші значення, для систем ПВХ + 3 об.% ФГ значення коефіцієнта Пуассона найнижчі. Зміни значень  від Т зумовлені тим, що при зростанні температури збільшується амплітуда коливань структурних елементів і зростає доля флуктуаційного вільного об’єму. Підтвердженням того, що зростає амплітуда теплових коливань структурних елементів, а отже посилюється ангармонізм міжмолекулярних взаємодій є взаємозв’язок коефіцієнта Пуассона з температурою Дебая 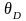. Якщо виходити з рівняння Грюнайзена [41]:

(3.4)

де  – коефіцієнт обємного розширення, – теплоємність,  – параметр Грюнайзена, що характеризує ангармонізм коливань решітки, то права частина цього рівняння виражає зв’язок з тепловими коливаннями структурних елементів у решітці. У свою чергу величина 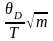, де m – маса структурного елементу, визначає величину середньоквадратичного зміщення від положення рівноваги. Вважаючи температуру Дебая, як функцію абсолютної температури отримали графічно залежність від (рис.3.2), яка є фактично лінійною функцією такий характер залежності вказує на зростання середньоквадратичного зміщення при зростанні температури системи.

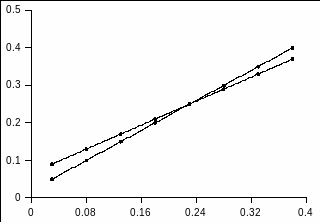
Рис. 3.2. Залежність величини для ПВХ (1), ПВХ+3 об.%ФГ (2)