
- •Дифференциальное исчисление глава: производная функция
- •Задача о нахождении скорости движения
- •Определение производной. Ее механический и геометрический смысл.
- •Найти производную функции , где
- •Механический смысл производной
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Связь между непрерывностью и дифференцируемостью
- •Производная суммы, разности, произведения и частного функций
- •Производная сложной функции
- •Практические задачи:
- •Производные основных элементарных функций
- •Производные высших порядков
- •Механический смысл производной второго порядка
- •Дифференциал функции понятие дифференциала
- •Основные теоремы о дифференциалах
- •Дифференциал сложной функции
- •Правила Лопиталя
- •Примеры:
- •Раскрытие неопределенностей различных видов
- •Исследование функций при помощи производных
- •П. Максимум и минимум функций
- •П. Наибольшее и наименьшее значения функции на отрезке
- •Замечания:
- •П. Выпуклость, вогнутость графика функции. Точки перегиба
- •П. Асимптоты графика функции
- •Общая схема исследования функции и построения графика
П. Выпуклость, вогнутость графика функции. Точки перегиба
ОПРЕДЕЛЕНИЕ: График дифференцируемой функции называется выпуклым в интервале , если он расположен, ниже касательной, проведенной в любой точке этого интервала.
ОПРЕДЕЛЕНИЕ: График дифференцируемой функции называется вогнутым в интервале , если он расположен выше касательной, проведенной в любой точке этого интервала.
ТЕОРЕМА:
(ДОСТАТОЧНОЕ
УСЛОВИЕ ВЫПУКЛОСТИ, ВОГНУТОСТИ ГРАФИКА
ФУНКЦИИ). Если
функция
во всех точках интервала
имеет
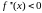 ,
то график функции является выпуклым,
если
,
то график функции является выпуклым,
если
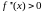 для
для
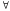 ,
то график является вогнутым.
,
то график является вогнутым.
ОПРЕДЕЛЕНИЕ: Точки, в которых вторая производная не существует или рана нулю, называются критическими точками 2 рода.
Для нахождения точек перегиба графика функции используется следующая теорема.
ТЕОРЕМА:
Если вторая производная при переходе
через критическую точку 2 рода
,
в которой она равна нулю
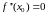 (или не существует), меняет знак, то
точка
-
есть точка перегиба.
(или не существует), меняет знак, то
точка
-
есть точка перегиба.
ПРИМЕР:
Исследовать на выпуклость, вогнутость
и точки перегиба функцию
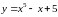
РЕШЕНИЕ:
Найдем
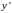 и
и
 ,
,
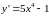 ,
,
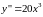
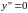 только при
только при
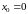 на интервале
на интервале
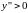 при
при
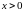 и
и
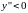 при
при
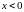 ,
следовательно, график функции в интервале
,
следовательно, график функции в интервале
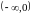 выпуклый, а
выпуклый, а
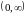 - вогнутый.
- вогнутый.
В
точке
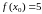 и точка
и точка
 -
точка перегиба.
-
точка перегиба.
П. Асимптоты графика функции
Построение графика функции облегчается, если знать его асимптоты.
ОПРЕДЕЛЕНИЕ: Асимптотой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят,
что прямая
является вертикальной
асимптотой
графика функции
,
если
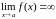 ,
или
,
или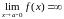 ,
или
,
или
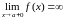
Действительно,
в этом случае из рисунка видно, что
расстояние от точки
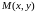 кривой до прямой
равно
кривой до прямой
равно
 .
Если
.
Если
 ,
то
,
то
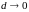 .
Согласно определению асимптоты
-
является асимптотой функции
.
.
Согласно определению асимптоты
-
является асимптотой функции
.
Для
отыскания вертикальных асимптот нужно
найти те значения
 ,
вблизи которых функция неограниченно
возрастает по модулю. Обычно это точки
разрыва 2 рода.
,
вблизи которых функция неограниченно
возрастает по модулю. Обычно это точки
разрыва 2 рода.
ПРИМЕР:
Функция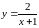 имеет вертикальную асимптоту
имеет вертикальную асимптоту
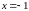 ,
т.к.
является точкой разрыва 2 рода:
,
т.к.
является точкой разрыва 2 рода:
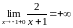 и
и
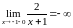
Уравнение наклонной асимптоты ищется в виде
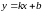 ,
,
Где
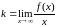 (1)
(1)
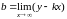 (2)
(2)
Если
хотя бы один из пределов не существует
или равен
 ,
то кривая
наклонных асимптот не имеет.
,
то кривая
наклонных асимптот не имеет.
В
частности: если
 ,
то
,
то
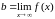 ,
поэтому
,
поэтому
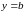 уравнение горизонтальной асимптоты.
уравнение горизонтальной асимптоты.
ЗАМЕЧАНИЕ:
Асимптоты
при
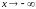 и при
и при
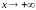 могут быть разными. Поэтому при нахождении
пределов (1) и (2) следует отдельно
рассматривать случай, когда
и
.
могут быть разными. Поэтому при нахождении
пределов (1) и (2) следует отдельно
рассматривать случай, когда
и
.
ПРИМЕР:
Найти асимптоты
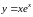
1)
 при
наклонной асимптоты не существует
при
наклонной асимптоты не существует
2)

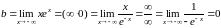 следовательно,
при
график функции имеет одну горизонтальную
асимптоту
следовательно,
при
график функции имеет одну горизонтальную
асимптоту
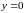
Общая схема исследования функции и построения графика
Найти область определения функции
Найти если это возможно точки пересечения графика с осями координат
Определить участки непрерывности, указать точки разрыва, если они есть и характер разрыва.
Найти интервалы знакопостоянства функции (промежутки на которых
 ,
,
 ).
).Выяснить является ли функция четной, нечетной или общего вида.
Найти асимптоты графика функции
Найти интервалы монотонности функции
Найти экстремумы функции
Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
Схема не является обязательной. В более простых случаях достаточно выполнить 3 пункта 1, 2, 7.
