П. Максимум и минимум функций

ОПРЕДЕЛЕНИЕ: Точка называется точкой максимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется

ОПРЕДЕЛЕНИЕ: Точка называется точкой минимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется

Значение функции в точке максимума называется максимумом функции

Значение функции в точке минимума называется минимумом функции

Максимум и минимум функции называются экстремумами функции.

ТЕОРЕМА (необходимое условие экстремума): Если дифференцируемая функция имеет экстремум в точке , то ее производная в этой точке равна нулю

Геометрически это значит: касательная в этой точке функции параллельна .

Обратная теорема НЕВЕРНА!

Если , то - не обязательно точка экстремума. Например: , , 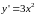при , но не точка экстремума!

ЗАМЕЧАНИЕ: Существуют функции, которые в точках экстремума не имеют производных. Например , при функция не дифференцируема, но точка минимума функции.

ТАКИМ ОБРАЗОМ: непрерывная функция может иметь экстремум лишь в точках, где производная или равна нулю или не существует.

Такие точки называются критическими точками первого рода

ОПРЕДЕЛЕНИЕ: Точки, в которых производная равна нулю, иногда называются стационарными.

ТЕОРЕМА (достаточное условие экстремума): Если непрерывная функция

дифференцируема в некоторой окрестности критической точки и при переходе через нее (слева направо), производная меняет свой знак с

« » на « », то - точка максимума

« » на « », то - точка минимума

Иногда бывает удобно использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

ТЕОРЕМА: Если в точке первая производная функции равна нулю , а вторая производная в точке существует и отлична от нуля , то при - в точке функция имеет максимум

при - в точке функция имеет минимум

П. Наибольшее и наименьшее значения функции на отрезке

Пусть функция непрерывна на отрезке . Известно, что по т. ВЕЙЕРШТРАССА такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке отрезка , либо на границе отрезка, т.е. при или . Если , то точку следует искать среди критических точек данной функции.

Получаем следующее правило нахождения наибольшего и наименьшего значений функции на :

1. Найти критические точки функции на интервале

2. Вычислить значения функции в найденных критических точках

3. Вычислить значения функции на концах отрезка, т.е. в точках и

4. Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Замечания:

1. Если функция на отрезке имеет 1 критическую точку и она является точкой максимума (или минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.

1. Если функция на отрезке не имеет критических точек, то это означает, что на нем функция монотонно возрастает (или убывает). Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, наименьшее – на другом.

ПРИМЕР: Найти наибольшее и наименьшее значения функции на отрезке .

РЕШЕНИЕ: Находим критические точки данной функции, для этого находим производную и смотрим, где она равна нулю или не существует

, при или .

; ; ;

ИТАК: в точке ; в точке