Курсовой проект(1)

1 Задание на курсовую работу

1.1 В данной работе исследуется установившийся и переходной режимы в электрической цепи (рис.1.1)

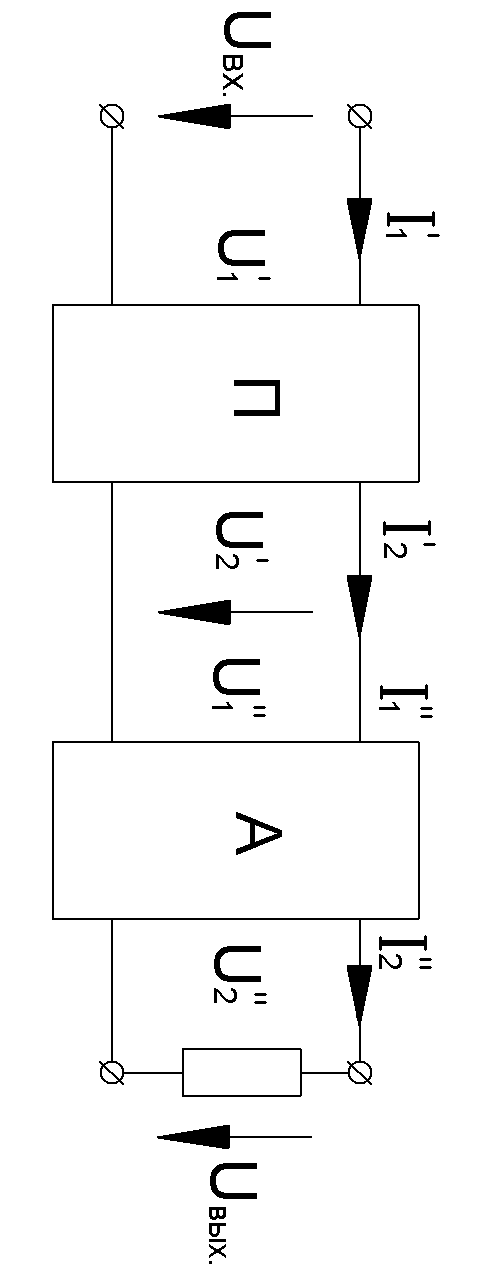
Рис.1.1 Схема соединения пассивного и активного четырёхполюсников

1.2 В соответствии с вариантом задания построить схемы пассивного четырёхполюсника П (рис.1.2), содержащего последовательное (Z) или параллельное (Y) соединение резистора и ёмкости (i=1,2,3) и

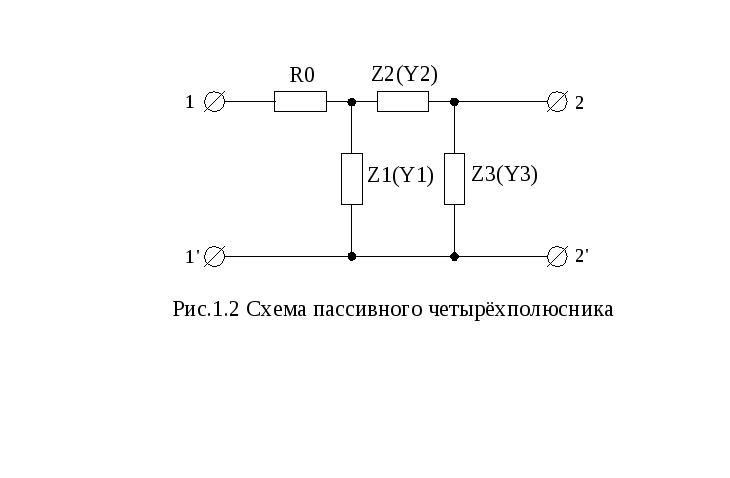
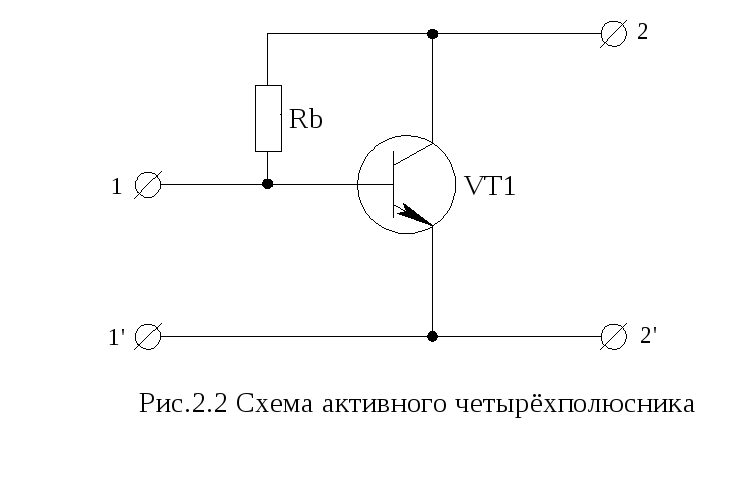
активного четырёхполюсника (рис.2.2).

1.3 Записать выражения для А-параметров пассивного четырёхполюсника в функции частоты. Рассчитать эти параметры на заданной частоте f. Проверить принцип взаимности.

1.4 Рассчитать А-параметры усилителя, используя линейную схему замещения с зависимыми источниками.

1.5 Рассчитать А-параметры каскадного соединения пассивного и активного четырёхполюсников.

1.6 Определить входное сопротивление усилителя, нагруженного на резистор , через А-параметры усилителя.

1.7 Найти коэффициент передачи по напряжению пассивного четырёхполюсника, нагруженного на сопротивление .

1.8 Найти коэффициент передачи по напряжению активного четырёхполюсника(усилителя), нагруженного на сопротивление .

1.9 Найти коэффициент передачи по напряжению К каскадного соединения четырёхполюсников двумя способами:

а) по А-параметрам каскадного соединения четырёхполюсников с активной нагрузкой;

б) по коэффициентам передачи и четырёхполюсников.

1.10 Рассчитать комплексную частотную характеристику(КЧХ) по напряжению пассивного четырёхполюсника, нагруженного на сопротивление .

1.11 Рассчитать КЧХ по напряжению каскадного соединения пассивного и активного четырёхполюсников.

1.12 Построить частотные характеристики АЧХ - и ФЧХ - в одной системе координат. Сделать вывод о фильтрующих свойствах и приняв за полосу прозрачности диапазон частот, в котором , где - максимальное значение модуля коэффициента передачи по напряжению цепи.

1.13 Составить схему для расчёта переходного процесса, возникающего при подключении синусоидального ЭДС к R-C цепи (рис.1.2), нагруженной на сопротивление . Переходной процесс рассчитать на частоте . Найти напряжение на резисторе в переходном режиме. Построить на одном графике напряжение входного и выходного сигналов в зависимости от времени.

2 Расчётная часть

Вариант 224531-3

Y₁, Y₂, Z₃

R₀=0 кОм

R₁=0,8 кОм

C₁=0,0 мкФ

R₂=5 кОм

C₂=0,6 мкФ

R₃=10,5 кОм

C₃=0,9 мкФ

R_Н=2,3 кОм

E=250 мВ; ψ_Е=60 град

УСИЛИТЕЛЬ В

2.1 Строим схему пассивного (рис.2.1) и активного (рис.2.2) четырёхполюсников.

2. Записываем выражения для А-параметров пассивного четырёхполюсника в функции частоты :

;

;

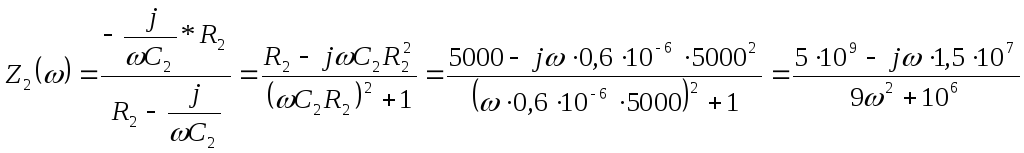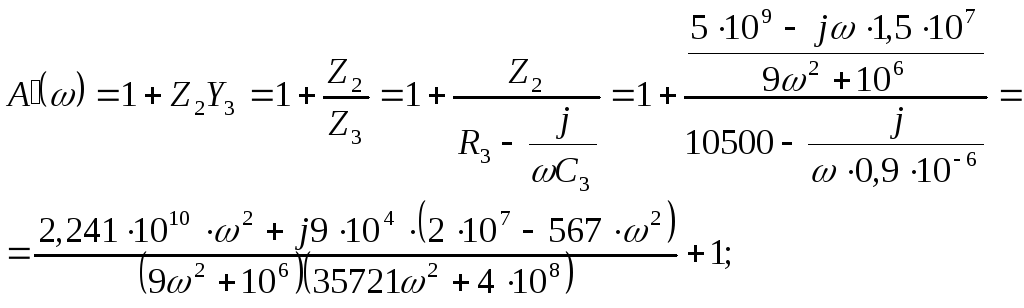
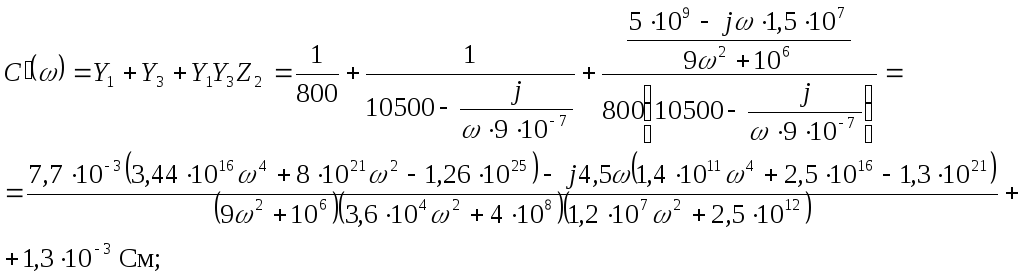
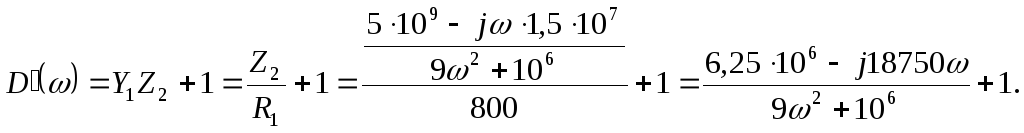
Рассчитываем эти параметры на заданной частоте f=50 Гц, т.е. ω=2πf=

=2∙3,14∙50=314 c^–1:

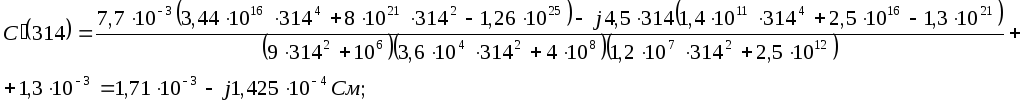
Проверяем принцип взаимности:

2.3 Рассчитываем А-параметры усилителя, используя линейную схему замещения с зависимыми источниками(рис.2.3), учитывая, что

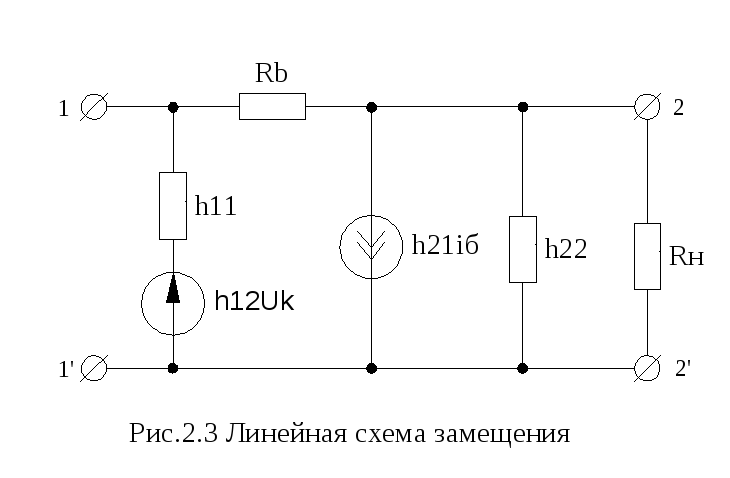
По данной схеме составляем систему уравнений по законам Кирхгофа:

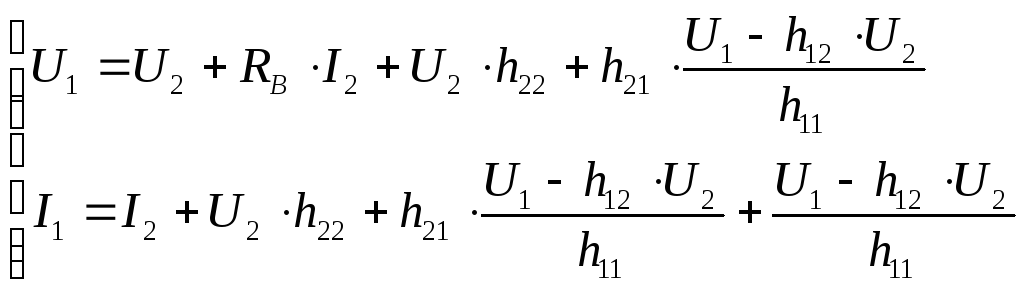
Затем приводим её к следующему виду:

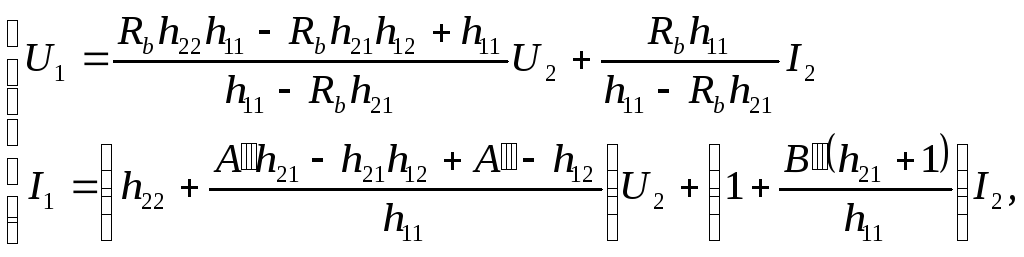
где и — это А и В параметры усилителя соответственно.

Из данной системы уравнений определяем А-параметры активного четырёхполюсника:

;

;

2.4 Рассчитываем А-параметры каскадного соединения пассивного и активного четырёхполюсников (рис.1.1):

Из данной матрицы следует, что А-параметры каскадного соединения пассивного и активного четырёхполюсников равны:

;

;

.

2.5 Определяем входное сопротивление усилителя, нагруженного на резистор , через А-параметры усилителя:

2.6 Определяем коэффициент передачи по напряжению пассивного четырёхполюсника, нагруженного на сопротивление :

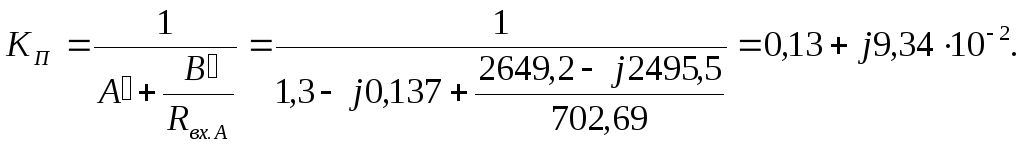
2.7 Определяем коэффициент передачи по напряжению активного четырёхполюсника(усилителя), нагруженного на сопротивление :

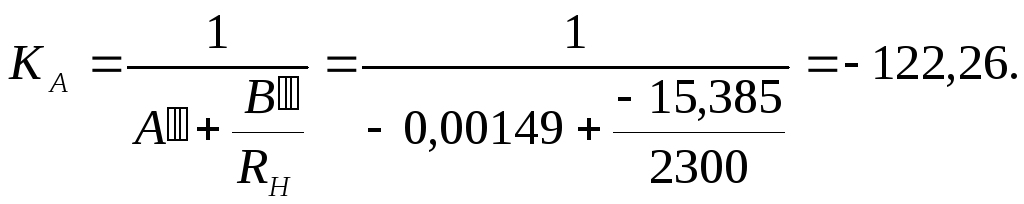
2.8 Определяем коэффициент передачи по напряжению К каскадного соединения четырёхполюсников двумя способами:

а) по А-параметрам каскадного соединения четырёхполюсников с активной нагрузкой:

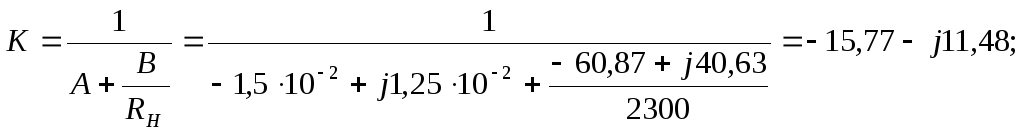
б) по коэффициентам передачи и :

2.9 Рассчитаем комплексную частотную характеристику (КЧХ) по напряжению пассивного четырёхполюсника, нагруженного на сопротивление :

.

Из этого выражения находим модуль и аргумент :

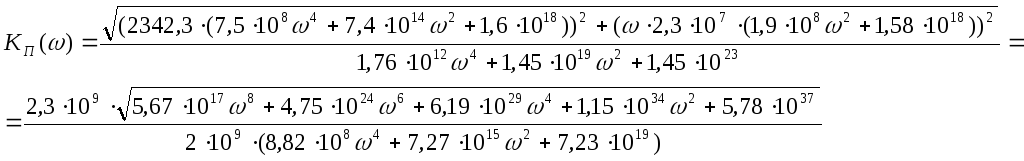
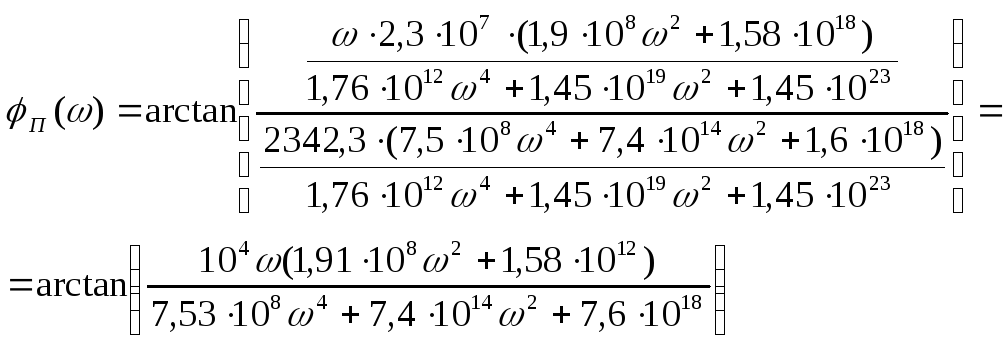
2.10 Рассчитаем комплексную частотную характеристику (КЧХ) по напряжению каскадного соединения пассивного и активного четырёхполюсников:

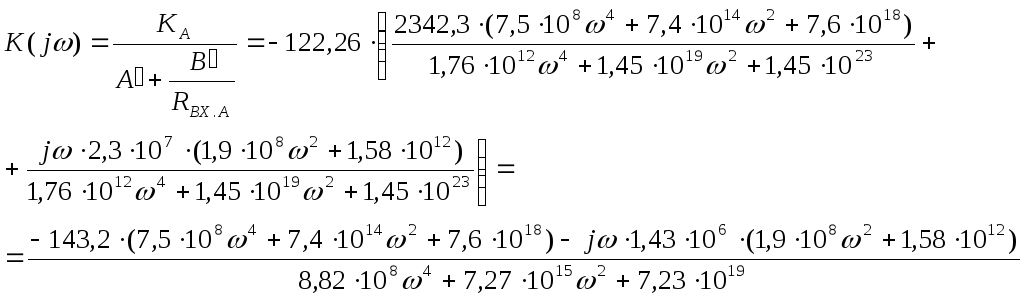
Из этого выражения находим и :

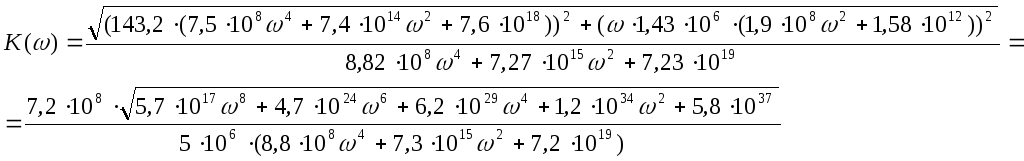
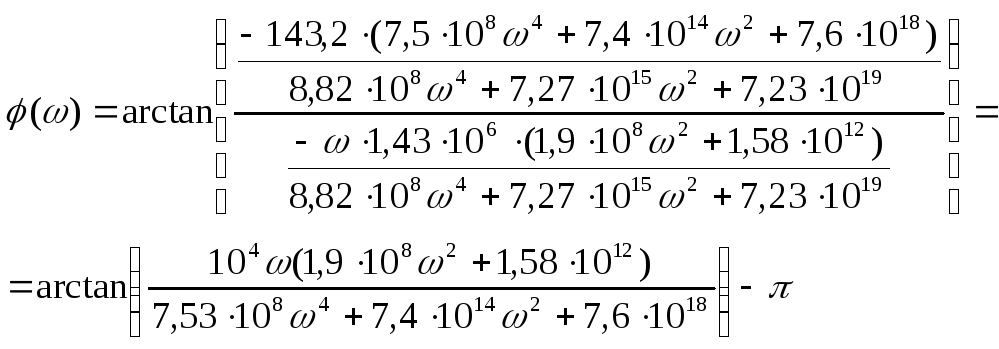
2.11 Построим частотные характеристики АЧХ - и ФЧХ - в одной системе координат (рис.2.4).

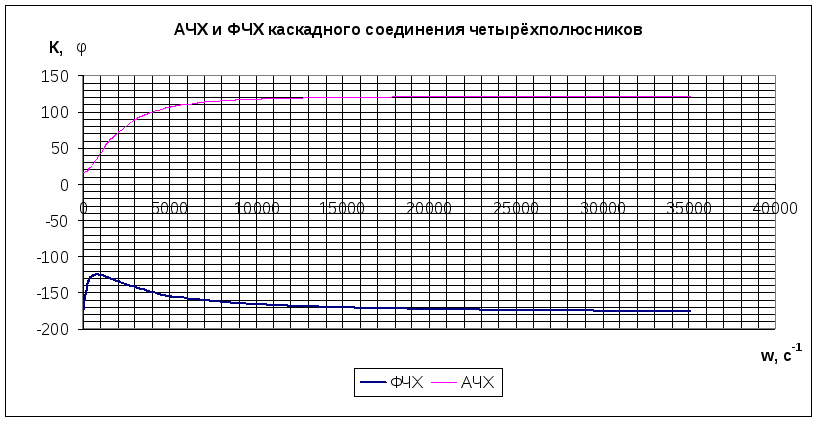
Рис.2.4 График зависимости и

Найдём : . Приняв за полосу прозрачности диапазон частот, в котором , т.е. К>86,45, то можно сказать, что каскадное соединение четырёхполюсников имеет высокочастотные фильтрующие свойства.

2.12 Переходный процесс, возникающий при подключении каскадного соединения пассивного четырёхполюсника и усилителя к синусоидальному источнику напряжения с частотой f=50 Гц, рассчитываем по схеме представленной на рисунке 2.5.

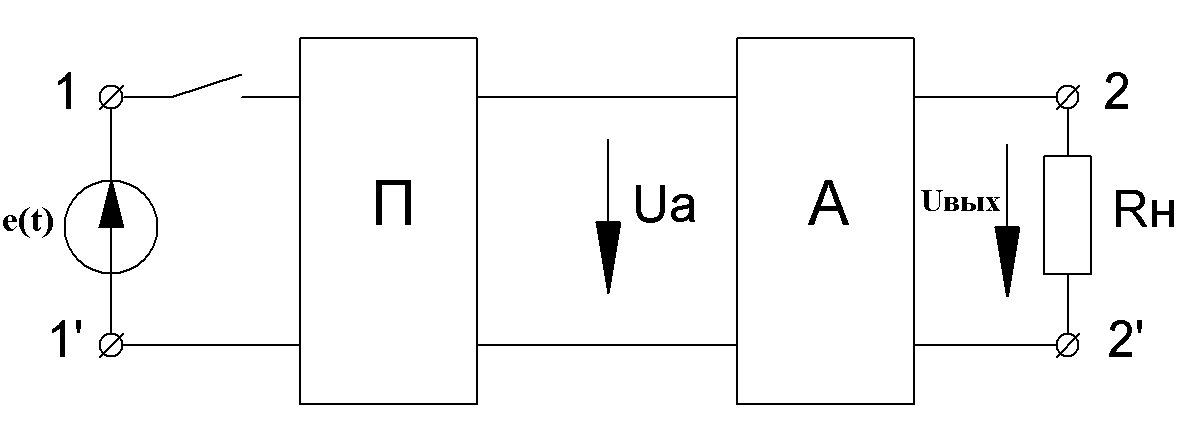
Рис.2.5 Схема для расчета переходного процесса

После коммутации получается двухконтурная цепь второго порядка с нулевыми независимыми начальными условиями для напряжения на ёмкости. Поскольку коэффициент передачи усилителя К_а не зависит от частоты, необходимо заменить усилитель с нагрузкой R_Н входным сопротивлением усилителя . Тогда схема примет вид представленный на рисунке 2.6.

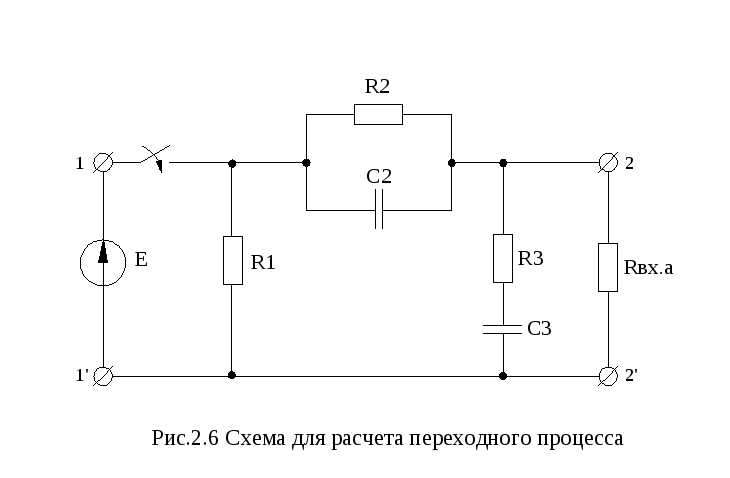
Входное напряжение усилителя имеет вид:

Рассчитаем напряжение на операторным методом. Составляем операторную схему замещения в послекоммутационном режиме (рис.2.7).

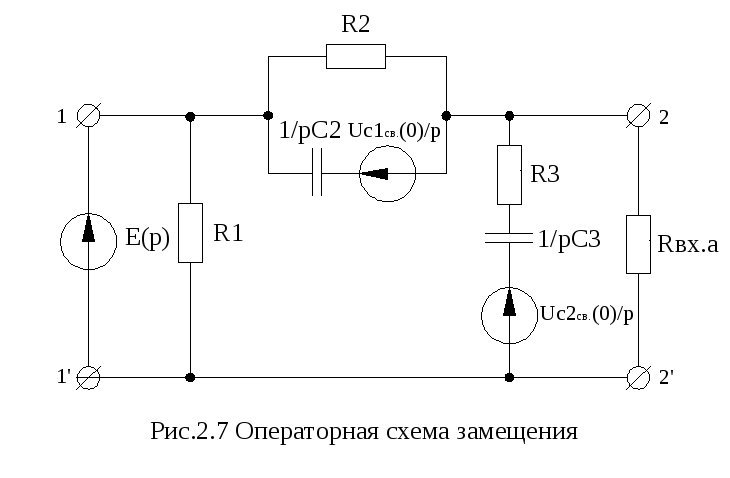
Начальные условия для свободных составляющих:

Рассчитаем по методу контурных токов (рис.2.8) значение тока на сопротивлении .

Преобразуем значение ЭДС в операторный вид:

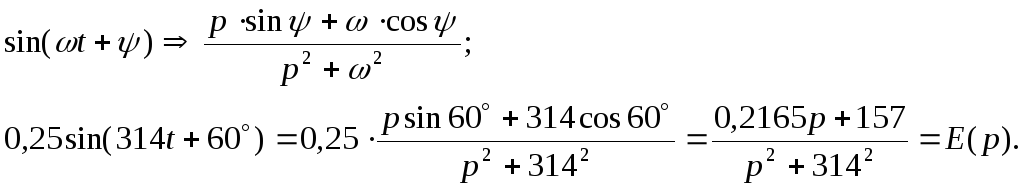
По методу контурных токов составим систему уравнений:

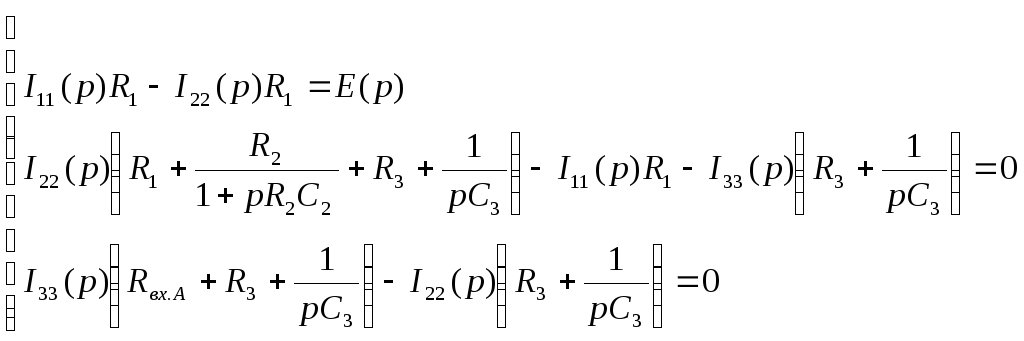
Решив данную систему, получаем ток через сопротивление :

Напряжение на входе усилителя:

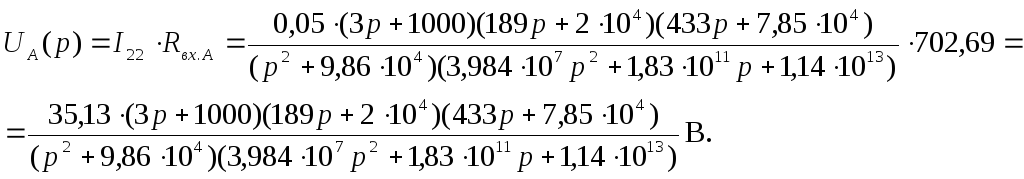
Применяем теорему разложения:

Найдём корни характеристического уравнения вида:

; ; .

Подставив в числитель, полученного напряжения на входе усилителя, значения корней характеристического уравнения получим:

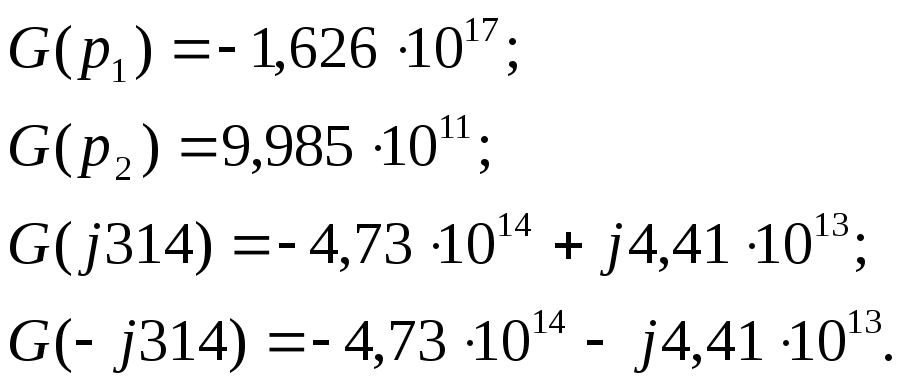
Продифференцируем знаменатель полученного напряжения на входе усилителя:

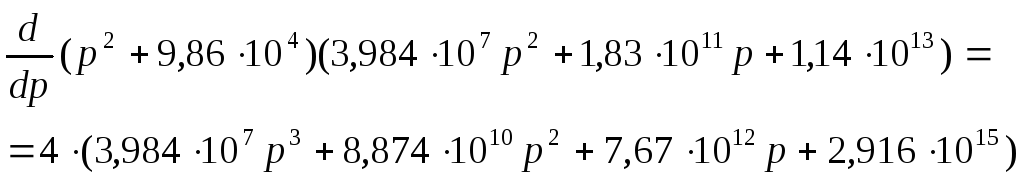
Подставив в полученное выражение значения корней характеристического уравнения, получим:

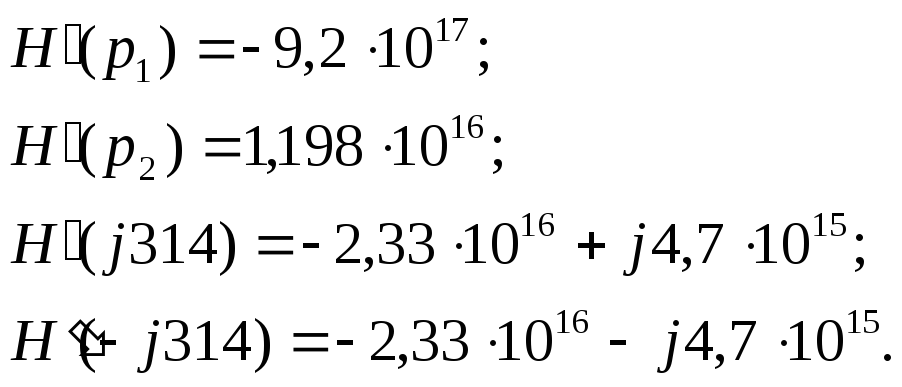
Определим значение напряжения на входе усилителя:

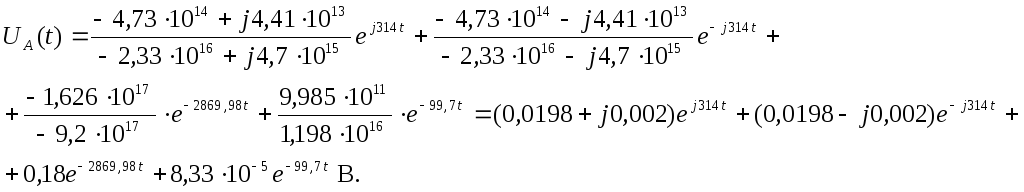Упростим отдельно выражение для вынужденной составляющей напряжения, применяя формулу Эйлера:

Затем применим формулу

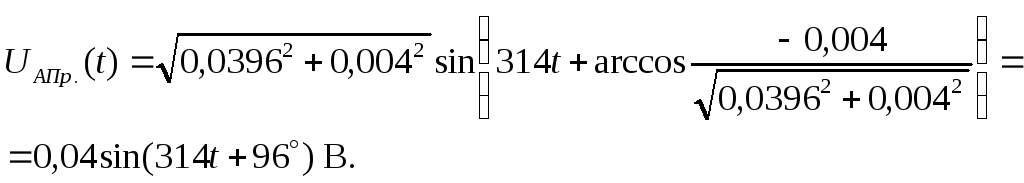
Определяем напряжение на выходе усилителя:

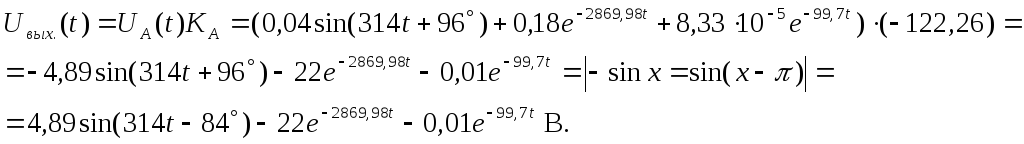
Построим графики напряжения входного и выходного сигналов в зависимости от времени (рис.2.9).

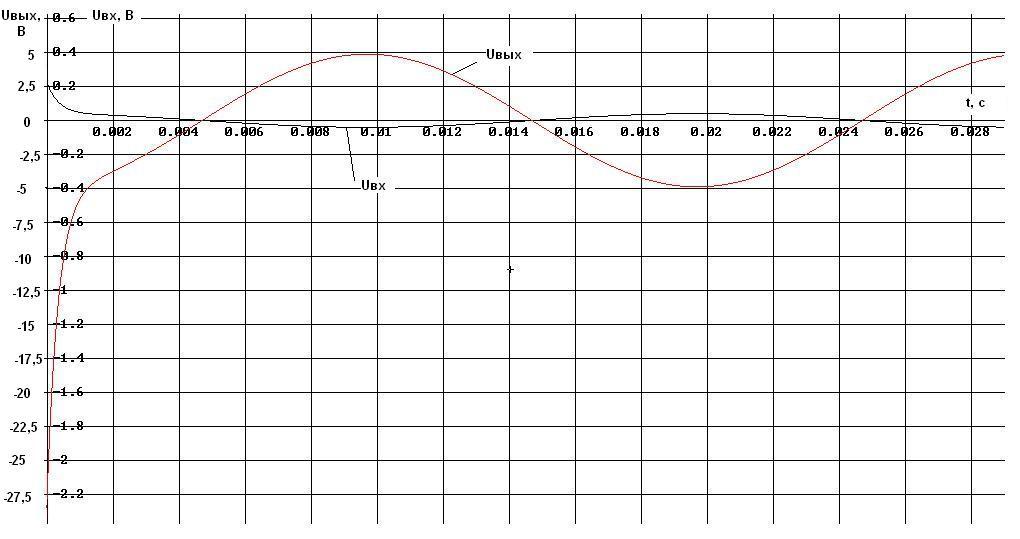
Рис.2.9 Зависимость входного и выходного напряжения от времени

3 Список использованной литературы:

1. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 2.— 4-е изд. / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин.— СПб.: Питер, 2003. — 463 с.: ил.

2. Задачник по теоретическим основам электротехники (теория цепей). Учеб. пособие для вузов. Под общ. ред. проф. К. М. Поливанова. Изд. 3-е, перераб. и доп. М., «Энергия», 1973.

3. Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич. спец. вузов.— 4-е изд., перераб. и доп.— М.: Высш. шк., 1990.— 544 с.: ил.