8. Z – преобразование

Z - преобразование импульсной характеристики

цепи записывается в виде:

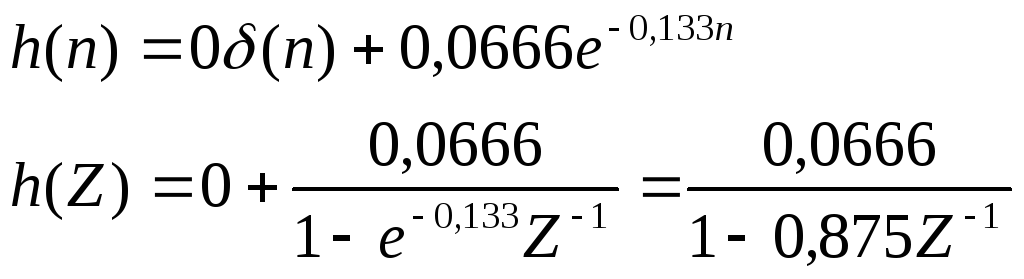
Учитывая, что Z-преобразование входного и выходного дискретных сигналов связаны между собой соотношением Y(Z)=X(Z)*H(Z), можем записать:

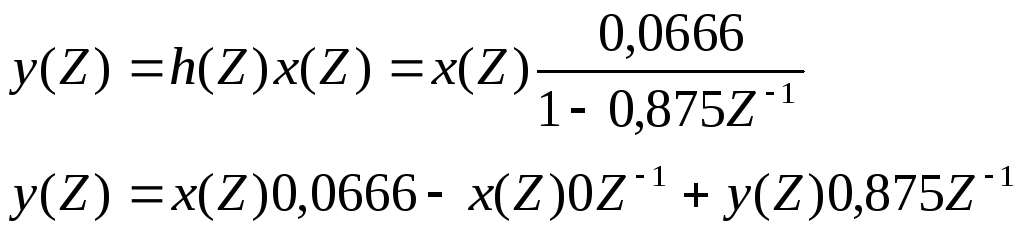
a₀ = 0,0666; a₁ = 0; b₁ = 0,875

Рисунок 8.1 - Схема дискретной цепи

Рисунок 8.2 - Схема дискретной цепи в конаническом виде

9. Дискретный корректор.

Компенсация искажений сигнала, вносимых заданной цепью может быть выполнена с помощью корректора, подключаемого к входу или выходу цепи. Проблема коррекции искажений решается при обработке дискретизированного сигнала. В этом случае Z - преобразование передаточной функции корректора H’(Z) находится как величина, обратная H(Z) исходной цепи.

Отсчеты импульсной характеристики дискретного корректора находятся делением полинома числителя на полином знаменателя.

Для примера определим первые 10 отсчетов импульсной характеристики корректора и восстановим первые 10 значений сигнала на входе дискретной цепи.

Z^-1

Z^-1

a’₀=15,015; a’₁=-13,138; b’₁=0

Рисунок 9.1 - Схема дискретной цепи корректора.

Рисунок 9.2 - Схема дискретного корректора в конаническом виде

Дискретные значения сигнала на выходе корректора вычисляются с помощью формулы дискретной свертки.

Таблица 9.1 - Дискретные значения импульсной характеристики корректора и сигнала на его выходе.

t,мс	0	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8
n	0	1	2	3	4	5	6	7	8	9
U2,В	0,666	1,249	1,579	2,209	2,599	2,939	3,239	3,499	3,729	3,929
h’(n)	15,015	-13,138	0	0	0	0	0	0	0	0
U2,В	10	10,0038	10,002	10,058	10,002	9,988	10,021	9,984	10,021	10,002

Полученные результаты практически совпадают со значениями дискретных отсчетов входного сигнала U₁(n), приведенными в таблице 3.

10. Ачх дискретной цепи и дискретного корректора

Рассчитаем АЧХ дискретной цепи и корректора:

Для получения частотных характеристик, необходимозаменитьZ^-1→ → e^jωT

f = 0:

f = 1,25 кГц:

f = 2,5 кГц:

f = 3,75 кГц:

f = 5 кГц:

f = 0:

f = 1,25 кГц:

f = 2,5 кГц:

f = 3,75 кГц:

f = 5 кГц:

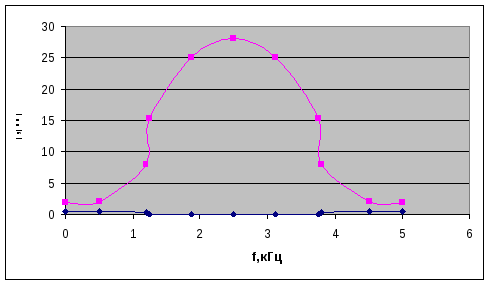
Рис 10.1 АЧХ дискретной цепи и корректора.

Заключение

В данной курсовой работе я закрепил знания, полученные при изучении классического, операторного и спектрального методов расчета процессов в линейных электрических цепях, а также теоретических основ анализа дискретных сигналов и линейных дискретных систем.

Список литературы

1. Бакалов В.П. Игнатов А.Н. Крук Б.И. «Основы теории электрических цепей и электроники». М.: Радио и связь,1989

2. Зевеке Г.В. Ионкин П.А. Нетушил А.В. Страхов С.В. «Основы теории цепей».М.: Энергоатомиздат, 1989

3. Баскаков М.Р. Каблукова М.В. «Радиотехнические цепи и сигналы».М.: Высшая школа, 1988

4. Белецкий А.Ф. Теория линейных электрических цепей: Учебник для вузов. – М.: Радио и связь, 1986

5. Методические указания к курсовой работе

6. Конспект лекций по курсу ТЭЦ