Контрольная работа1
.doc1.1. Определить наиболее рациональный метод расчета схемы.

Метод узловых потенциалов.
![]() тогда
потенциал узла a
равен:
тогда
потенциал узла a
равен:
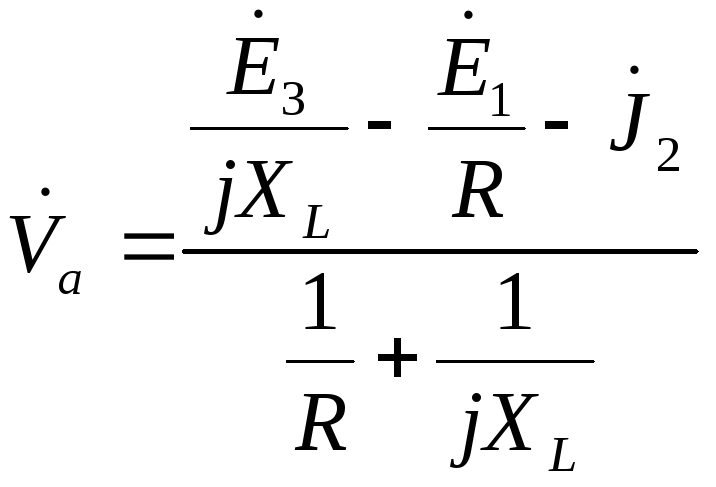
Токи в ветвях:
![]() и
и
![]() .
.
Метод контурных токов.
![]()
![]()
![]()
1.2. Составить схему МЗК для расчета токов в ветвях.
![]()
Расчет в MathCAD с подстановкой численных значений.

2.1. Из каких элементов состоит сопротивление
![]() ?
?
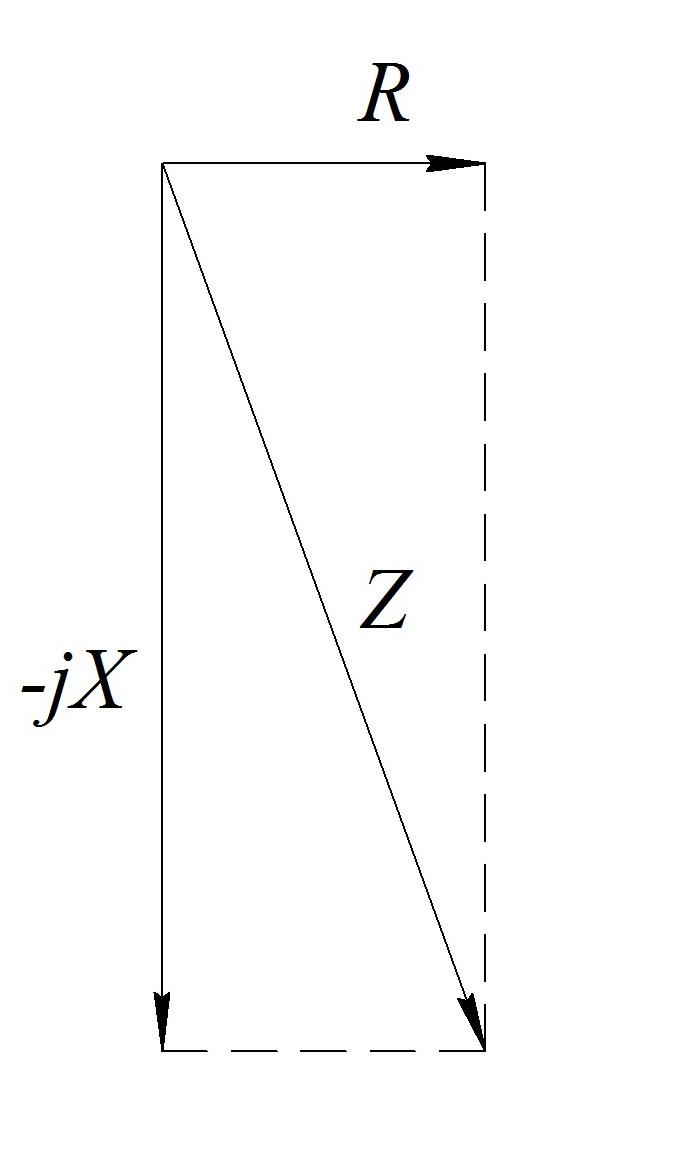
Разложим вектор Z на комплексные составляющие:
![]()
![]()
Действительная часть
![]() соответствует активной составляющей
сопротивления.
соответствует активной составляющей
сопротивления.
Мнимая часть
![]() соответствует реактивной составляющей
сопротивления.
соответствует реактивной составляющей
сопротивления.
2.2. Построить вектор
![]() ,
если известен вектор
,
если известен вектор
![]() .
.
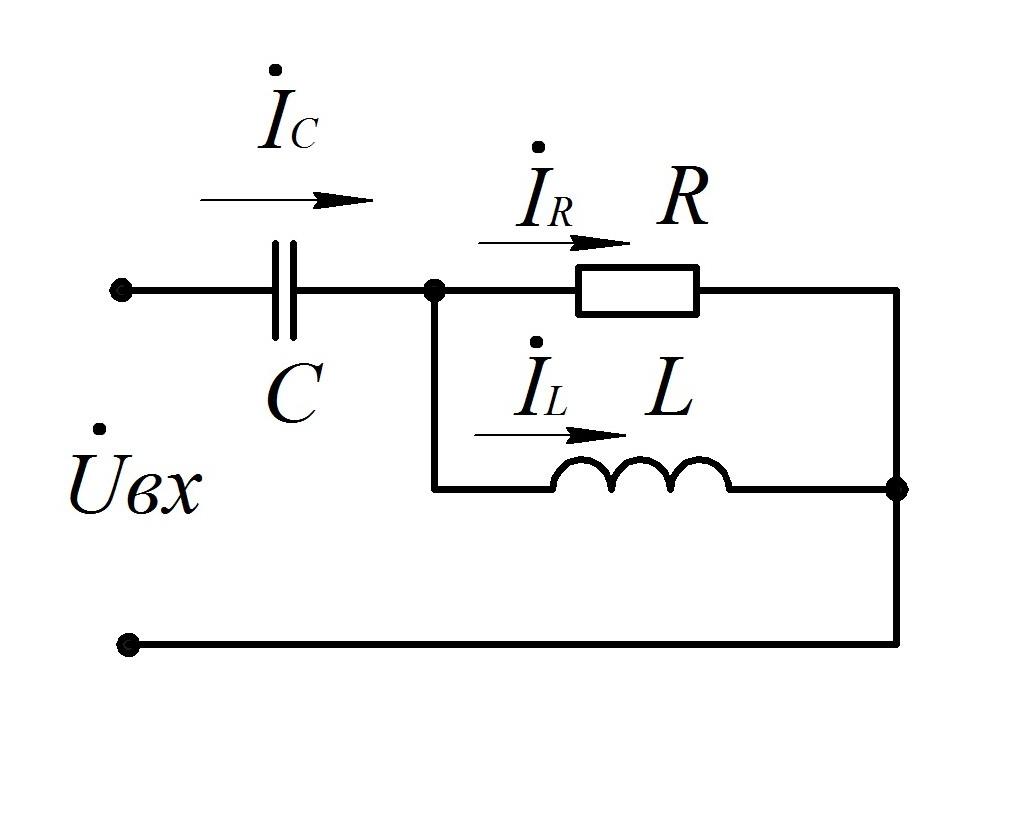
Решение:
Построения проводим в следующей последовательности (номера соответствуют номерам на рисунке):
-
Откладываем на комплексной плоскости вектор тока
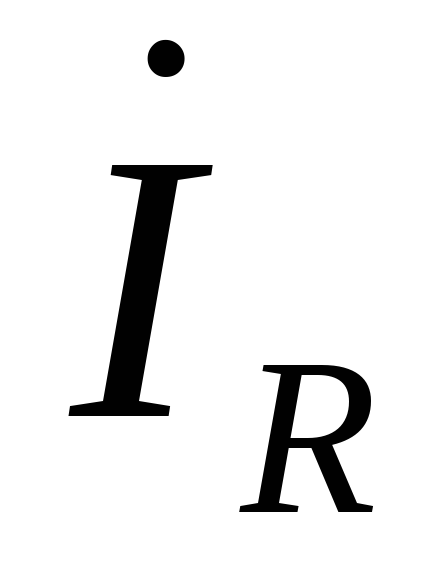 .
. -
Так как вектор падения напряжения на резисторе совпадает с направлением тока на нем, то откладываем вектор
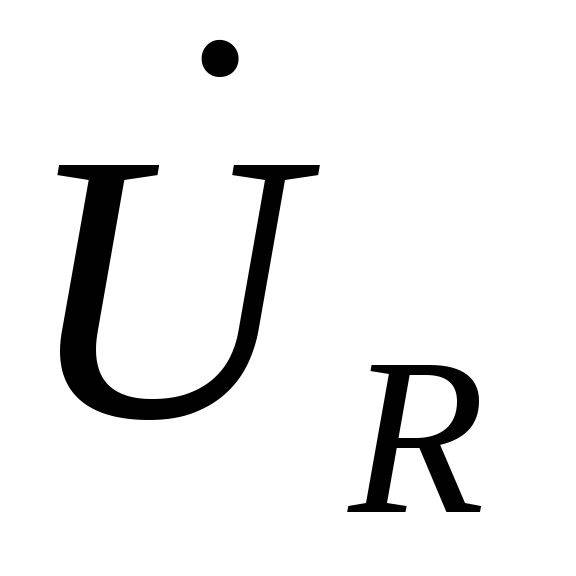 .
Так как сопротивление R
и индуктивность L
соединены параллельно, то вектор
.
Так как сопротивление R
и индуктивность L
соединены параллельно, то вектор
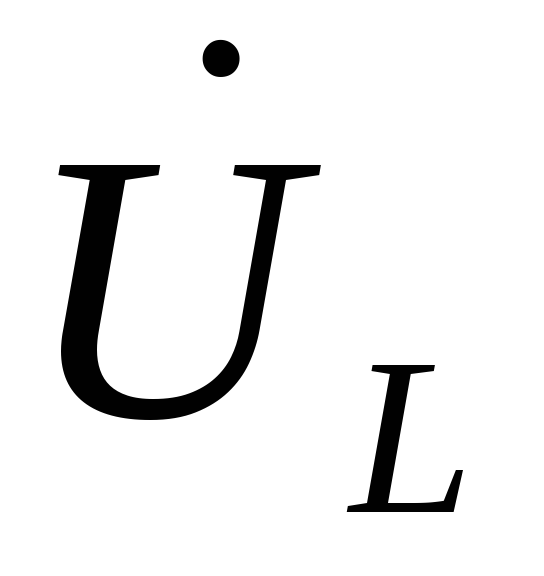 будет совпадать с вектором
будет совпадать с вектором
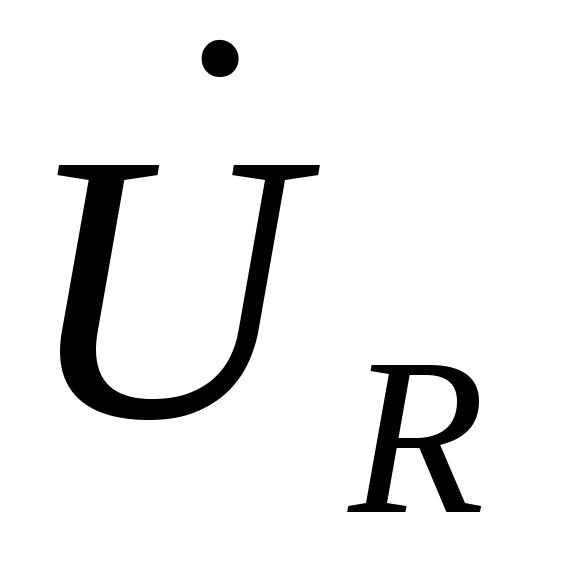 .
. -
Напряжение на индуктивности опережает ток на 90° и соответствующим образом откладываем вектор тока
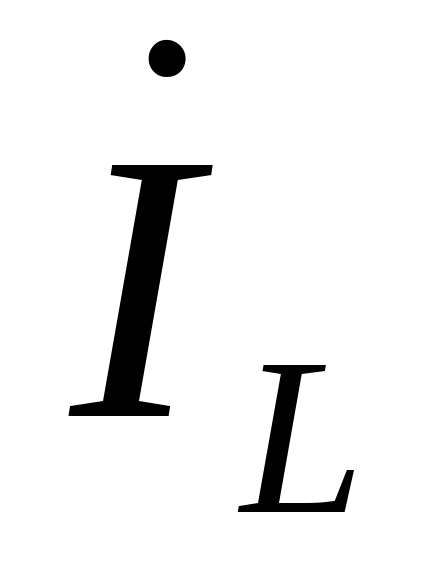 ,
протекающий в индуктивности. (-90° между
,
протекающий в индуктивности. (-90° между
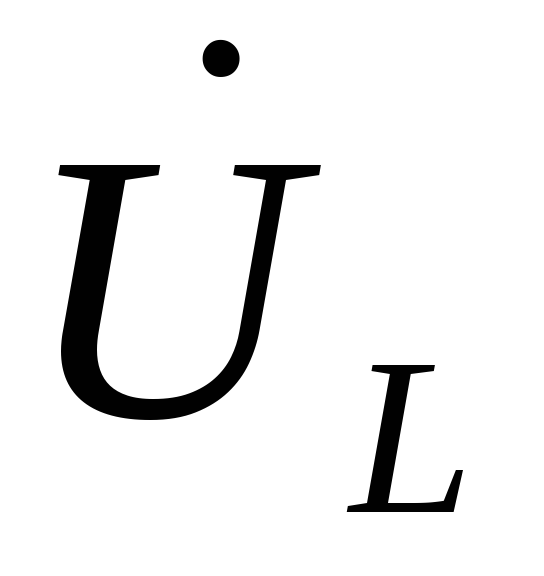 и
и
 )
) -
Определяем ток
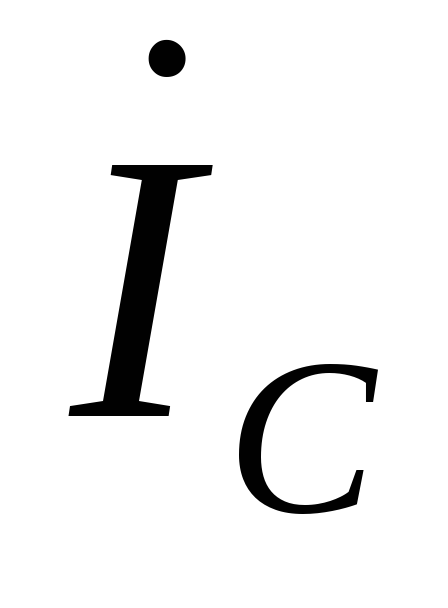 ,
который по первому закону Кирхгофа
равен сумме токов
,
который по первому закону Кирхгофа
равен сумме токов
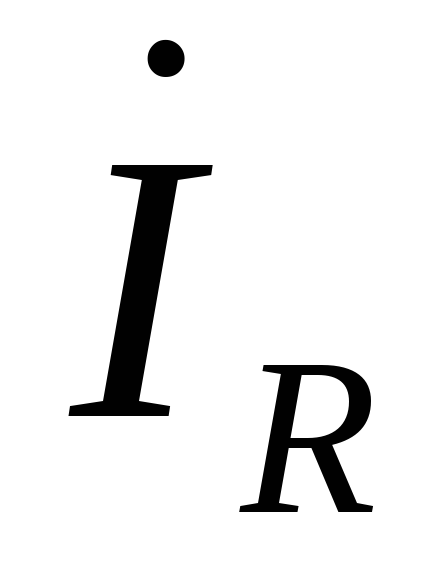 и
и
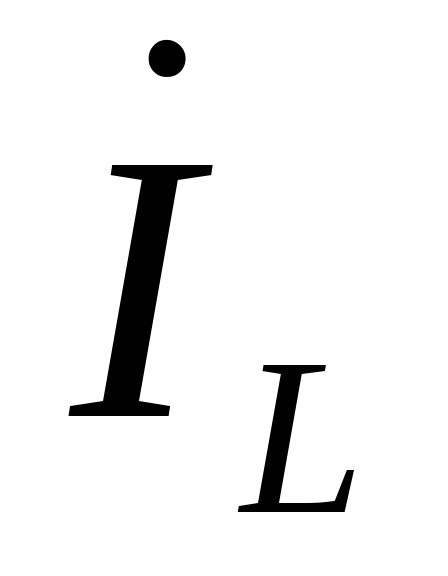 .
. -
Напряжение на емкости отстает от тока на 90° и соответствующим образом откладываем вектор напряжения
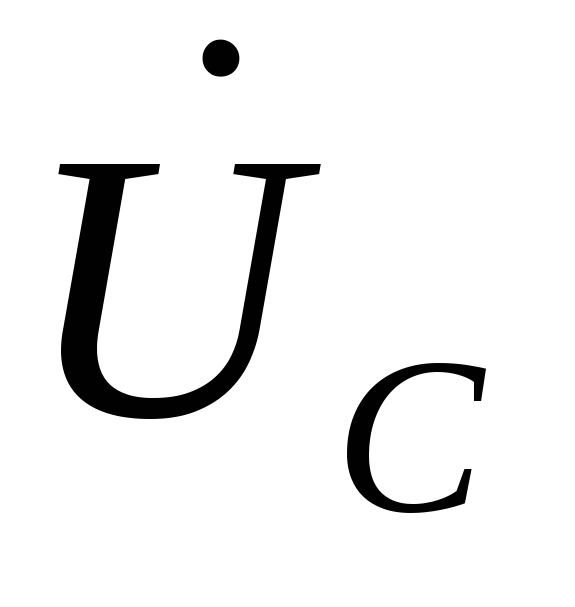 ,
падающей на емкости. (90° между
,
падающей на емкости. (90° между
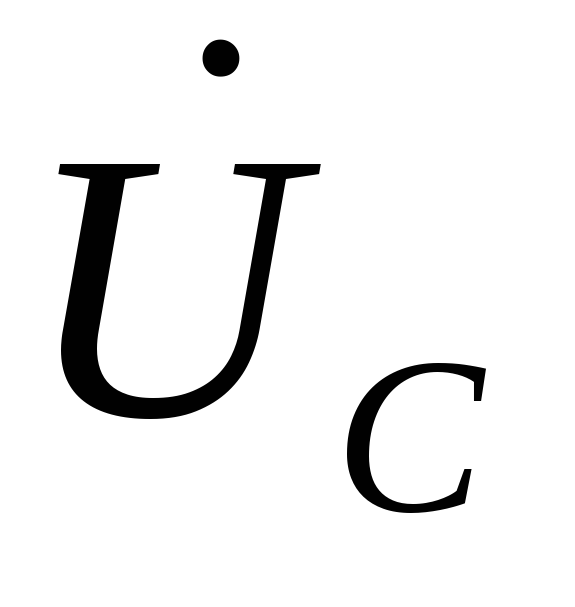 и
и
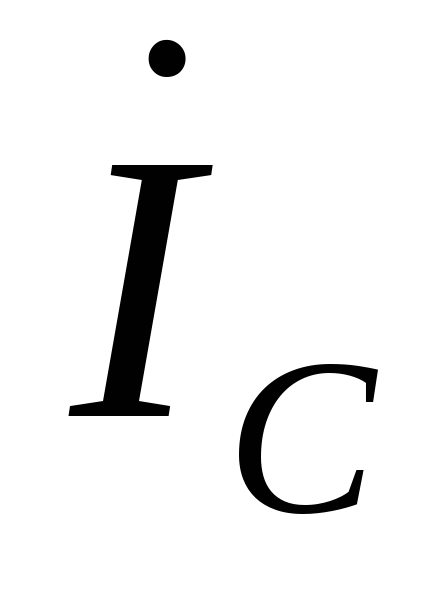 )
) -
Определяем вектор входного напряжения
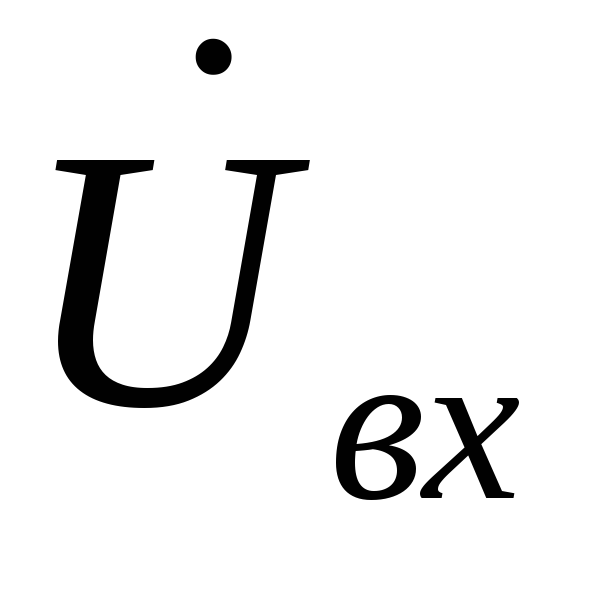 ,
который по второму закона Кирхгофа
равен сумме падений напряжений
,
который по второму закона Кирхгофа
равен сумме падений напряжений
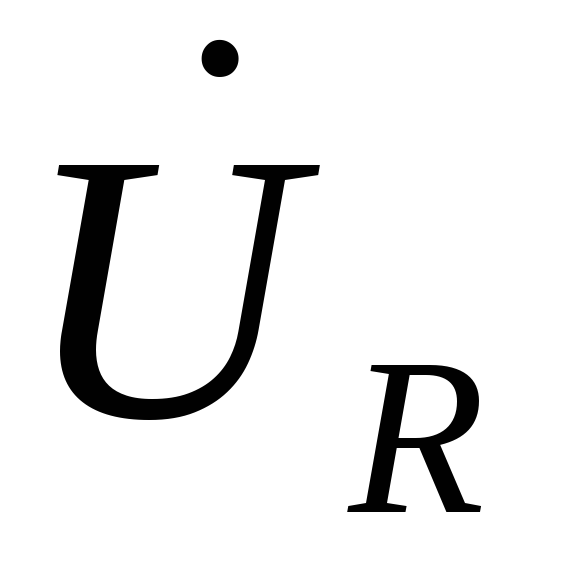 и
и
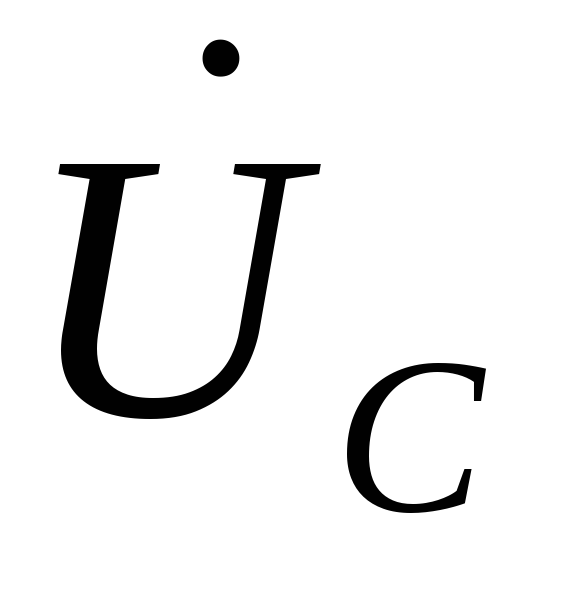 .
.

3.1. Расчет переходного процесса классическим методом.
|
|
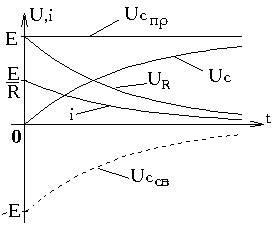
Если RC -цепь, изображенная на рисунке, в момент времени t=0 подключается к источнику внешнего напряжения, то для неё при t >= 0 справедливо уравнение UC+UR=e(t),
UC=UCпр+UCсв=UCпр+Aept, где Р - корень характеристического уравнения RCP+1=0, P=-1/RC; A -постоянная интегрирования; UCпр –определяется видом подключаемого источника и величинами R, С.
|
При подключении RC -цепи к источнику постоянного напряжения величина принуждённой составляющей должна быть равна внешнему напряжению Е, так как при t ёмкость заряжается до напряжения источника питания.
Следовательно, UC=E+Aept.
Если запаса энергии в цепи до подключения внешнего источника не было,
|
|
то UC (0)=UC (0-)=0=UСпр+UСсв(0), 0=Е+А,
А=-Е, UC(t)=E(1-e-t/RC),
ток
в цепи
UR=Ri=Ee-t/c, где C=RC -постоянная времени, характеризующая скорость изменения свободных составляющих тока и напряжений на элементах. |
3.2. Расчет переходного процесса операторным методом.
Составим операторную схему замещения цепи.
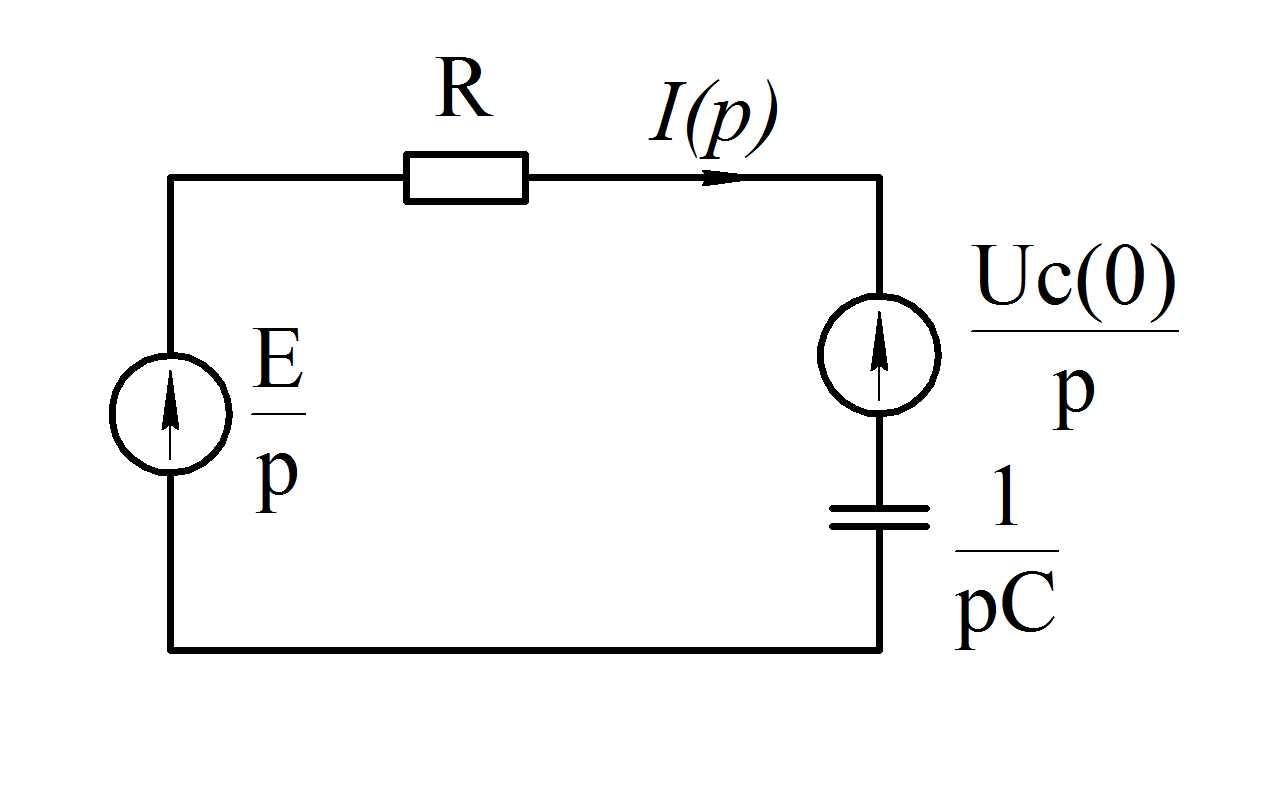
Запишем уравнение для тока, протекающего в цепи.
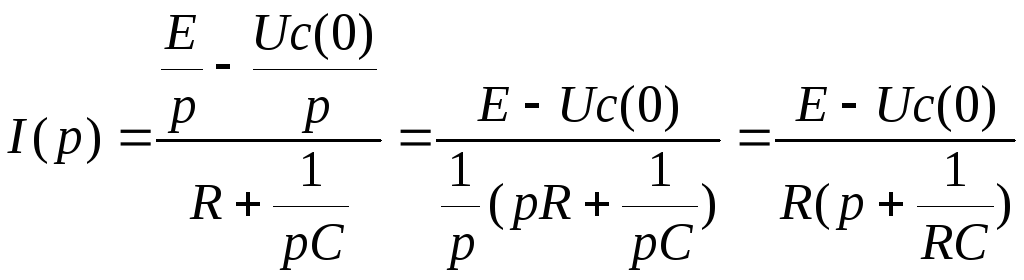
Напряжение на резисторе:
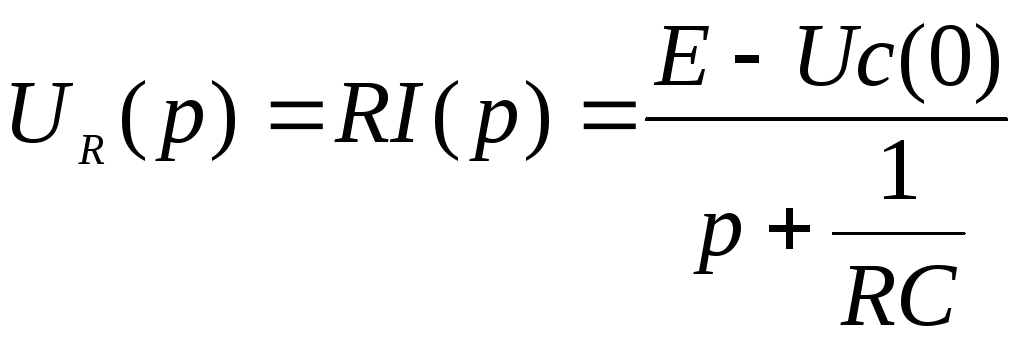 .
.
Переходя к оригиналам получаем:
![]() .
.
Так как конденсатор в начальный момент времени не заряжен (Uc(0)=0), то получаем выражение:
![]() .
.