Примеры расчётов переходных процессов в цепях первого порядка.

Пример 1. Включение дросселя на постоянное напряжение.

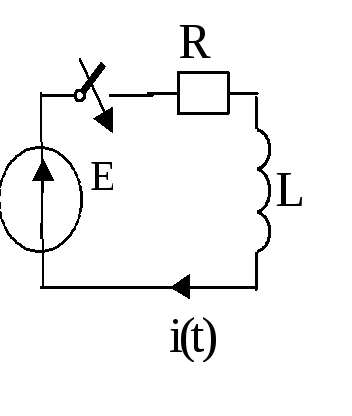
Рис. 1.4.

1. Записываем решение как сумму свободной и установившейся составляющих

.

2. Находим установившуюся составляющую

.

3. Находим свободную составляющую.

   1. Методом входного операторного сопротивления составляем характеристическое уравнение цепи после коммутации.

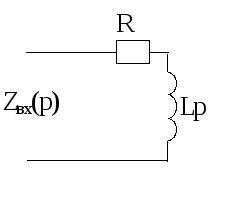
      Из Zвх(p)=0 получаем характеристическое уравнение R+Lp=0 p=-R/L, с-1

   2. По виду корня характеристического уравнения определяем общий вид свободной составляющей

3. Определяем постоянную интегрирования. Из цепи до коммутации получим ННУ i(0_-)=0, A. По первому закону коммутации получим ток в индуктивности в t=0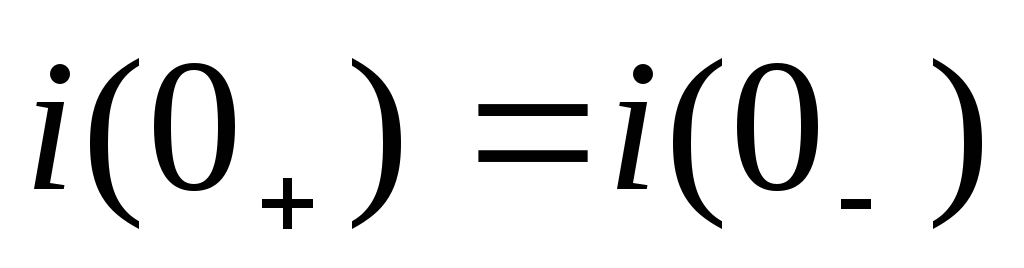₊ . Тогда после подстановки в уравнение п. 1, получим

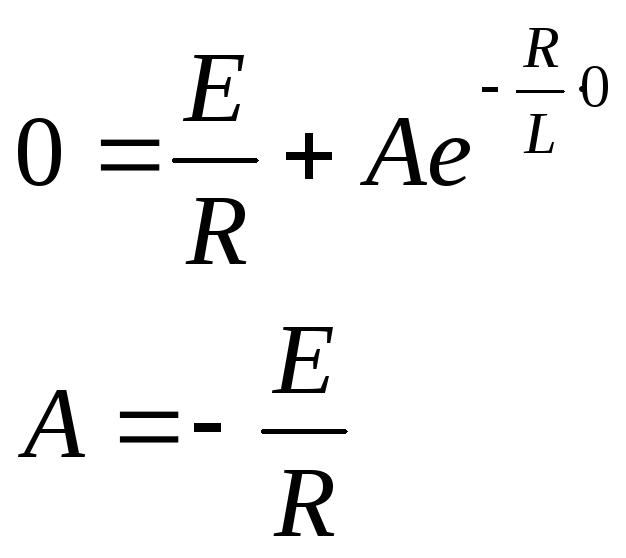
Ответ: , где . При записи ответа используют величину постоянной времени переходного процесса, которая имеет размерность времени и характеризует скорость затухания свободной составляющей. Здесь  равна времени в течении которого величина уменьшается в е=2.71… раз. На практике принято ожидать время окончания переходного процесса в пределах (3-5). Строим график тока:

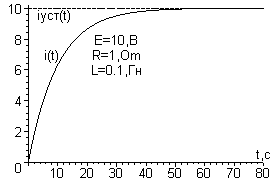
Рис.1.5.

Пример 2. Включение дросселя на синусоидальное напряжение.

-фаза коммутации Рис. 1.6.

1. Записываем решение как сумму свободной и установившейся составляющих . 2. Установившийся ток находим комплексным методом.

3. Находим свободную составляющую.

3.1. Определение общего вида свободной составляющей смотри в примере 1.

3.2. Определяем постоянную интегрирования.

По первому закону коммутации имеем ток в цепи при t=0₊ равным 0. Тогда

,

.

4. Записываем ответ и строим график:

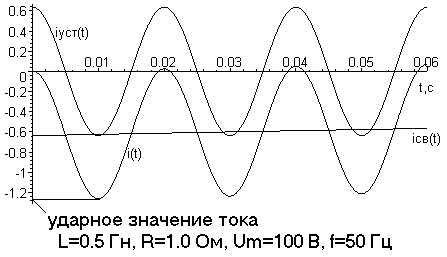
Рис. 1.7.

Здесь следует заметить, что интенсивность переходного процесса зависит ещё и от фазы коммутации. Для параметров, приведённых на графике имеет место близость к максимально возможному переходному процессу при фазе коммутации 180^о. При слабом затухании с увеличением постоянной времени () угол сопротивления90^о, тогда при 180^о будет иметь место максимальная интенсивность переходного процесса и ток дросселя может достигать ударного значения, равного удвоенной амплитуде установившейся величины.

Пример 3. Разряд конденсатора на резистор.

1. Записываем решение как сумму свободной и установившейся составляющих

.

2. Находим установившуюся составляющую

.

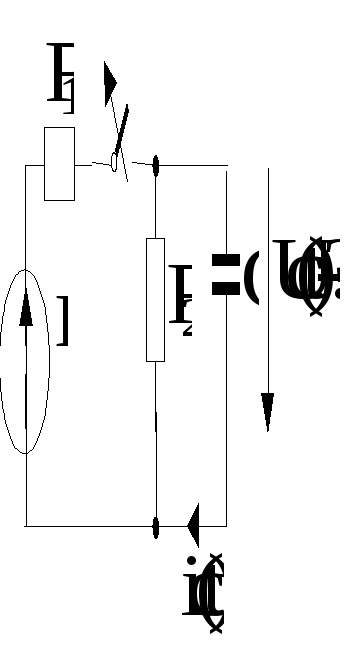
Рис. 1.8.

3. Находим свободную составляющую.

   1. Методом входного операторного сопротивления составляем характеристическое уравнение цепи после коммутации

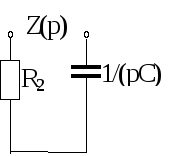
      Рис. 1.9.

      Zвх(p)=0 – характеристическое уравнение R+1/(pC)=0 p=-1/(RC), с-1

   2. По виду корня характеристического уравнения определяем общий вид свободной составляющей

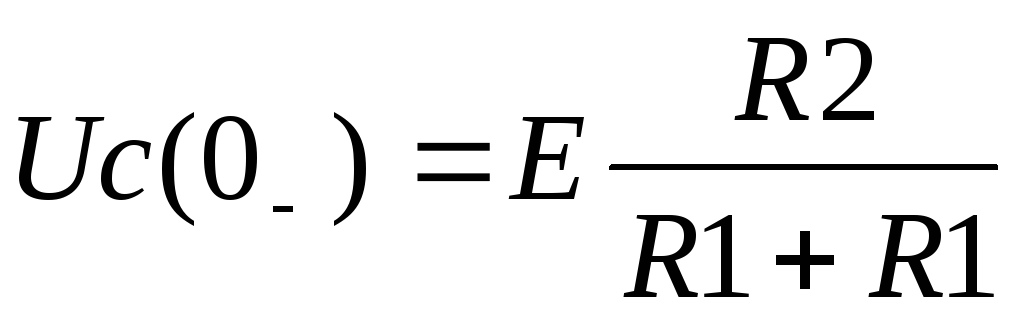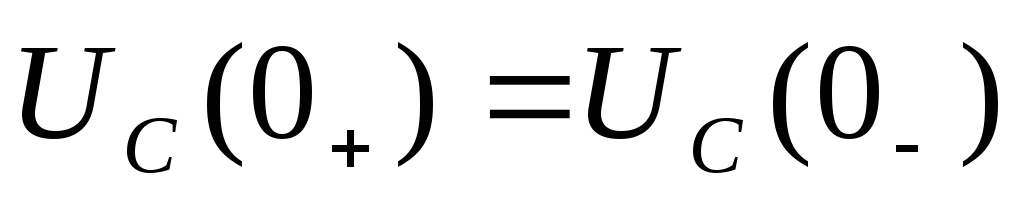3. Определяем постоянную интегрирования. Из цепи до коммутации получим ННУ , В. По второму закону коммутации получим напряжение на ёмкости вt=0₊. Тогда уравение п.1 для t=0₊ примет вид

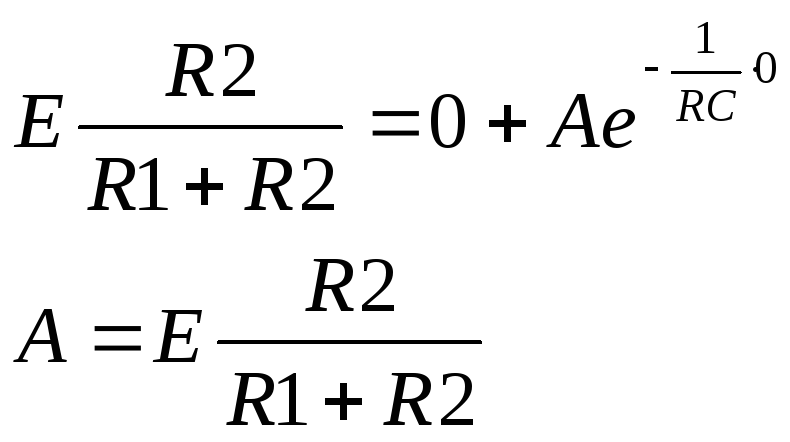
Ответ: , где . Строим график напряжения и тока в ёмкости:

Рис. 1.10.