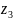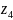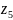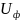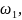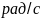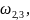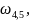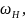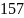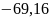- •Факультет інженерної механіки
- •1 Структурный и кинематический анализ рычажного механизма
- •Структурный анализ рычажногомеханизма
- •1.2 Построение планов механизма, скоростей и ускорений
- •2 Силовое исследование рычажного механизма
- •2.1 Определение масс звеньев, сил тяжести, и центральных моментов инерции
- •2.2 Определение сил реакций в кинематических парах и уравновешивающего момента методом академика Бруевича
- •3 Синтез зубчатого редуктора
- •3.1 Расчет геометрических параметров зубчатой передачи 1 – 2
- •3.2 Проверка качества зубьев и качества зацепления
- •3.3 Вычисление контрольных размеров
- •3.4 Построение эвольвентного зацепления
- •3.5 Подбор чисел зубьев колес планетарной передачи
- •3.6 Кинематическое исследование зубчатого редуктора двумя методами
- •4 Проектирование кулачкового механизма
- •4.1 Определение законов движения толкателя и построение их графиков
- •4.2 Построение профилей кулачка
3.5 Подбор чисел зубьев колес планетарной передачи
Подбор чисел зубьев
колес
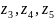 и
и
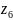 планетарного механизма производится
на ПК в программе ТММ.ЕХЕ.
планетарного механизма производится
на ПК в программе ТММ.ЕХЕ.
Определим исходные данные, необходимые для подбора чисел зубьев.
Угловая скорость первого колеса редуктора:
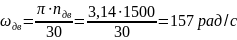
Угловая скорость 2-го и 3-го колеса:
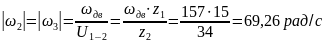
Теоретическое передаточное число:
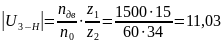
Допустимое
отклонение передаточного числа
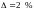 .
.
Полученные варианты чисел зубьев колес представлены в таблице 3.4.
В результате
вычислений получаем для заданного по
условию механизма вариант, обеспечивающий
наименьшие размеры колес:
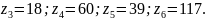
Таблица 3.4 – Результаты подбора чисел зубьев колёс планетарного редуктора
№ |
|
|
|
|
K |
|
|
1 |
18 |
60 |
39 |
117 |
2,3 |
11 |
|
2 |
19 |
63 |
41 |
123 |
2,4 |
10,947 |
|
3 |
20 |
66 |
43 |
129 |
2 |
10,900 |
|
4 |
24 |
80 |
52 |
156 |
2,3,4 |
11 |
|
5 |
25 |
83 |
54 |
162 |
2 |
10,960 |
|
6 |
26 |
86 |
56 |
168 |
2,4 |
10,923 |
|
Выбран вариант №1, т.к для него количество сателлитов К=3 и он обеспечивает наименьшие габариты.
3.6 Кинематическое исследование зубчатого редуктора двумя методами
Определим радиусы начальных окружностей:
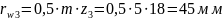
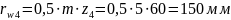
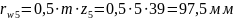
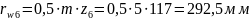
Выбираем масштабный
коэффициент:
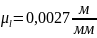 .
С учетом масштабного коэффициента
построим кинематическую схему редуктора.
На кинематической схеме условно
изображаем один сателлит.
.
С учетом масштабного коэффициента
построим кинематическую схему редуктора.
На кинематической схеме условно
изображаем один сателлит.
Вычислим скорость точки А, принадлежащей начальной окружности колеса 1:
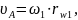
где
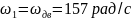
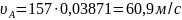
Выбираем
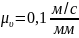 .
.
Скорость точки
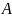 является касательной к начальной
окружности колеса 1
является касательной к начальной
окружности колеса 1
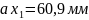 – вектор изображающий скорость точки
. Отрезок
– вектор изображающий скорость точки
. Отрезок
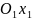 – линия распределения скоростей точек
колеса 1. Из точки
– линия распределения скоростей точек
колеса 1. Из точки
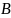 проводим горизонтальную линию. Из точки
через точку
проводим горизонтальную линию. Из точки
через точку
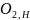 проводим отрезок до пересечения с
горизонтальной линией, проходящей через
точку B.
Полученный отрезок – линия распределения
скоростей точек колес 2 и 3. Отрезок
проводим отрезок до пересечения с
горизонтальной линией, проходящей через
точку B.
Полученный отрезок – линия распределения
скоростей точек колес 2 и 3. Отрезок
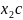 – линия распределения скоростей
сателлита 4. Отрезок
– линия распределения скоростей
сателлита 4. Отрезок
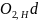 – линия распределения скоростей водила
Н.
– линия распределения скоростей водила
Н.
Строим диаграмму угловых скоростей:
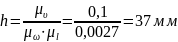
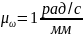
Переношу на диаграмму угловых скоростей точку и распределения линейных скоростей параллельно самим себе.
Получаем угловые скорости колес графическим методом:
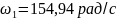
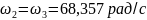
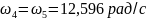
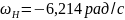
Проверим значения угловых скоростей аналитическим методом – методом Виллиса.
Механизм состоит из последовательно соединенных двух механизмов – простого и планетарного (см. рисунок 2).
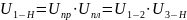
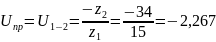
По методу Виллиса
всем звеньям планетарного механизма
дополнительно сообщаем скорость равную
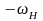 .
При
этом водила остановиться и планетарный
механизм превращается в простой. Получаем
обращенный механизм.
.
При
этом водила остановиться и планетарный
механизм превращается в простой. Получаем
обращенный механизм.
Угловые скорости звеньев в обращенном механизме:
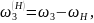
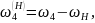
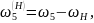
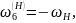
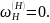
Передаточное отношение в обращенном механизме:
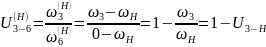
С другой стороны:
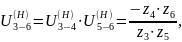
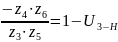
Тогда:
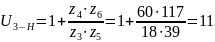
Таким образом, получаем общее передаточное отношение:
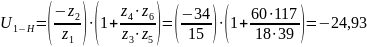
Отсюда
получаем
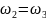 :
:
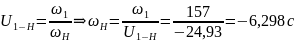
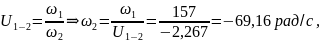
Чтобы найти
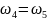 ,
определим передаточное отношение
,
определим передаточное отношение
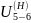 по способу Виллиса:
по способу Виллиса:
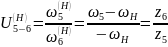
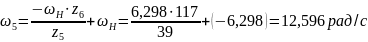
Расчитаем погрешность между аналитическим и графическим способами расчета угловых скоростей
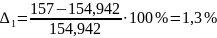
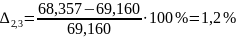
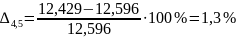
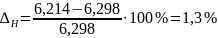
Сравнение угловых скоростей, полученных аналитически и графически, представлено в таблице 3.5
Таблица 3.5 – Сравнение данных аналитического и графического методов
Способ определения |
|
|
|
|
Аналитический |
|
|
|
|
Графический |
|
|
|
|
Расхождение, % |
1,3 |
1,2 |
1,3 |
1,3 |