- •Факультет інженерної механіки
- •1 Структурный и кинематический анализ рычажного механизма
- •Структурный анализ рычажногомеханизма
- •1.2 Построение планов механизма, скоростей и ускорений
- •2 Силовое исследование рычажного механизма
- •2.1 Определение масс звеньев, сил тяжести, и центральных моментов инерции
- •2.2 Определение сил реакций в кинематических парах и уравновешивающего момента методом академика Бруевича
- •3 Синтез зубчатого редуктора
- •3.1 Расчет геометрических параметров зубчатой передачи 1 – 2
- •3.2 Проверка качества зубьев и качества зацепления
- •3.3 Вычисление контрольных размеров
- •3.4 Построение эвольвентного зацепления
- •3.5 Подбор чисел зубьев колес планетарной передачи
- •3.6 Кинематическое исследование зубчатого редуктора двумя методами
- •4 Проектирование кулачкового механизма
- •4.1 Определение законов движения толкателя и построение их графиков
- •4.2 Построение профилей кулачка
1.2 Построение планов механизма, скоростей и ускорений
Строим 2
положениярычажного
механизмаконвейера – нулевое и
заданное (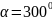 ).
).
Строим план скоростей. Для этого определяем угловую скорость кривошипа 1:
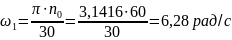
Скорость точки А:
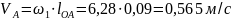
Определяем масштабный коэффициент:
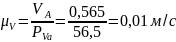
Скорость точки В:
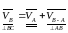
Определяем модуль скороститочкиB:
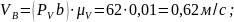
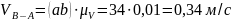
Определяем скорость
точки
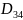 :
:
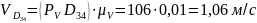
Определяем скорость
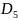 :
:
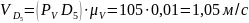
Построение плана ускорений
Ускорение точки А:
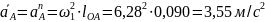
Выбираем отрезок для изображения ускорения точки А:
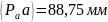
Тогда масштабный коэффициент ускорений:
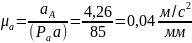
Строим план ускорений.
Определим ускорение точки В:
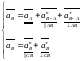
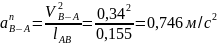
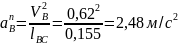
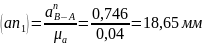
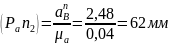
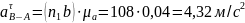
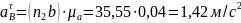
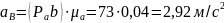
Определим ускорение точки D:
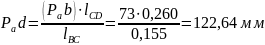
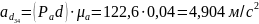
Определим ускорение пятого звена:
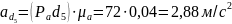
Определяем угловые ускорения звеньев:
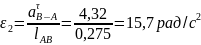
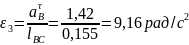
2 Силовое исследование рычажного механизма
2.1 Определение масс звеньев, сил тяжести, и центральных моментов инерции
Используя план ускорений для положения механизма, соответствующего угловой координате кривошипа , определим ускорения центров тяжести звеньев:
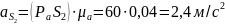
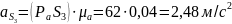
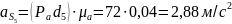
Определим массы звеньевпо формуле:
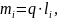
где
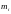 – масса i-го
звена;
– масса i-го
звена;
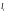 – длина i-го
звена;
– длина i-го
звена;
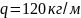 – масса одного метра звена.
– масса одного метра звена.
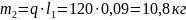
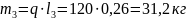
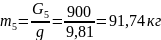
Определим центральные моменты инерции звеньев 2 и 3 по формуле:
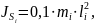
где
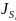 –
центральный момент инерции i-го
звена;
–
центральный момент инерции i-го
звена;
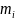 –
масса i-го
звена;
–
масса i-го
звена;
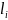 –
длина
–
длина
i-го звена.
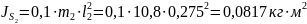
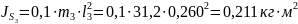
Определим силы
тяжести звеньев 2 и 3
по формуле
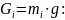
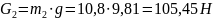
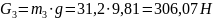
Определим силы инерции звеньев 2,3 и 5:
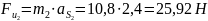
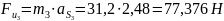
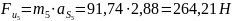
Определим моменты сил инерции звеньев 2 и 3:
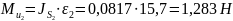
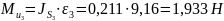
2.2 Определение сил реакций в кинематических парах и уравновешивающего момента методом академика Бруевича
Разбиваем механизм на структурные группы Ассура.
Рассматриваем в равновесии группу Ассура, состоящую из звеньев 4 и 5.
Принимаем
масштабный коэффициент
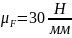 .
.
Строим
многоугольник сил 4 и 5 звеньев и из него
определяем реакции
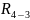 ,
,
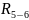 :
:
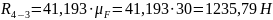
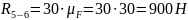
Рассматриваем в равновесии группу Ассура, состоящую из звеньев 2 и 3.
Силы
реакций в шарнирах A
и C
неизвестные по направлению разложим
на 2 составляющие:
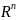 и
и
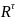 .
.
Составляем условие равновесия для второго звена:
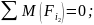
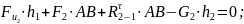
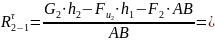
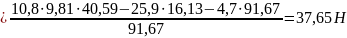
Составляем условие равновесия для третьего звена:
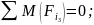
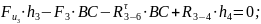
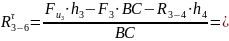
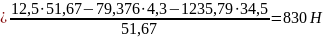
Принимаем
масштабный коэффициент
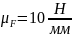 .
.
Строим
многоугольник сил второго и третьего
звеньев и из него определяем реакции
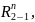
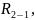
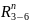 и
и
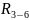 :
:
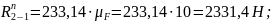
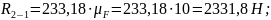
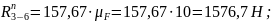
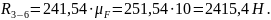
Рассматриваем в равновесии кривошип 1.
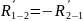
Определим уравновешивающий момент:
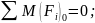
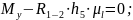
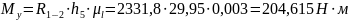
2.3 Проверка уравновешивающего момента методом М.Е. Жуковского
Все активные силы переносим в соответствующие точки повернутого на 90˚ плана скоростей.
Составляем уравнение равновесия полученного рычага:
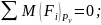
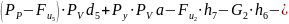
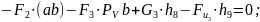
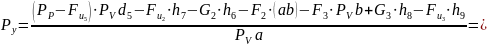
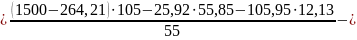
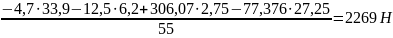
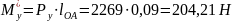
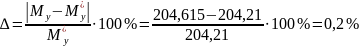
3 Синтез зубчатого редуктора
3.1 Расчет геометрических параметров зубчатой передачи 1 – 2
Исходные данные:
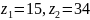 – числа
зубьев колес 1 и 2;
– числа
зубьев колес 1 и 2;
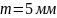 – модуль
всех колес;
– модуль
всех колес;
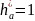 –
коэффициент
высоты головки зуба;
–
коэффициент
высоты головки зуба;
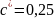 –
коэффициент
радиального зазора;
–
коэффициент
радиального зазора;
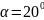 –
угол профиля
исходного контура.
–
угол профиля
исходного контура.
Параметры, не изменяющиеся в результате смещения
Шаг по делительной окружности:
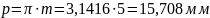
Радиусы делительных окружностей:
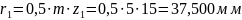
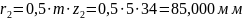
Радиусы основных окружностей:
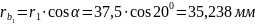
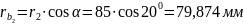
Шаг по основной окружности:
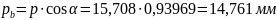
Расчет параметров для нулевого зацепления
Угол зацепления:
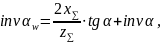
где
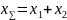 – суммарный коэффициент смещения;
– суммарный коэффициент смещения;
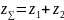 – суммарное число зубьев. Для нулевого
зацепления
– суммарное число зубьев. Для нулевого
зацепления
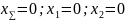 тогда:
тогда:
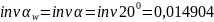
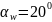
Радиусы начальных окружностей:
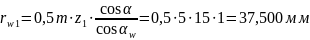
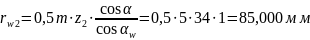
Межосевое расстояние:
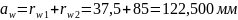
Радиусы окружностей впадин:
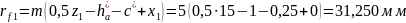
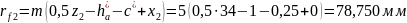
Высота зуба:
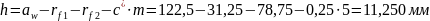
Радиусы окружностей вершин:
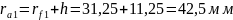
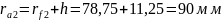
Толщина зубьев по делительным окружностям:
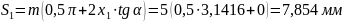
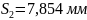
Расчет параметров для неравносмещенного зацепления
Угол зацепления:
где
– суммарный коэффициент смещения;
– суммарное число зубьев;
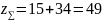 .
Для неравносмещенного зацепления
.
Для неравносмещенного зацепления
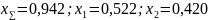 тогда:
тогда:
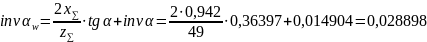
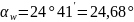
Радиусы начальных окружностей:
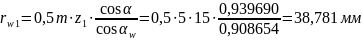
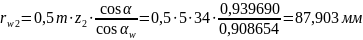
Межосевое расстояние:
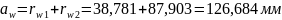
Радиусы окружностей впадин:
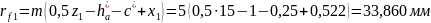
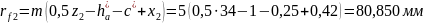
Высота зуба:
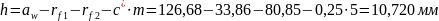
Радиусы окружностей вершин:
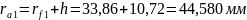
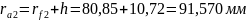
Толщина зубьев по делительной окружности:
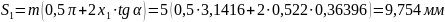
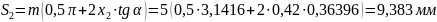
Толщина зубьев по основным окружностям:
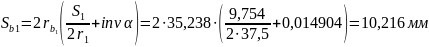
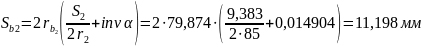
Толщина зубьев по начальным окружностям:
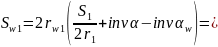
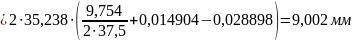
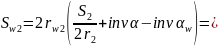
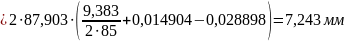
Шаг по начальной окружности:
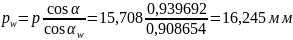
Проверка:
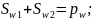
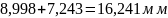
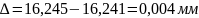
Определим углы профиля на окружностях вершин:
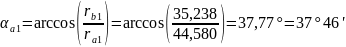
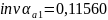
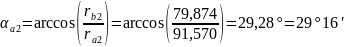
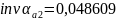
Толщина зубьев по окружностям вершин:
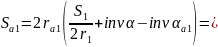
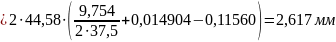
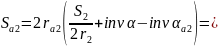
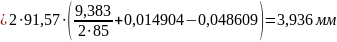
Коэффициент перекрытия:
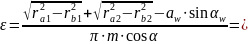
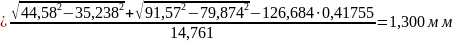
Таблица 3.1 – Расчетные параметры нулевого и неравносмещенногозацеплений
Тип зацепления |
Нулевое |
Неравно-смещенное |
|
Тип зацепления |
Нулевое |
Неравно-смещенное |
|
15 |
15 |
|
122,500 |
126,684 |
|
|
34 |
34 |
|
15,708 |
16,245 |
|
|
5 |
5 |
|
31,250 |
33,860 |
|
|
15,708 |
15,708 |
|
78,750 |
80,850 |
|
|
14,761 |
14,761 |
|
11,250 |
10,720 |
|
|
37,500 |
37,500 |
|
42,500 |
44,580 |
|
|
85,000 |
85,000 |
|
90,000 |
91,570 |
|
|
35,238 |
35,238 |
|
7,854 |
9,754 |
|
|
79,874 |
79,874 |
|
7,854 |
9,383 |
|
|
0 |
0,522 |
|
7,854 |
9,002 |
|
|
0 |
0,420 |
|
7,854 |
7,243 |
|
|
|
|
|
7,380 |
11,198 |
|
|
37,500 |
38,781 |
|
3,286 |
2,617 |
|
|
85,000 |
87,903 |
|
3,747 |
3,936 |
|
|
|
3,747 |
3,936 |
|||
|
1,581 |
1,300 |
||||

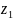
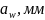
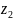
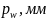
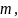 мм
мм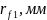
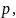 мм
мм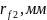
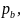 мм
мм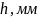
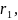 мм
мм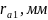
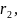 мм
мм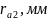
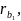 мм
мм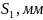
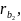 мм
мм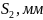
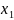
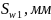
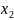
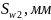
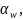 град
град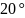
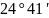
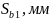
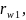 мм
мм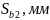
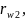 мм
мм