Билет №1

Направленными отрезками называют упорядоченную пару точек P и Q пространства. Первую из двух точек называют началом, другую концом направленного отрезка. Направленный отрезок по-другому называют вектор.

Начало вектора называют точкой его приложения. Вектор единичной длины называют ортом.

Вектор, начало, и конец которого совпадают, называют нулевым вектором. Обозначается как , точка А при этом любая. Направление нулевого вектора неопределенно. Расстояние между точками А и В называют длинной или модулем вектора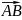 обычно обозначают .

Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.

Определение 6. Два вектора считаются равными, если они сонаправлены и равны по модулю.

Свойства отношения = между векторами:

1. (отношение рефлексивно)

2. Если , то = (отношение симметрично)

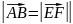3. Если и , то (отношение транзитивно ).

Величина отрезка-число равное длине, взятое с +, если отрезок совпадает с направлением оси и с – если нет.

При любом расположении точек АВС на оси выполняется следующее соотношение АВ+ВС=АС

Определение: Два вектора называются равными, если они: 1) коллинеарные; 2) равны по длине; 3) одинаково направлены.

Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными

Нулевой вектор считается коллинеарным любому вектору. Среди коллинеарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы. Векторы называются компланарными, если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости

Длина вектора.

Если задан модуль вектора, тогда проекция вектора на оси будет выражаться следующие образом:

Х= cosα

Y= cosβ

Z= cos λ

Cosβ=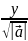

Cosλ=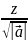

Cosα=

Линейные операции над векторами.

Суммой векторов А+В называют вектор С, который идет из начала А в конец В при условии, что В приложен к концу А

Разностью векторов В и А называют вектор, который в сумме с вектором А составит вектор В

Произведением α на вектор А называют вектор который коллинеарен (параллелен) и имеет длину и направлен так же как вектор А если α>0 и противоположно α<0.

Свойства линейных операций над векторами

1. Переместительное свойство

2. Сочетательное свойство

Чтобы построить несколько векторов а₁ а₂….а_n нужно к концу вектора а₁ приложить вектор а₂ и т. д.

Любой вектор можно выражать через единичные вектора

Билет №2

Определение.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

Линейная зависимость векторов  Определение. Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно ai , т.е. .  Если же только при ai = 0 выполняется , то векторы называются линейно независимыми.  Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.  Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.  Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.  Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.  Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.  Свойство 6. Любые 4 вектора линейно зависимы.

Определение. Система векторов называется линейно зависимой, если из этих векторов можно составить нулевую линейную комбинацию, когда хотя бы один из коэффициентов ее отличен от нуля.

Определение. Базисом в пространстве Rⁿ называется любая система из n-линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.      Пусть   – базис пространства Rⁿ и  . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что  .      Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора   в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца^[6].

• ложение и умножение на скаляр:

Или

или

а отсюда и вычитание и деление:

Или

или

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

• Скалярное умножение:

Или

(Только в прямоугольных координатах с единичным масштабом по всем осям).

• Через скалярное произведение - длину вычисление длины вектора

и угла между векторами

• Внешнее умножение:

для любой размерности пространства,

• Векторное умножение (только для трехмерного же пространства, на котором оно и определено):

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

Направляющие косинусы вектора 

a

 – это косинусы углов, которые вектор образует с положительными полуосями координат.

Чтобы найти направляющие косинусы вектора 

a

 необходимо соответствующие координаты вектора поделить на модуль вектора.

Свойство: Сумма квадратов направляющих косинусов равна единице.

Пусть дан вектор  ( _х, _у, _z).

Обозначим углы наклона этого вектора к осям Ох, Оу и Oz соответственно буквами   ,  и  . Три числа cos   , cos   и cos  принято называть направляющими косинусами вектора  . Полагая  =  (1; 0; 0) получаем из (9)

Аналогично

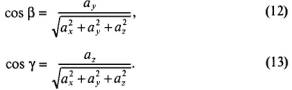
Из формул (11) - (13) следует:

1) сos²  + cos²   + cos²  = 1,

т.е. сумма квадратов направляющих косинусов любого ненулевого вектора равна единице;

т.е. направляющие косинусы этого вектора пропорциональны его соответствующим проекциям.

Примечание. Из формул (11)-(13) видно, что проекции любого единичного вектора   на оси координат соответственно совпадают с его направляющими косинусами и, следовательно,

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой.

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой  ), которая задаёт высоту точки над плоскостью.

Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат  , где   — расстояние до начала координат, а   и   — зенитный и азимутальный угол соответственно.

Билет №3

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

Скалярным произведением и называется число Скалярное произведение векторов

Свойства скалярного произведения

1. Перестановочное

а*в=в*а

2.Сочетательное

(α*а)*в=α*(а*в)

3. Распределительность относительно сложения

а*(в+с)=а*в+а*с

Геометрический свойства

Если составляют острый угол, то скалярное произведение больше 0

Если тупой, то меньше 0

Выражение скалярного произведения через координаты перемножающихся векторов

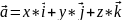
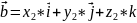
=x₁*x₂+y₁*y₂+z₁*z₂

Упорядоченная тройка некомпланарных векторов   в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой   от плоскости  , обход концов приведённых в общее начало   векторов   в указанном порядке кажется совершающимся в плоскости   по часовой стрелке. В этом случае наблюдателю, находящемуся с другой стороны от плоскости  , обход концов таких векторов будет казаться совершающимся против часовой стрелки.

B противном случае   — левая тройка.

 Под векторным произведением двух векторов   и   понимается вектор,   для которого:

-модуль равен площади параллелограмма, построенного на данных векторах, т.е.  , где  угол между векторами   и 

-этот вектор перпендикулярен перемножаемым векторам, т.е. 

-если векторы   неколлинеарны, то они образуют правую тройку векторов.

Смешанным (векторно-скалярным) произведением векторов   называется число, определяемое по формуле:  .

 Свойства смешанного произведения:

1.Смешанное произведение не меняется при циклической  перестановке его сомножителей, т.е.  .

2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е.  .

3.Необходимое и достаточное условие компланарности трех векторов  :  =0.

4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.  .

 Если известны координаты векторов  , то смешанное произведение находится по формуле: Угол между векторами — угол между направлениями этих векторов (наименьший угол).

По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними 

Условия ортогональности векторов. Два вектора 

a

 и 

b

 ортогональны (перпендикулярны), если их скалярное произведение равно нулю

a

 · 

b

 = 0

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Условия компланарности векторов

• Три вектора компланарны если их смешанное произведение равно нулю.

• Три вектора компланарны если они линейно зависимы.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.

Условия коллинеарности векторов

• Два вектора коллинеарные, если отношения их координат равны.

• Два вектора коллинеарные, если их векторное произведение равно нулю.

Билет 4

 в математике, система элементов a_ij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m × n)-матрице. Обозначения:

        

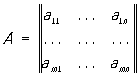
         или 

        Короче:

         М., состоящая из одной строки, называется строкой, из одного столбца — столбцом. Если m = n, то М. называется квадратной, а число n — её порядком. Квадратная М., у которой отличны от нуля лишь диагональные элементы α_i = α_ii называется диагональной и обозначается diag(α₁, ..., α_n). 

  Действия над матрицами. Произведением прямоугольной (m × n)-матрицы А на число ее называют М., элементы которой получены из элементов a_ij умножением на число α:

         

         Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть

         

         Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением (m × р)-матрицы А на (р × n)-матрицу В будет (m × n)-матрица С с элементами

         c_ij = a_i1b_1j + a_i2b_2j + ... + a_ipb_pj,

         i = 1, ..., m, j = 1, ..., n.

         Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA. Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой. Справедливы правила:

        

         Определитель произведения двух квадратных М. равен произведению определителей перемножаемых М.

         Часто удобно разбивать М. на клетки, являющиеся М. меньших размеров, проводя разделительные линии через всю М. слева направо или сверху вниз. При умножении такой так называемой клеточной М. на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М. осуществляются так, как будто вместо клеток стоят числа.

         Квадратная М. А = (a_ij) называется неособенной, или невырожденной, если её определитель не равен нулю; в противном случае М. называется особенной (вырожденной). М. А^-1 называется обратной к квадратной М. А, если AA^-1 = E, при этом  А есть необходимое и достаточное условие существования обратной М., которая при этом оказывается единственной и перестановочной с исходной М. Верна формула: (AB)^-1 = B^-1A^-1.

         Большой интерес приобретает обобщённая обратная (или псевдообратная) М. А⁺, определяемая как для любой прямоугольной М., так и для особенной квадратной. Эта М. определяется из четырёх равенств:

         AA⁺A = A, А⁺АА⁺ = А, AA⁺ = (AA⁺)*, А⁺А = (А⁺А)*.

Прямоугольная матрица - это матрица в которой число строк не равно числу столбцов.

a11	a12	...	a1n
a21	a22	...	a2n
...	...	...	...
am1	am2	...	amn

n = m

Квадратная матрица - это матрица с равным числом столбцов и строк.

1	0	...	0
0	1	...	0
...	...	...	...
0	0	...	1

Единичная матрица - это диагональная матрица, у которой каждый элемент на главной диагонали равен единице.

Над матрицами определена еще одна операция, называемая транспонированием.

        Определение 14.5   Пусть   -- матрица размеров   . Тогда транспонированной матрицей   называется такая матрица   размеров   , что   ,   ,   .         

Транспонированная матрица   обозначается   или   . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

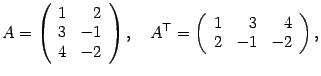
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij  b_ij

С = А + В = В + А.

             Операция умножения (деления) матрицы любого размера на произвольное число сводится к  умножению (делению) каждого элемента матрицы на это число.

 

 (А+В) =А  В

А() = А  А

 

Пример. Даны матрицы А = ; B = , найти 2А + В.

2А = ,                                 2А + В = .