Вопросы к коллоквиуму №1

1. Понятие высказывания

2. Логические операции

3. Формулы и таблицы истинности

4. Основные равносильности

5. Приложение алгебры высказываний

6. Понятие множества

7. Отношение между множествами

8. Операции над множествами и их свойства

9. Декартово произведение множеств

10. Диаграммы Эйлера - Венна

Контрольная работа №1

Образец решения и оформления контрольной работы Вариант 0

1. Построением общей таблицы истинности докажите равносильность формул

Решение. Равносильность двух формул имеет тогда и только тогда когда в таблице истинности, построенной сразу для обеих формул, столбцы значений истинности совпадают. Расставим порядок действий.

Составим таблицу истинности для этих формул.

p	q	r	1	2	3	4	5	6
и	и	и	и	и	и	и	л	и
и	и	л	и	и	и	и	л	и
и	л	и	л	л	л	и	л	л
и	л	л	л	и	л	и	л	л
л	и	и	и	и	и	и	л	и
л	и	л	и	и	и	л	и	и
л	л	и	и	л	л	и	л	л
л	л	л	и	и	и	л	и	и

Сравнивая столбцы 3,6 значений истинности формул, видим, что они совпадают, значит, формулы равносильны.

2. Переведите предложение на логический язык, постройте и сформулируйте его отрицание. «Если я пропустила занятия и не выполнила домашнее задание, то мне поставят двойку или пошлют в деканат за допуском».

Решение. Введем атомы p - я пропустила занятия, q – выполнила домашнее задание, r – мне поставят двойку, s – пошлют в деканат за допуском. Запишем предложение формулой, связывая атомы логическими операциями . Построим отрицание . Читаем: «Неверно, что если я пропустила занятия и не выполнила домашнее задание, то мне поставят двойку или пошлют в деканат за допуском». Используя законы логики высказывания, приведем формулу к более простому виду. Применим закон исключения импликации, закон де Моргана, закон двойного отрицания. . А значит, отрицание предложения формулируется так: «Я пропустила занятия и не выполнила домашнее задание и мне не поставят двойку и не пошлют в деканат за допуском»

3. Докажите и проиллюстрируйте кругами Эйлера

Решение. Построив картины Эйлера для обеих частей проверяемого равенства, убедимся, что они одинаковые, т.е. нет данных для построения контрпримера.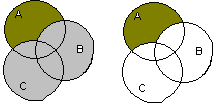 Докажем два встречных включения множеств и . Пусть х произвольный элемент множества М. Из определения разности множеств следует , но . Из определения объединения множеств следует, что и . Но так как , то по определению разности множеств и . Следовательно, х содержится в пересечении этих множеств, т.е. . Этим доказано, что произвольный элемент множества М является элементом множества S, т.е. . Докажем встречное включение. Пусть теперь . Из определения пересечения множеств следует, что и . Из определения разности множеств следует , но и . Из определения объединения множеств следует, что . Тогда определение разности множеств дает . Следовательно, произвольный элемент множества S является элементом множества М, т.е. . Два встречных включения дают равенство .

4. Найдите множество 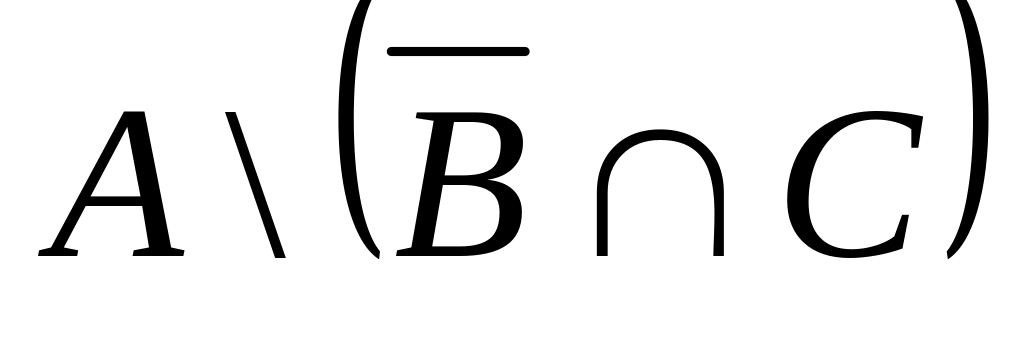, если А=(-;3), В=(2;7], C=(-5;10]

Решение. Расставим порядок действия в формуле .

Найдем дополнение

Найдем пересечение

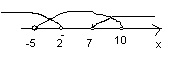
Найдем разность

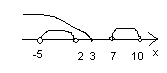
5. Найдите пересечение множеств А={3k/7 kZ}, B={2k/7 kZ}

Решение. По определению пересечения . Пусть х произвольный элемент, тогда по определению и . Т.е. х представим в виде дроби 3k/7 и 2k/7, а это значит, что в числителе должно стоять число которое делится как на три, так и на два, это число шесть. Т.о. АВ={6k/7 kZ}.