Метод Монтгомері

Розглянемо метод Монтгомері. Нехай з Позначимо Можна перевірити, що

(16.1)

Отже, знаючи - координати точок й , можна обчислити координати точок й , перейти до пари , або до пари . Кожна така ітерація вимагає одного подвоєння й одного додавання з використанням формули (16.1).

Після останньої ітерації, - координата точки може бути відновлена з - координати точки й - координат точок і по формулі

Використовуючи проективні координати, можна позбутися від інвертування, і кожна ітерація буде вимагати 6 множень. Усього ж трудомісткість алгоритму 5, що реалізує метод експоненціювання Монтгомері, дорівнює причому алгоритм не вимагає додаткової пам'яті на зберігання попередньо обчислених змінних, а час його роботи не залежить від значення

Алгоритм 5. Метод експоненціювання Монтгомері.

Вхід

Вихід

1.

2.

2.1.

3.1.

3.2.

4.

Алгоритм 5 вимагає однієї інверсії, а не двох, тому що можна обчислити

, а потім одержати множенням на . Можна домогтися істотного збільшення продуктивності, якщо операцію подвоєння замінити операцією ділення точки на два. Виграш до 40% при цьому досягається у зв'язку з відсутністю операції інверсії елемента в полі. Крім того, групові операції послідовних ділень у НБ зводяться практично до однієї операції множення в полі.

Методи експоненціювання при фіксованій точці

Фіксованою точкою в криптосистемі завжди є генератор або базова точка криптосистеми порядку . Такі точки – це відкриті ключі користувачів. Якщо в системі є резерв пам'яті, його можна використати для зберігання заздалегідь розрахованих точок. Наприклад, якщо обчислити й записати в пам'яті точки , то для визначення скалярного добутку залишиться лише обчислити суми точок відповідно до двійкового подання . У середньому для цього буде потрібно лише операцій. Їхнє число можна зменшити до операцій додавання й вирахування, якщо скористатися трійковим поданням .

Другим досить витонченим підходом є підхід на основі вікон з фіксованою базою. Замість двійкового подання числа використається -ічне із предобчислюванням точок . Дійсно, нехай -ічне подання числа має вигляд

Тоді

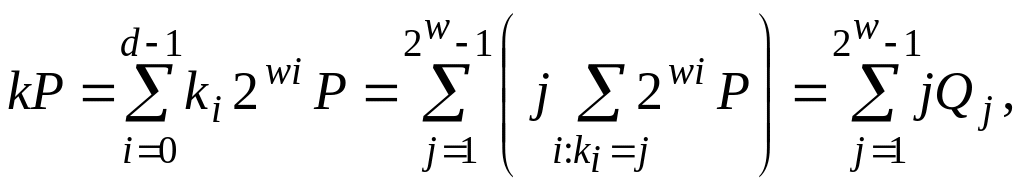
де

Ці обчислення здійснюються за допомогою наступного алгоритму.

Алгоритм 6.

Вхід ширина вікна , ,

Вихід

1. Предрозрахунки

2.

3.

3.1

3.2.

4.

Середня обчислювальна складність алгоритму оцінюється числом додавань 

Метод вікон у цьому випадку більше продуктивний, чим при невідомій точці, тому що предрозрахунки не входять в алгоритм експоненціювання. Якщо використати поряд з додаванням подвоєння точки, реалізувати алгоритм можна інакше. Два вікна точки шириною кожне можна представити у вигляді



Всі можливі точки й обчислюються на етапі предрозрахунків і записуються на згадку. Загальне число цих точок росте експоненційно зі збільшенням ширини вікна . Двійкове подання точки розбивається далі на фрагментів шириною . У кожному такому фрагменті відбираються старші розряди й розряди зі зрушенням вправо на

( тобто на половину фрагмента). Їхні двійкові подання дають першу пару точок й , які складаються, після чого їхня сума подвоюється. Далі реалізується алгоритм послідовних додавань і подвоєнь праворуч із двома вікнами, описаний нижче.

Алгоритм 7.

Вхід ширина вікна , , ,

Вихід

1. Предрозрахунки обчислити всі точки й ,

2. Представити число у вигляді конкатенації фрагментів шириною

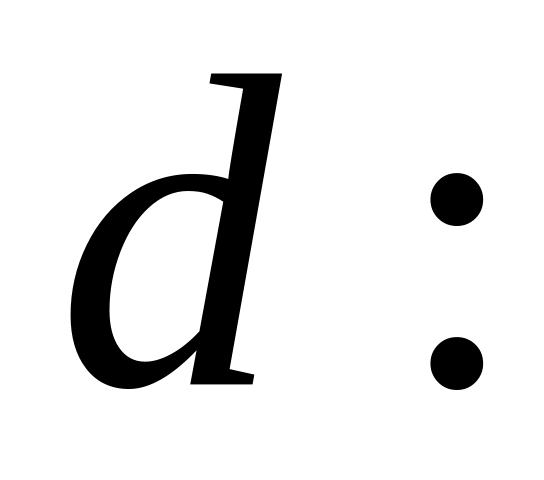
Нехай означає - й біт фрагмента

3.

4.

4.1.

4.2.

5.

Обчислювальна складність цього алгоритму оцінюється числом групових операцій

Обмінюючи час обчислень на пам'ять, можна й далі підвищувати продуктивність експоненціювання точки кривої. Наприклад, для кожного вікна шириною можна заздалегідь розрахувати точок, при цьому на згадку прийдеться записати точок. Операція подвоєння в цьому випадку не використається, а складність оцінюється числом додавань. Цей алгоритм назвемо алгоритмом максимальної пам'яті. У табл. 13.1. дані для порівняння величини пам'яті й тимчасової складності ( числа групових операцій) алгоритму 6 й алгоритму максимальної пам'яті при . В обох випадках з ростом ширини вікна збільшується пам'ять і знижується число групових операцій. Очевидно, що останній алгоритм при наявності більших резервів пам'яті дозволяє істотно прискорити операцію експоненціювання фіксованої точки

Таблиця 16.1  Об'єм пам'яті й тимчасова складність ( число групових операцій)алгоритму 6 й алгоритму максимальної пам'яті при

Метод	W = 3		W = 4		W = 5		W = 6
	M	S	M	S	M	S	M	S
Алгоритм 6	14	900	30	725	62	632	126	529
Алгоритм максимальної пам'яті.	469	58	750	46	1280	38	2079	33

Контрольні запитання та завдання

1. Яка сутність алгоритму подвоєння – додавання експоненціювання точки кривої

2. Яка сутність алгоритму подвоєння – додавання – вирахування експоненціювання точки кривої

3. Наведіть метод вікон з алгоритмом подвоєння – додавання – вирахування експоненціювання точки кривої.

4. Яка сутність методу Монтгомері експоненціювання точки кривої

5. Оцініте складність алгоритму експоненціювання точки кривої.