Лекція 11 Складність алгоритмів факторизації.

План

1. Алгоритм Бриллхарда-Моррисона та його складність.

2. Метод квадратичного решета та його складність.

3. Двійкове решето.

Алгоритм Бриллхарда - Моррисона.

Сутність алгоритму Бриллхарда-Моррисона , опублікованого ними в 1975 р., полягає у двох змінах в алгоритмі Діксона:

1. Випадкові числа вибираються за допомогою методу безперервних дробів, запропонованого Лагранжем, що дозволяє генерувати такі , що є малим, і тому імовірність його розкладання більш висока;

2. З факторної бази виключаються ті числа , для яких

Розглянемо алгоритм більш докладно.

Теорема 1. Нехай  дійсне число, і  послідовність його підхідних дробів, Тоді при всіх виконується нерівність

Д о в е д е н н я. У силу властивостей підхідних дробів маємо

Звідси

Наслідок. Нехай не є квадратом й  підхідний дріб для числа . Тоді мінімальний за абсолютною величиною лишок дорівнює й не перевершує

Д о в е д е н н я. Відповідно до властивостей порівнянь маємо

,

причому в силу теореми 7, Л-6, ТЧ справедлива нерівність Тому мінімальний за абсолютною величиною лишок числа за модулем збігається з , що й було потрібно довести.

Даний наслідок показує, що якщо як випадковими числами на першому етапі алгоритму Діксона брати числа , то мінімальний за абсолютною величиною лишок числа , який дорівнює , не буде перевищувати значення . Тому імовірність його розкладання в добуток чисел бази буде більше високою, чим при випадковому виборі.

В цей алгоритм згодом внесли ряд удосконалень замість можна розкладати в безперервний дріб число , де маленький множник підбирається так, щоб у базу множників увійшли всі малі прості була запропонована також так звана стратегія раннього обриву й т.д. Складність цього алгоритму була оцінена в 1982 р. величиною При доведенні цієї оцінки використовувався ряд правдоподібних, але не доведених гіпотез про розподіл простих чисел. Це субекспоненційна складність.

Метод квадратичного решета.

В 1981 році К. Померанц запропонував для породження -чисел використати підхід, що узагальнює метод Ферма .

Розглянемо функцію

,

яка є квадратним тричленом із цілими коефіцієнтами.

При кожнім цілому виходить нетривіальне порівняння

,

причому значення при малих невелике:

і тому

Отже, якщо замість випадкових чисел в алгоритмі розглядати значення при випадкових , що попадають у деякий інтервал , то імовірність породження -чисел зростає. При цьому можна попередньо здійснити просіювання тих із цього інтервалу, які можуть давати розкладання на множники з факторної бази Для цього для кожного , котре може виступати як співмножник у розкладанні

вирішується квадратне рівняння

у кільці . Якщо  розв’язання цього рівняння, то повинна виконуватися рівність

Проробивши попередньо роботу по знаходженню коренів для кожного , можна тепер залишити в інтервалі тільки ті числа , для яких порівняння виконується для досить великої кількості чисел . Знання для кожного списку тих , для яких виконуються ці порівняння, допоможе також швидше здійснити факторизацію числа якщо вона існує.

Дж. Девіс і П. Монтгомері узагальнили даний підхід . Вони запропонували використати многочлен

де коефіцієнти є цілими числами і задовольняють умові

;

При такому виборі коефіцієнтів виконується рівність

звідки отримуємо порівняння

причому

Коефіцієнти вибираються, виходячи з наступних міркувань. Функція приймає максимальне значення на кінцях відрізка

Мінімальне значення вона приймає в точці , :

Будемо вибирати так, щоб максимальне й мінімальне значення функції на відрізку були рівні за абсолютними значеннями і протилежними за знаком (рис.11.1)

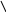
f(x)

М

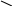
М x

Рисунок 11.1  Геометрична інтерпретація метода квадратичного решета (Померанца).

Тому вважатимемо:

Число знаходимо як розв’язання порівняння

Нарешті, число вибираємо з умови

Зазначимо, що умову існування розв’язання другого порівняння можна перетворити в такий спосіб: для всіх простих дільників виконується співвідношення Знання розкладу числа необхідно також тому, що воно бере участь як співмножник у шуканому порівнянні. Тому, звичайно, як число вибирають або повний квадрат, або число, яке факторизується в добуток простих чисел з факторної бази. При даному виборі параметрів значення багаточлена на інтервалі задовольняє нерівності

що в раз краще, ніж у вихідного алгоритму Померанця, у якому при

Тому такі поліноми більш підходять для пошуку -чисел.

Метод Померанця називається методом квадратичного решета або -методом, а метод Девіса-Монтгомері  -методом (multiply polino-mial variation of quadratic sieve algorithm ).

Розглянемо для приклада двійкове решето, що відповідно до сучасних поглядів є найбільш швидким при довжині модуля не більше 120 десяткових цифр.

Сутність методу:

Нехай та  цілі числа, такі, що:

. (11.1)

Представимо (11.1) у вигляді

З урахуванням того, що операція модульна, маємо

(11.2)

Розкладемо (11.2) у різницю квадратів, одержимо

(11.3)

причому

Вираз (11.3) означає, що можливі чотири варіанти:

У випадку 1 й 2 або знайти неможливо. У випадку 3 і 4 є розв’язання.

Якщо , то ми можемо використати алгоритм Евкліда й обчислити найбільший загальний дільник:

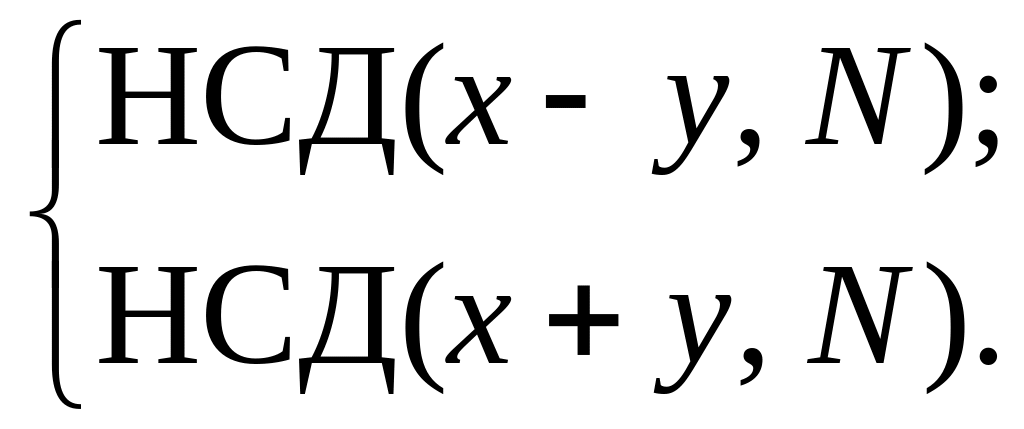(11.4)

Вираз (11.4) дозволяють знайти або .

Наведемо стислу сутність алгоритму двійкового решета.

1. Нехай  число, яке необхідно факторизувати. Побудуємо деяку базу , з такими значеннями, щоб , де  прості числа невеликого розміру,  база двійкового решета.

2. Знайдемо , округливши результат знизу. Побудуємо числа виду і знайдемо В результаті одержимо рівняння:

Таким чином, ми маємо

Складність оцінюється такою же функцією як у методі безперервних дробів, але замість константи 1,5 отримано кращу  .

Н а п р и к л а д. Нехай Факторизуємо , використовуючи метод двійкового решета .

Побудуємо базу

Знайдемо Результати запишемо в таблицю 11.1.

Таблиця 11.1 – Результати розрахунків

I			2	3	5	7
1 2 3 … … 16	1+14=15 16 17 30	47	4 - 4 6	- - - -	- - 1 -	- - - -	+ - + +

Ми знайшли два числа й таких, що

.

Знайшовши НСД для , маємо

НСД

Значить . Далі можна знайти

На практиці при великих матриця таблиці має дуже великий розмір. Так для таблиця має розмір При використанні метода квадратичного решета теж приходять до матриці великого розміру. Потім, комбінуючи рядки, у яких розкладання за базисом здійснилося, можна домогтися, щоб , знайшовши за такий спосіб і .

Для двійкового й загального решета числового поля складність криптоанализа оцінюється як:

і  параметри методу. Наприклад, для квадратичного решета

Контрольні питання

1. Яка сутність методу квадратичного решета

2. Оцініть складність методу квадратичного решета.

3. Яка сутність методу двійкового решета та як оцінити його складність

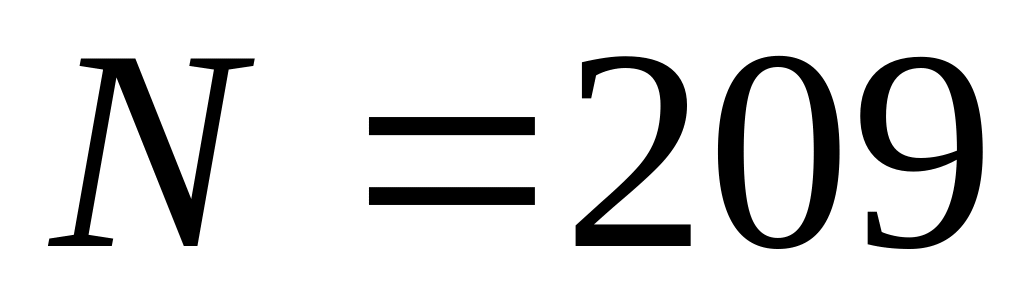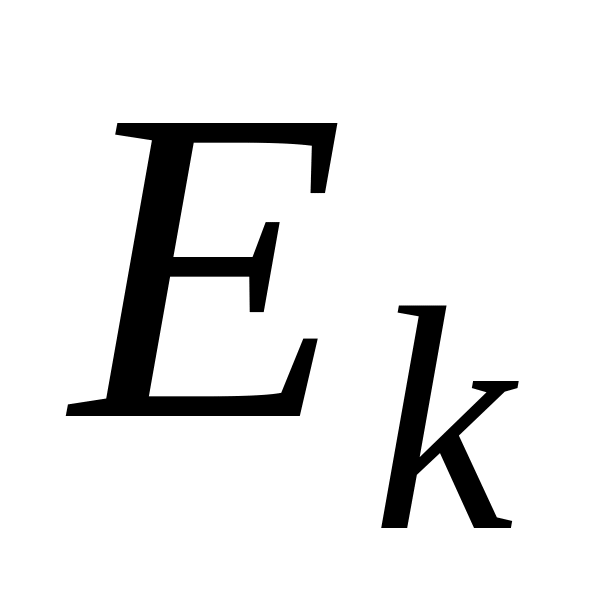4. Нехай відомо, що в криптосистемі використовується відкритий ключ а модуль перетворення . Необхідно знайти секретний ключ й оцінити складність криптоанализу методом квадратичного решета.