Министерство образования Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

Московский государственный технологический

университет "СТАНКИН"

Егорьевский технологический институт (филиал)

ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ БИНОМИНАЛЬНОГО РАСПРЕДЕЛЕНИЯ.

Методические указания

к выполнению лабораторной работы

ЕТИ.ПМ.01

Егорьевск 2012

Составитель: кандидат физ.-мат. наук, доцент Бармакова Т.В.

Рецензент__________________________________________________

Данные указания предназначены для студентов, обучающихся по специальности 120100. В методических указаниях приведено содержание и изложен порядок выполнения лабораторной работы № 2 по теме «Предельные распределения для биноминального распределения».

Методические указания рассмотрены и одобрены кафедрой естественнонаучных дисциплин

Протокол № от

Зав. кафедрой ________________А.П. Нилов

Методические указания рассмотрены и одобрены методическим советом института

Протокол № от

Председатель совета_______________ Семенов А.Д.

Предельные распределения для биноминального распределения.

Цель работы: а) изучить точность вычисления вероятностей в схеме Бернулли с помощью приближенных формул Пуассона, Муавра-Лапласа, б) изучить возможности программы Mathcad при решении задач теории вероятностей, связанных со схемой Бернулли.

Краткие сведения из теории. Теорема Пуассона.

При большом количестве испытаний вычисления по формуле Бернулли становятся затруднительными. Однако в ряде случаев их можно заменить более простыми асимптотическими формулами. Одна из основана на теореме Пуассона, утверждающей следующее. Если число испытаний n   и р  0 так, что np, >0 , то . Это означает, что при больших n и малых р вместо вычислений по точной формуле

можно пользоваться приближенной формулой

В Mathcad для вычисления плотности вероятности и функции распределения случайной величины, имеющей биноминальное распределение, предназначены функции dbinom(k,n,p) и pbinom(k,n,p) , значения которых – соответственно равны и F(k).

В Mathcad для вычисления вероятности случайного значения и функции распределения случайной величины, имеющей пуассоновское распределение, предназначены функции dpois(k, ) и ppois(k, ) , значения которых – соответственно равны и F(k).

Пояснения к заданию №1

Исследуйте для приведенного в задании эксперимента точность асимптотической формулы Пуассона.

Порядок выполнения задания.

1. Вычислите требуемые вероятности по формуле Бернулли.

2. Вычислите требуемые вероятности по формуле Пуассона.

3. Сравните полученные результаты.

Пример выполнения задания.

В здании 1000 лампочек. Вероятность р выхода из строя одной лампочки в течение года равна 0.003. Найдите вероятность того, что в течение года выйдет из строя не менее трех ламп, используя формулу для биномиального распределения и по приближенной формуле Пуассона для случайной величины  , имеющей распределение Пуассона с параметром . Здесь  -- случайная величина, значения которой равны числу ламп, вышедших из строя в течение года. Для сравнения вычислите по формуле Бернулли и по формуле Пуассона для вероятность того же события , когда в здании 10 лампочек и вероятность р отказа в течение года для одной лампочки равна 0.2. Сравните результаты.

Фрагмент рабочего документа Mathcad с решением задачи приведен ниже.

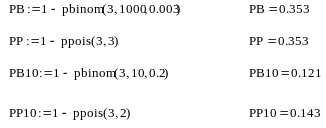
Из приведенных вычислений видно, что в первом случае (n=1000, p=0.003 ) результаты вычислений по точной и асимптотической формулам совпадают, а во втором (n=10, p=0.2) отличаются.

Локальная формула Муавра-Лапласа.

На практике пуассоновским приближением пользуются при . Если , то для расчетов используют приближение в соответствии с теоремой Муавра-Лапласа.

Пусть 0<p<1 и величина ограничена при , тогда

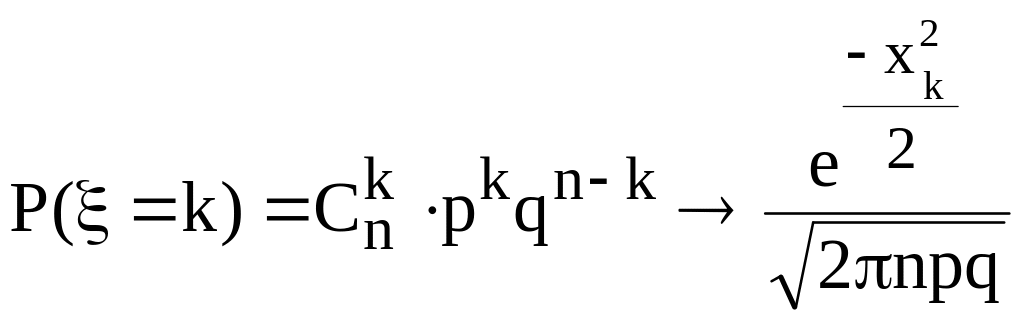
Требование ограниченности величины означает, что при величина k тоже должна расти вместе с величиной n. Точность формулы

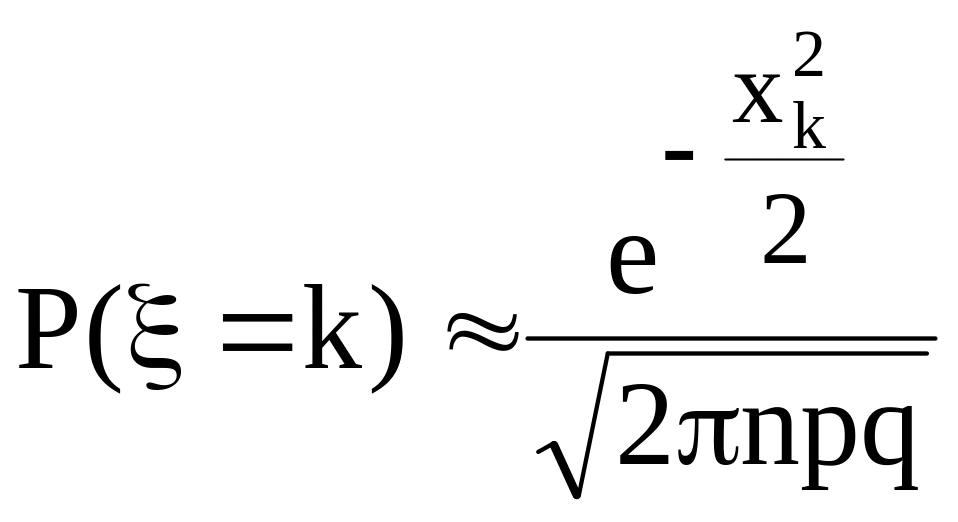
растет как с ростом величин n и k , так и по мере приближения величин p и q к .