Вариант 1
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = cosx + y2, y(0) = 1
5. На интервале (-π; π) задана периодическая с периодом 2π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
f(x) = x2
Вариант 2
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = ex + y2, y(0) = 0
5. На интервале (-π; π) задана периодическая с периодом 2 π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
f(x) = | sinx |
Вариант 3
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
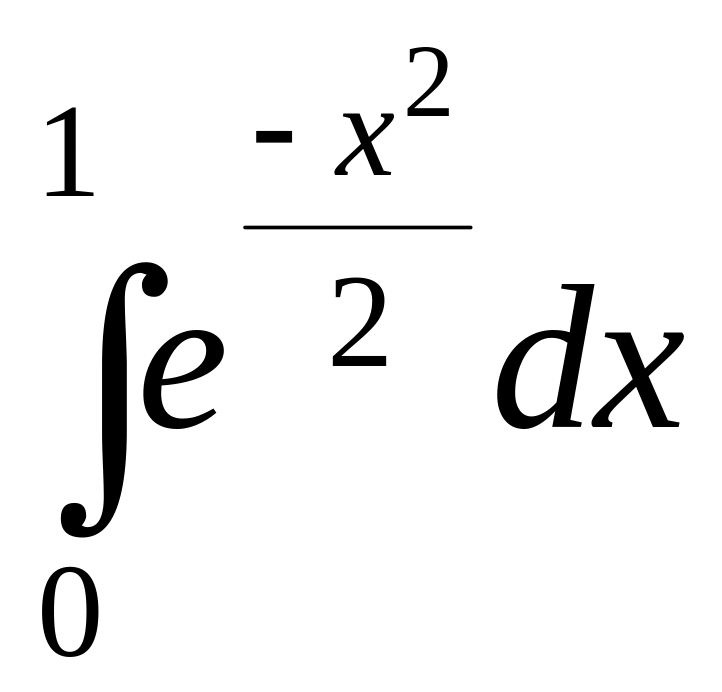
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = y + y2, y(0) = 3
5. На интервале (-π; π) задана периодическая с периодом 2 π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
Вариант 4
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = 2ey –x ∙y, y(0) = 0
5. На интервале (-π; π) задана периодическая с периодом 2 π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
f(x) = | x |
Вариант 5
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = sinx + y2, y(0) = 1
5. На интервале (-π; π) задана периодическая с периодом 2 π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
f(x) = x
Вариант 6
1. Исследовать на сходимость следующие числовые ряды:
a.
b.
c.
2. Найти интервал сходимости степенного ряда:
3. Вычислить определенный интеграл с точностью до 0,001:
4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию y(0) = y0:
y' = ex + y, y(0) = 4
5. На интервале (-π; π) задана периодическая с периодом 2 π функция f(x). Требуется разложить f(x) в ряд Фурье в тригонометрической и комплексной формах:
f(x)
=
– x