6. Однаково розподілені доданки.
6.1. Різнорозподілені доданки
Розглянемо суму
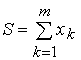(5.12)
шести (m = 6) незалежних випадкових величин, що мають beta-розподіл з параметрами a=b=0.5, щільність якого
,
(5.13)
де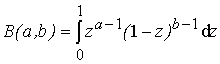 
-
beta-функція. Щільність при обраних
значеннях параметрів має U-подібний
вигляд, дуже далекий від нормального;
переконаємося в цьому, побудувавши
графік щільності .
Щоб статистично оцінити закон розподілу для суми S, слід багаторазово, N раз (наприклад, N=500), промоделювати підсумовування: одержимо S1, S2,...,SN - вибірку для суми; для цієї вибірки побудуємо гістограму і порівняємо її візуально з нормальною щільністю.
6.1. Різнорозподілені доданки
Розподіл суми збігається до нормального закону й у тому випадку, коли доданки розподілені за різними законами.
Завдання
1.
Оцінити експериментально розподіл
для сум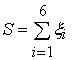и 
шести
доданків, розподілених за різними
законами; вибрати їх із сімейства
beta-розподілів (5.13), задавши наступні
параметри:
-
1
2
3
4
5
6
a
1
0.5
1
1
2
2
b
0.5
1
1
2
1
2
Згенерувати вибірку для суми і побудувати гістограму для неї. Переконатися в тім, що розподіл близький до нормального. Роздрукувати гістограми для доданків і для суми.
Якщо ж у сумі (5.12) є доданок, дисперсія якого істотно перевищує всі інші, то наближена нормальність місця не має.
Завдання 2. Перевірити це (одержати гістограму), додавши в (5.12) 7-і доданок, що має beta-розподіл з параметрами a=b=0.5 і помножений на 1000.
Додаток 1 Системні змінні
Нижче наведені системні змінні і константи Mathcad з їхніми значеннями за замовчуванням.
= 3.14159 |
Число . Щоб надрукувати натисніть [Ctrl-P] |
e = 2.71828 |
Основа натурального логарифма |
|
Нескінченність (10307). Щоб надрукувати, натисніть [Ctrl-Z] |
% |
Відсоток. Використовуйте його у виразах, подібних 10% чи як множник, що маштабується. |
I |
Уявна одиниця |
j |
Уявна одиниця |
TOL =10-3 |
Припустима погрішність при різних алгоритмах апроксимації (інтегрування, розв’язок рівнянь). Змінити значення системної змінний TOL і нижче наступних можна за допомогою команди МатематикаПараметри. |
CTOL = 10-3 |
Установлює точність обмежень у блоці розв’язку, щоб розв’язок був припустимим. |
ORIGIN = 0 |
Визначає індекс першого елемента векторів і матриць. |
FRAME = 0 |
Використовується як лічильник при створенні анімацій. |
PRNPRECISION = 4 |
Число значущих цифр. |
PRNCOLWIDTH = 8 |
Число позицій для числа. |
CWD |
Поточний робочий каталог у формі рядка. |