Эффект диверсификации
Мы рассмотрели портфель, состоящий из двух активов, и сделали общие выводы относительно его формирования. Они верны и для портфеля, сформированного из нескольких активов.
Перепишем формулу 6.8, заменив индекс i на k:
,
(6.13)
где αk - вес k -го актива в портфеле из n активов; rk – доходность k -го актива, %.
Дисперсия доходности портфеля в общем виде вычисляется по формуле:
.
(6.14)
где - коэффициент корреляции между активами i и k.
Дисперсия портфеля является функцией дисперсий индивидуальных активов и по парной корреляции между ними. В общем виде формула дисперсии принимает вид:
.
(6.15)
Рассмотрим портфель – с равными долями активов:
αi = αk = 1/n.
Тогда
первая часть суммы, составляющей
,
будет равна:
.
Очевидно,
что
при
,
где σ2max – максимальная из дисперсий активов, составляющих портфель.
Таким образом, при включении дополнительного актива в большой портфель дисперсия его доходности практически не играет роли – важна только средняя ковариация доходности этого актива с доходностью других активов портфеля.
Явление снижения дисперсии портфеля при объединении значительного числа активов называется эффектом диверсификации. Проиллюстрируем его на результатах моделирования стандартного отклонения портфеля акций, расширяемого за счёт добавления по одной случайным образом выбранных акций к уже имеющимся – с равными весами.
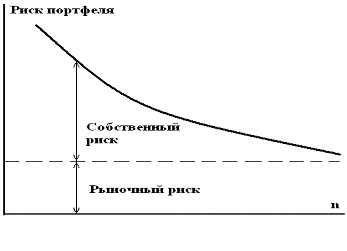
Рис. 6.6. Зависимость риска портфеля от числа входящих в него активов
На рис. 6.6 показано, как повышение уровня диверсификации (увеличение n - числа различных активов в портфеле) уменьшает портфельный риск, и его значение довольно быстро стремится к асимптотическому значению, равному корню квадратному из средней ковариации. Вложение инвестиций в более чем 50 разных активов уменьшает риск только немного ниже уровня риска для портфеля с 30 видами активов. Из этого следует, что не следует формировать портфель из сотни различных активов, поскольку риск портфеля снизится на очень незначительную величину, а управление таким портфелем потребует значительных средств и многократно усложнится.
Диверсификация позволяет снизить только величину несистематического риска, который обусловлен индивидуальными особенностями отдельного эмитента. Величина систематического риска для реальных портфелей не снижается путем диверсификации, поскольку этот вид риска зависит от стабильности развития экономики и ряда макроэкономических показателей. Чем выше стабильность, тем ниже систематический риск.
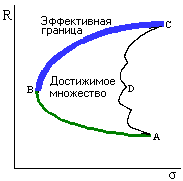
Эффективная граница и оптимальный портфель
Если взять некоторое число активов, присутствующих на рынке, и все возможные их комбинации (портфели), на плоскости "доходность – риск" мы получим допустимое множество портфелей, подобное тому, которое изображено на рис. 6.6. Множество портфелей будут расположено в рамках фигуры ABCD.
|
Рис. 6.6. Допустимое множество портфелей
Марковиц показал, что такое множество имеет вид «зонтика».
Рациональный инвестор будет стремиться минимизировать свой риск и увеличить доходность. Поэтому всем возможным портфелям допустимого множества вкладчик предпочтет только те, которые расположены на отрезке ВС, поскольку они являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью. Набор портфелей на отрезке ВС называют эффективной границей - это набор доминирующих портфелей.
Эффективная граница является выпуклой кривой. При объединении в портфель каждой пары активов линия на плоскости "доходность – риск", соответствующая разным соотношениям весов, будет проходить левее и выше прямой, соединяющих соответствующие точки, при объединении пар таких портфелей в новый портфель – еще левее и выше, и т. д., а эффективная граница будет огибающей множества всех таких линий.
Если портфель лежит ниже эффективной границы, то за счет дополнительной диверсификации можно повысить его доходность, не повышая риск.
Каждая точка эффективной границы соответствуют эффективному портфелю. Портфель является эффективным, если никакой другой портфель не обеспечивает более высокую ожидаемую доходность при том же уровне ожидаемого риска, или более низкий риск при том же уровне доходности.