6.3. Выбор портфеля на основе подхода «доход - риск»

«Ни один бизнес не обходится без

решений и принимать их следует в

системе, дабы иметь хотя бы один шанс на

то, чтобы оказаться правым».

Питер Ф. Драккер

Началом современной теории портфельных инвестиций считается 1952 г., когда появилась статья Г. Марковица (Harry Markovitz) под названием "Выбор портфеля". В этой статье впервые была предложена математическая модель формирования оптимального портфеля ценных бумаг и методы построения таких портфелей на основе теоретико-вероятностной формализации понятия ожидаемой доходности и риска. Применение вероятностных методов позволило существенно продвинуться в исследовании влияния риска на принятие инвестиционных решений.

Упрощенная модель: портфель из двух активов

Концепция диверсификации инвестиций определяется следующим простым выражением: "Не кладите все ваши яйца в одну корзину". Диверсификация означает вложение капитала, по крайней мере, в два различных актива. Если все ваши деньги инвестируются в один рисковый актив, норма доходности ваших инвестиций зависит исключительно от того, какова будет рыночная стоимость этого актива и чему будет равна величина полученного дохода от владения этим активом. Если вы вкладываете свои денежные средства в два различных актива, и оба характеризуются высоким уровнем риска, то вы можете получить низкий доход на вложенный капитал или можете даже понести существенные убытки.

Используя половину денежных средств для покупки одного актива, а другую половину – для покупки другого актива, можно снизить величину риска в целом для инвестированного капитала в сравнении с вариантом вложения капитала на покупку какого-нибудь одного актива. Это обусловлено тем, что низкий уровень дохода, получаемого по одному активу, может компенсироваться высоким доходом, получаемым по другому активу.

При диверсификации инвестиций за счет формирования портфеля ценных бумаг ожидаемая доходность портфеля определяется из выражения:

, (6.8)

где α_i – доля инвестиций, вложенный в i- ый актив, доли ед.; r_i – ожидаемая норма доходности i – го актива, % в год; n – число различных активов в портфеле.

Ожидаемая норма доходности портфеля с ценными бумагами представляет собой средневзвешенную ставку доходности на основе доходности отдельных видов ценных бумаг, лежащих в основе портфеля. В качестве весов выступают доли каждого вида ценных бумаг в портфеле.

Уровень риска при формировании портфеля из акций двух компаний можно определить из следующего выражения:

, (6.9)

где α₁ – доля средств, вложенная в акции первой компании; α₂ – доля средств, вложенная в акции второй компании; σ₁ – уровень риска для акций первой компании; σ₂ – уровень риска для акций второй компании; - коэффициент корреляции между ожидаемой доходностью акций первой и второй компаний.

Пример 6.2. Вы решили вложить 100000 руб. в покупку акций компаний А и В. Компания А выпускает купальники, солнечные зонты и другие изделия, необходимые при жарком лете. Компания В выпускает изделия (зонты, плащи и др.), которые необходимы при холодном и дождливом лете. При жаркой летней погоде потребители будут покупать летние изделия, и прибыль компании А увеличится, что будет способствовать росту доходности акций этой компании. Если лето будет дождливым и холодным, то увеличится спрос на изделия компании В, и можно ожидать, что доходность акций компании В возрастет.

Предположим, что вероятности наступления холодного или жаркого лета равны 0,5. При жарком лете доходность инвестиций вложенных в акции компании А будет равна 50 % в год, а доходность акций компании В составит (-20 %) в год. Если же лето будет холодным и дождливым, то мы будем иметь обратную картину: доходность акций компании А составит (-20 %), а доходность акций компании В будет равна 50% в год. Показатель, выражающий меру тесноты связи совместного движения нормы доходности акций компаний А и В, называется коэффициентом корреляции, который численно изменяется в пределах от -1 до +1. В нашем примере коэффициент корреляции примем равным (-1), поскольку доходности акций компаний А и В изменяются в обратной зависимости, то есть при увеличении доходности одной акции доходность другой акции снижается и наоборот.

Перед инвестором стоит выбор: вложить свои свободные денежные средства в акции компании А или компании В? Оба варианта вложения средств могут обеспечить доходность инвестиций в размере 50 % в год с вероятностью 0,5 и с такой же степенью вероятности – принести убыток в размере 20 % в год.

Если инвестор диверсифицирует свои вложения путем покупки акций обеих компаний, то риск потерь может быть сведен к нулю. Но уровень доходности его инвестиций также снизится, что видно из следующих расчетов.

Пример 6.3. Инвестор решил вложить половину своих свободных денежных средств в акции компании А, а другую половину – в акции компании В. В этом случае уровень доходности его инвестиций будет следующим (табл. 6.4):

Таблица 6.4

Ожидаемая доходность инвестиций при диверсификации их вложений

Характер лета	Вероятность	Норма доходности, %
		Инвестирование в акции А	Инвестирование в акции В	Инвестирование в акции А и В
Жаркое	0,5	50	-20	15
Холодное	0,5	-20	50	15

При диверсификации инвестиций ожидаемая норма доходности капитала при наступлении жаркого лета будет равна:

R_Port = 50 × 0,5 + (-20) × 0,5 = 15 %.

Инвестор будет иметь это же значение ожидаемой нормы доходности и при наступлении холодного лета:

R_Port = (-20) × 0,5 + 50 × 0,5 = 15 %.

На основе формулы 6.9 определим влияние диверсификации инвестиций на величину риска, с которым столкнется инвестор при формировании портфеля из акций А и В.

.

Таким образом, при любых погодных условиях диверсификация инвестиций обеспечит инвестору доходность в размере 15 % в год. Исключение риска обусловлено характером изменения доходности двух активов. При увеличении доходности одного актива доходность другого актива снижается до отрицательных значений. Это говорит о том, что доходность рассматриваемых активов находится в обратной корреляционной зависимости.

Вернемся вновь к коэффициенту корреляционной зависимости, который, как отмечалось выше, выражает меру тесноты связи совместного движения двух переменных. Если при увеличении доходности одного актива доходность другого актива также растет, то говорят, что зависимость между этими переменными прямая, и коэффициент корреляции имеет положительное значение. Если же при изменении доходности одного актива доходность другого актива не изменяется, то коэффициент корреляции равен нулю, и говорят, что между доходностями этих активов нет связи. Если же при увеличении доходности одного актива доходность другого актива снижается, то говорят, что зависимость между доходностями таких активов обратная, и коэффициент корреляции меньше нуля.

Рассмотренный пример позволяет сделать вывод о том, что при обратной корреляционной связи между доходностями акций двух компаний можно полностью исключить риск, если инвестировать свои денежные средства в покупку акций этих двух компаний. На практике такие связи встречаются не очень часто. Обычно доходности акций большинства компаний находится в прямой зависимости, и коэффициент корреляции этой зависимости имеет положительное значение. Это обусловлено тем, что уровень доходности большинства акций, обращающихся на рынке ценных бумаг, зависит от состояния экономики в целом. Поэтому диверсификация инвестиций путем покупки двух таких активов не исключает полностью риск, но может снизить уровень риска.

Пример 6.4. Инвестор может вложить свои денежные средства в покупку акций компаний Дельта и Гамма. Ожидаемая норма доходности инвестиций, вложенных в акции компании Дельта 25 % в год, в акции компании Гамма -15 % в год. Уровень риска вложений средств в акции компании Дельта равен 20 %, в акции компании Гамма – 14 %. Предположим, что инвестор решил вложить 40 % своих средств в акции компании Дельта и 60 % средств – в покупку акций компании Гамма. Коэффициент корреляции равен +0,3. Определить доходность портфеля и уровень риска портфельного инвестирования.

Ожидаемую доходность портфеля определим по формуле 6.8.

= 0,4 × 20 + 0,6 × 15 = 17 % в год.

Уровень риска инвестиций, вложенных в акции двух компаний, находим из выражения 6.12.

= 13,2 %.

Полученные результаты показывают, что диверсификация инвестиций в принятом соотношении позволяет получить ожидаемую норму доходности инвестиций, равной 17 % в год при одновременном снижении уровня риска для портфеля в целом до 13,2 %.

Пример 6.5. Инвестор вложил все свои денежные средства в покупку акций компании Пирамида, то есть портфель сформирован из акций одной компании. Ожидаемая норма доходности этих акций равна 22 % и уровень риска – 20 %. А теперь предположим, что инвестор решил диверсифицировать свой портфель. С этой целью он продал половину акций компании Пирамида, и вырученные средства вложил в покупку акций компании Конус, которые имеют ту же цену, тот же риск (20 %) и ту же ожидаемую норму доходности (22 %). Коэффициент корреляции, определяющий тесноту зависимости ожидаемой доходности обеих компаний, равен 0,3. В этом случае ожидаемая норма доходности нового портфеля, сформированного из акций компаний Пирамида и Конус, составит (определяется из уравнения 6.8):

= 0,5 × 22 + 0,5 × 22 = 22 %.

Расчеты показывают, что диверсификация не принесла прироста нормы доходности инвестированного капитала. Однако диверсификации вложений капитала может оказать влияние на уровень риска инвестиций в целом, что видно из следующего расчета (на основе уравнения 6.9):

= 16,1 %.

Полученный результат свидетельствует, что реструктуризация портфеля позволила снизить уровень риска инвестиций с 20 до 16,1%, что является привлекательным для инвестора.

Теперь предположим, что инвестор вложил денежные средства поровну в покупку акций компаний Пирамида и Конус, причем акции обеих компаний имеют одинаковые показатели ожидаемой нормы доходности (22 %) и стандартного отклонения нормы доходности (20 %). Если нормы доходности этих акций имеют корреляционную связь, выражающейся коэффициентом корреляции, равной (+1), то реструктурированный портфель имеет такую же ожидаемую норму доходности, что и портфель, который сформирован только из акций компании Пирамида. Поэтому реструктуризация портфеля за счет покупки акций компании Конус не отразится ни на значении ожидаемой нормы доходности портфеля (22 %), ни на величине риска портфеля (20 %).

О чем говорит показатель коэффициента корреляции, равной +1? Это означает, что если ожидаемая норма доходности акций компании Пирамида снизится с 22 до 10 % в год, то для акций компании Конус этот показатель также должен снизиться с 22 до 10 % в год. Или, наоборот: при увеличении ожидаемой нормы доходности акций компании Конус с 22 до 30 % в год, ожидаемая норма доходности акций компании Пирамида должна также возрасти с 22 до 30 % в год. Практически, ожидаемые нормы доходности акций двух разных компаний никогда не будут совершенно коррелированными, и наиболее вероятно, что коэффициент корреляции для доходности этих акций будет больше нуля, но меньше единицы.

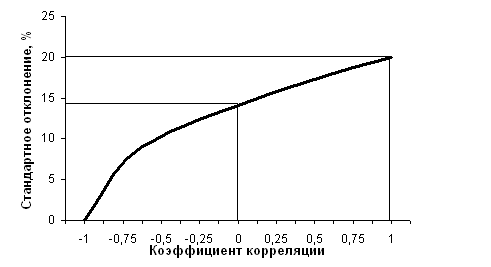
Отметим, что степень влияния диверсификации на уровень риска зависит от величины коэффициента корреляции: чем меньше значение этого коэффициента, тем ниже будет уровень риска для портфеля, включающего эти акции. Из уравнения 6.9 следует, что для рассмотренного примера при коэффициенте корреляции, равном (-1), риск портфеля акций будет равен нулю (рис. 6.4).

Рис. 6.4. Зависимость стандартного отклонения доходности портфеля из

двух активов от коэффициента корреляции [α₁ = σ₂ / ( σ₁ σ₂ )]

При нулевой корреляции стандартное отклонение доходности портфеля, в который включены два актива с σ₁ = σ_2, снижается с σ₁ = 20 % до 14,1 % ( ). При коэффициенте корреляции, равном +1, показатель риска портфеля будет иметь максимальное значение – 20 %. При таком уровне корреляционной зависимости диверсификация инвестиций не снижает риска портфеля в целом. Это гипотетический случай, поскольку на практике нормы доходности двух акций не имеют такую тесную корреляционную зависимость.

Рассмотрим зависимость дисперсии портфеля от коэффициента корреляции. В случае, когда значение коэффициента равно +1 (полная положительная корреляция доходности активов), то показатель дисперсии принимает вид:

(6.10)

Из формулы 6.10 видно, что при рассмотренном коэффициенте корреляции стандартное отклонение доходности портфеля, включающих два актива, равно средневзвешенному стандартному отклонению доходностей этих активов и увеличения доходности портфеля при включении таких активов в портфель не происходит. В этом случае наблюдается усреднение рисков вложений в отдельные активы.

Когда коэффициент корреляции равен –1 (полная отрицательная корреляция), то дисперсия будет иметь вид:

. (6.11)

Поскольку α₂ = 1 – α_1, то величину доли α₁ (при известных значениях σ₁, σ₂) можно подобрать так, чтобы стандартное отклонение доходности портфеля стало равным нулю:

α₁ = σ₂ / ( σ₁ + σ₂ ) (6.12)

Если подставить 6.10 в уравнение 6.9 (с учетом α₂ = 1 – α₁), то получим:

,

что и требовалось доказать.

Рис. 6.5. Доходность двух активов, включенных в портфель ( = -1)

Из двух активов с полной отрицательной корреляцией доходности всегда можно составить безрисковый портфель. Доходность такого портфеля в зависимости от времени не изменяется. На рис. 6.5 показатель доходности портфеля представлен в виде горизонтальной линии (R_port=17,5 %).

Две другие линии показывают возможные изменения доходностей активов, входящих в портфель. Падение доходности одного актива всегда полностью компенсируется ростом доходности другого актива.

При формировании портфеля инвестор всегда должен отбирать те активы, для которых коэффициент корреляции будет иметь минимальное значение. Такой портфель может обеспечить более высокий уровень ожидаемой доходности при том же риске по сравнению с другими портфелями.