6.2. Методы измерения риска

«Труднее всего отобрать именно то,

чего делать не следует».

Питер Ф. Драккер

При принятии финансовых решений возникает необходимость иметь объективные данные о степени риска, который может возникнуть при реализации такого решения. Единица измерения риска должна быть независимой от психологических особенностей индивидуума и его восприятия риска.

В основе измерения риска лежит распределение вероятностей исхода событий, которое описывает вероятность будущего изменения величины переменного фактора. Распределение вероятностей возможных значений переменного фактора может иметь дискретный или непрерывный характер. При принятии финансовых решений в качестве меры риска широко используется показатель среднеквадратичного отклонения (или дисперсии).

Пример 6.1. Предположим, что инвестор решил вложить свои свободные денежные средства в ценные бумаги. На рынке ценных бумаг его внимание привлекли акции компаний Лямбда и Сигма. Текущая цена этих акций равняется 100 руб. каждая, и дивиденды по ним не выплачиваются. Инвестор планирует купленные сегодня акции продать через год по более высокой цене и получить от своей операции доход, величина которого будет зависеть только от рыночной цены акции в день ее продажи. Поэтому инвестор должен иметь оценочные данные о цене акций каждой компании через год.

При расчете ожидаемой цены продажи используем концепцию дискретного распределения вероятностей и примем, что цена акций может изменяться в определенных пределах:

цена акции компании «Лямбда» - от 80 до 160 руб.;

цена акции компании «Сигма» – от 60 до 180 руб.

Для определения вероятности продажи акций в пределах указанных цен инвестор изучил данные по сделкам купли-продажи указанных акций за прошлый период и получил следующие результаты (табл. 6.1):

Таблица 6.1

Вероятность продажи акций по ценам от 60 до 180 руб.

Акции компании	Цена акции, руб.
	60	80	100	120	140	160	180
Лямбда	-	0,1	0,2	0,4	0,2	0,1	-
Сигма	0,1	0,1	0,2	0,2	0,2	0,1	0,1

Инвестор предполагает, что вероятность продажи акций по указанным ценам можно принять и на сделки с этими акциями в будущем году, то есть вероятность продажи акции компании Лямбда по цене 80 руб. равна 10 %, по цене 100 руб. – 20 % и т. д. Вероятность продажи акции компании Сигма по цене 60 руб. – 10 %, по цене 80 руб. – 10 % и т. д.

По полученным данным определим два показателя, которые позволят нам определить, акции какой компании более привлекательны для инвестора: ожидаемую цену акции и среднеквадратичное отклонение цены акции. Ожидаемая цена акции определяется из выражения:

, (6.1)

где Ц_i - i – ая цена акции, руб.; p_i - вероятность продажи акции по i – ой цене, доли ед.

Ожидаемая цена акции компании Лямбда равна:

Ц_Л = 80 × 0,1 + 100 × 0,2 + 120 × 0,4 + 140 × 0,2 + 160 × 0,1 = 120 руб.

Ожидаемая доходность сделки по купле и продажи акции компании Лямбда r через год равна:

r = (120 – 100) / 100 = 0,2 или 20 % в год.

Ожидаемая цена акции компании Сигма (Ц) будет равна:

Ц_С =60 × 0,1 + 80 × 0,1 + 100 × 0,2 + 120 × 0,2 + 140 × 0,2 + 160 × 0,1 + 180 × 0,1 = 120 руб.

Ожидаемая доходность сделки по купле и продажи акции компании Сигма r через год равна:

r = (120 – 100) / 100 = 0,2 или 20 % в год.

Таким образом, ожидаемая доходность акций обеих компаний одинакова, и инвестор не имеет четкой информации о предпочтительности вложений своих денежных средств в покупку акций определенной компании.

Среднеквадратичное отклонение вероятностей распределения цены акции σ выражает дисперсию цены акции. Этот показатель выражает меру достоверности ожидаемой цены акции и поэтому может служить в качестве меры риска или показателя неопределенности изменения цены акции. Среднеквадратичное отклонение вероятностей распределения цены акции определяется из выражения:

. (6.2)

Подставив значения цен акций и вероятность их наступления, определим значения среднеквадратичного отклонения цен по акциям рассматриваемых компаний:

для акций компании Лямбда:

= = 21,9 руб.

для акций компании Сигма:

= = 34,6 руб.

Полученные результаты показывают уровень неопределенности будущей цены акций. Для большинства видов распределения вероятностей существует незначительный шанс выхода фактической цены акции в будущем за пределы Ц ± 2σ.

Инвестор, сравнивая значения σ для акций рассматриваемых компаний, сделает свой выбор в пользу акций компании Лямбда, поскольку эти акции обладают меньшим уровнем риска (21,9) в сравнении с акциями компании Сигма, которые характеризуются большим уровнем риска (34,6) при одинаковой доходности акций этих компаний.

Иногда мерой риска может служить отношение среднеквадратичнго отклонения к ожидаемой цене акции. Для акций компаний Лямбда и Сигма оно равны 0,18 (21,9 / 120) и 0,29 (34,6 / 120). Эти показатели показывают, насколько ожидаемая цена акции реально близка к будущей фактической цене акции.

Выше рассмотренный пример иллюстрирует неопределенность цены акции в будущем. Эта неопределенность непосредственно транслируется и на величину дохода, который хочет получить инвестор, и на ставку доходности инвестированного капитала (табл. 6.2).

Таблица 6.2

Распределение вероятностей ставки доходности акций компании Лямбда

Будущая цена акции, руб.	80	100	120	140	160
Ставка доходности, %	-20	0	20	40	60
Вероятность	0,1	0,2	0,4	0,2	0,1

Ставка доходности при будущей цене акции, равной 80 руб.:

r = (80 - 100) / 100 = - 0,2 или -20 %.

Ставка доходности при будущей цене акции, равной 100 руб.:

r = (100 - 100) / 100 = 0.

Распределение вероятностей ожидаемой нормы доходности акций компании Лямбда представлено на рис. 6,2.

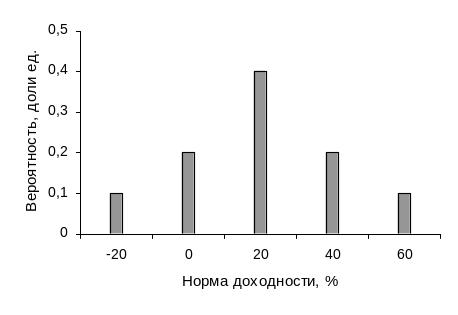
Рис.6.2. Дискретное распределение вероятностей ожидаемой

нормы доходности акций компании Лямбда

Аналогично рассчитываются ставки доходности для всех будущих цен акций компании Сигма (табл. 6.3).

Таблица 6.3

Распределение вероятностей ставки доходности акций компании Сигма

Будущая цена акции, руб.	60	80	100	120	140	160	180
Норма доходности, %	-40	-20	0	20	40	60	80
Вероятность	0,1	0,1	0,2	0,2	0,2	0,1	0,1

На основе данных табл. 6.2 и 6.3 определим ожидаемую доходность инвестиций, вложенных в акции компаний Лямбда и Сигма, а также значения среднеквадратичного отклонения доходности от ожидаемой ставки доходности инвестированного капитала.

Для расчета величины ожидаемой нормы доходности и стандартного отклонения доходности формулы 6.1 и 6.2 перепишем в виде:

, (6.3)

(6.4)

где r_k – доходность k – го актива, %; p_k – вероятность получения дохода по k – му активу, доли. ед.

По формуле 6.3 находим ожидаемую норму доходности при вложении денежных средств в покупку акций двух компаний:

r_expЛ = (-20) × 0,1 + 0 × 0,2 + 20 × 0,4 + 40 × 0,2 + 60 × 0,1 = 20 %;

r_expС = (-40)×0,1 + (-20)×0,1 + 0×0,2 + 20×0,2 + 40×0,2 + 60×0,1 + 80×0,1= 20 %.

Значения среднеквадратичного отклонения доходности от ожидаемой ставки доходности инвестированного капитала определим по формуле 6.4. Расчеты показывают, что для акций компании Лямбда величина σ = 21,9 %, а для акций компании Сигма значение σ = 34,6 %.

При рассмотрении влияния уровня риска на ожидаемую норму доходности акции следует иметь в виду множество значений, которые может принять данный показатель. В нашем примере ожидаемая цена акции компании Лямбда изменялись от 80 до 160 руб. с интервалом 20 руб. Предположим, что цена акции может меняться с интервалом 0,5 руб., тогда можно получить 160 возможных значений будущей цены акции ((160 - 80) / 0,5), и, следовательно, 160 значений ставки доходности по этой акции. Если по акции в будущем будут выплачиваться дивиденды, величина которых неопределенна, то в этом случае возможные значения ставки доходности по акции значительно возрастут, и тогда можно говорить о непрерывном распределении ожидаемой нормы доходности акций компании Лямбда.

При непрерывном распределении вероятность получения отдельного значения нормы доходности, например, 10 %, равно нулю. В этом случае мы измеряем вероятность получении любой доходности как площадь под кривой. Например, на рис. 6.3 вероятность получения нормы доходности между 15 и 25 % равна 0,4 (заштрихованная область под кривой между 15 и 25 % значениями нормы доходности акции). Если обратиться к рис. 6.2, то имеем ту же вероятность для получения нормы доходности, равной 20 %, при дискретном распределении вероятностей.

Рис. 6.3. Непрерывное распределение вероятностей ожидаемой

нормы доходности акций компании Лямбда

Легко сравнивать риски, когда ожидаемые доходности всех вариантов равны. А как выбирать вариант инвестиций из двух инвестиционных проектов, если они различаются и по ожидаемым нормам доходности и по рискам?

Рассмотрим два варианта инвестиций:

а) ожидаемая норма доходности актива А 15 % в год, стандартное отклонение 9 %;

б) ожидаемая норма доходности актива В 30 % в год, стандартное отклонение 15 %.

Какой из этих вариантов предпочтительнее?

Можно сказать, что второй вариант более рискован, поскольку значение стандартного отклонения для этого варианта больше в сравнении с первым вариантом. Однако такой ответ может привести к ошибочному выбору инвестиционного проекта. Обычно в таких случаях риск принято измерять относительной мерой, называемой коэффициентом дисперсии, или коэффициентом вариации. Величина этого показателя определяется как отношение стандартного отклонения ожидаемой нормы доходности актива к его ожидаемой норме доходности. В первом варианте его величина будет равна 9/15=0,6 или 60 %; во втором – 15/30=0,5 или 50 %. Второй вариант относительно менее рискован, несмотря на то, что само по себе стандартное отклонение доходности здесь выше.

Портфель, формируемый инвестором, состоит из нескольких активов, каждый из которых обладает своей ожидаемой доходностью. Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него активов. Ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него активов. Однако в отличие от ожидаемой доходности портфеля его риск не обязательно является средневзвешенной величиной стандачртных отклонений доходностей активов. Дело в том, что различные активы могут по-разному реагировать на изменение конъюнктуры рынка. В результате стандартные отклонения доходности различных активов в ряде случаев будут гасить друг друга, что приведет к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении изменяются доходности входящих в него активов при изменении конъюнктуры рынка и в какой степени.

Для определения степени взаимосвязи и направления изменения доходностей двух активов используют такие показатели как ковариация и коэффициент корреляции.

Показатель ковариации доходности активов А и В определяется по формуле:

, (6.6)

где: – средняя доходность активов А и В за n периодов; - доходность активов А и В в i-м периоде; n – число периодов, за которые регистрировалась доходность активов А и В.

Положительное значение ковариации говорит о том, что доходности активов изменяются в одном направлении, отрицательное – в обратном. Нулевое значение ковариации означает, что взаимосвязь между доходностями активов отсутствует.

Другим показателем, определяющим степень взаимосвязи изменения доходностей двух активов, служит коэффициент корреляции, который рассчитывается по формуле:

, (6.7)

где Сov_A,B – ковариация доходности активов А и В; σ_A, σ_B – стандартные отклонения доходности активов А и B.

Коэффициент корреляции изменяется в пределах от -1 до +1. Коэффициент корреляции – это статистическая мера степени линейной зависимости между двумя случайными переменными. При нулевой корреляции переменные x и y никак не связаны, то есть значения переменной y меняются совершенно случайно, вне зависимости от изменения значений переменной x. При приближении абсолютной величины коэффициента корреляции к единице зависимость между переменными приобретает все более определенный, линейный характер.

Среднеквадратичное отклонение, выражающее меру риска, обладает четырьмя важными свойствами:

1. На величину среднеквадратичного отклонения влияет только разность между ожидаемой ценой акции и разными ценами на акции, по которым могут быть реализованы эти акции. Если акция имеет только одну цену продажи, например, 150 руб., то говорят, что вероятность продажи акции по этой цене равна 1,0. В этом случае ожидаемая цена продажи также равна 150 руб. и среднеквадратичное отклонение цены акции будет равна нулю, поскольку колебание цены равно нулю. Следовательно, если для инвестиционного решения риск равен нулю, то показатель меры риска σ равен нулю.

2. При расчете показателя σ разность между вероятностной ценной и ожидаемой ценой продажи возводилась во вторую степень. В этом случае те ожидаемые цены, которые более удалены от ожидаемой цены акции, оказывают большее влияние на величину σ, чем те значения цен, которые незначительно отличаются от ожидаемой цены акции. Следовательно, при использовании в качестве меры риска среднеквадратичное отклонение цены акции следует иметь в виду то, что значительные разницы между ожидаемой ценой акции и будущими ценами на акции обусловливают больший риск.

3. Чем меньше вероятность продажи акции по какой-то цене, тем меньшее влияние оказывает эта цена на величину риска.

4. Среднеквадратичное отклонение цены акции измеряется в тех же единицах, что и ожидаемая цена акции, то есть в денежном выражении, например, в рублях, евро, долларах США и др.