Биномиальная модель Кокса-Росса-Рубинштейна

На рис. 29.2 представлено полное дерево цен акции при использовании биномиальной модели, которая была предложена Коксом, Россом и Рубинштейном. В нулевой момент времени цена акции равна S. В момент времени t мы имеем два значения цены акции – S × u и S × d; в момент времени 2t существует три возможных значений цены акции – S × u², S, S × d², и так далее. В общем случае, в момент времени it рассматриваются i+1 значений цены акции. То есть цена актива в каждом узле биномиального дерева равна:

S × u^j × d ^i-j j = 0, 1 ..., I . (29.23)

Отметим, что зависимость u = l/d используется при вычислении цены акции в каждом узле дерева на рис. 29.2. Например, S × u² × d = Su. Обратим также внимание на то, что движение по дереву, начинающееся с увеличения и заканчивающееся снижением стоимости приводят к той же величине стоимости, что и движение по дереву, начинающееся с уменьшения и заканчивающееся ростом стоимости. Это значительно сокращает число узлов на биномиальном дереве.

Оценка опционов начинается с конца дерева (с момента времени Т) и происходит в обратном порядке. В момент времени Т стоимость опциона известна. Например, стоимость опциона пут равна max (X – S_T, 0) и опциона колл - max(S_T - X, 0), где S_T – цена базисной акции в момент Т, а X – страйк цена опциона. Так как мы сделали предположение о безрисковом мире, значение стоимости в каждом узле в момент времени Т - t может быть рассчитана как ожидаемая стоимость в момент времени Т, дисконтированная по показателю r для момента времени t. Точно так же стоимость в каждом узле древа во время Т - 2t может быть рассчитана как ожидаемая стоимость во время Т - t, дисконтированная по r на момент времени t и т.д. Если опцион американский, необходимо проверять в каждом узле: выгодно ли для держателя опциона раннее его исполнение или предпочтительнее держать опцион в следующем отрезке времени t. В конечном счете, работая в обратном направлении, можно получить значение стоимости опциона в нулевой отметке.

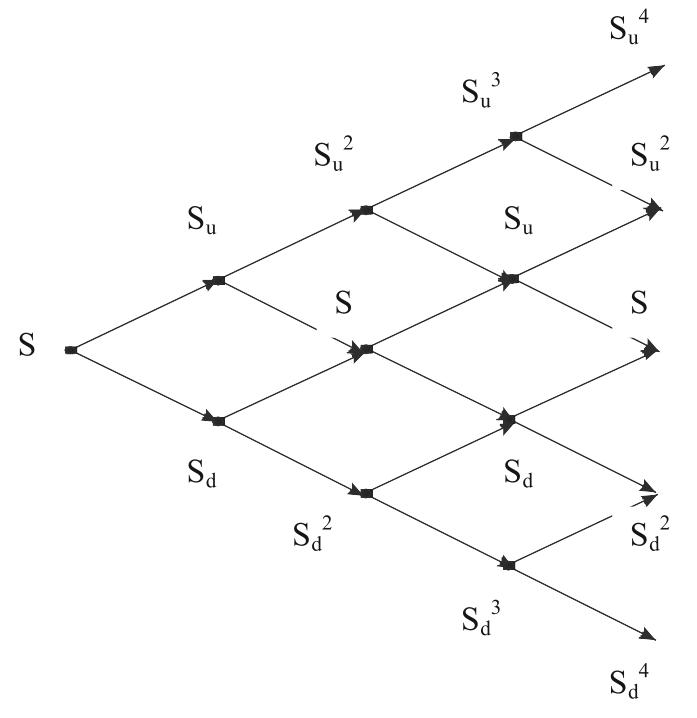
Рис. 29.2. Дерево, используемое для подсчетов цен опционов, в основе которых лежат акции

Пример 29.3. Рассмотрим американский опцион пут, в основе которого лежат акции без выплаты дивидендов, со сроком исполнения 6 месяцев. Цена базисной акции 100 долл., страйк цена опциона 95 долл., безрисковая процентная ставка 8% в год, и волатильность 30% в год. Определим цену опциона с помощью биномиального дерева, разделив интервал времени на 5. Исходным данным дадим следующие обозначения: S =100, X = 95, T= 0,5, r = 0,08, σ = 0,3, n = 5.

Определяем интервал времени Δt: Δt = 0,5/5 = 0,1года.

Затем находим значения u, d и p:

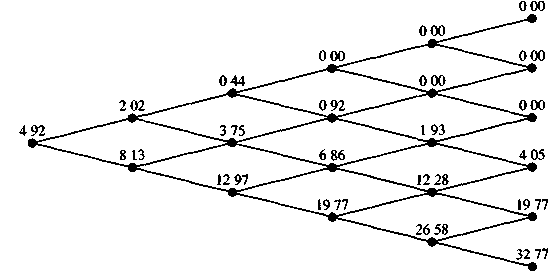
На рис. 29.3 показаны биномиальные деревья, отражающие изменение цены базисного актива (рис. 29.3а) и изменение цены американского опциона пут (рис.29.3б) по данным примера 29.1. Цена акции в j – ом узле (j = 0, 1,..., i) в период времени it рассчитывается как S×u^j×d^(i-j).

M

К

Е

а)

E

Е

б)

M

б)

К

Рис. 29.3. Биномиальное дерево для американского опциона пут, в основе которого лежат бездивидендные акции

Например, цена акции в узле М (i = 4, j = 1) – 100 × 1,0995 × 0,9095³ = 82,72 долл. (рис.29.3а). Стоимость опциона в конечных узлах рассчитана, как max (X – S_T, 0). Например, стоимость опциона в узле К равна: 95,00 – 75,23 = 19,77. (рис. 29.3б). Стоимости опциона в предпоследних узлах дерева рассчитаны на основе его цены в конечных узлах. Прежде всего, мы исходим из предположения, что реализация опциона в узлах дерева не осуществляется. Это означает, что стоимость опциона рассчитывается как приведенная стоимость ожидаемой цены опциона в момент времени t. Например, в узле E стоимость опциона рассчитана как:

(0,5186 × 0 + 4,05 × 0,4814) × e^-0,08×0,5 = 1,93 долл.

Аналогично рассчитана стоимость опциона в каждом узле дерева, то есть расчет цены опциона в узлах дерева с использованием метода обратной индукции. Итоговая цена американского опциона пут может быть найдена из условия:

(29.24)

Более удобно анализировать биноминальное дерево, когда в его узлах одновременно указываются цена базового актива и цена опциона.

Пример 29.4. Необходимо определить цену американского опциона пут при следующих заданных параметрах: текущая цена бездивидендной акции равна 50 евро, страйк цена 50 евро, безрисковая ставка 10 % в год, волатильность цены базовой акции 40 %, срок исполнения опциона 5 месяцев. Таким образом, запишем заданные параметры в следующем виде: S = X = 50, r = 0,1, T = 0,4167, σ = 0,4.

Разделим период обращения опциона на 5 интервалов продолжительностью по одному месяцу: Δt = 0,4167/5 = 0,0833 года.

На рис. 29.4 показано соответствующее биномиальное дерево оценки американского опциона пут. В каждом узле приводится два числа. Верхнее - показывает цену акции; нижнее – значение стоимости опциона.

Определим значения u, d и p:

Вероятность возрастания цены базисного актива равна 0,5076, вероятность убывания цены базисной акции 0,4924.

Цена базисной акции в j-м узле (j = 0, 1,..., i) в период времени it определяется как S×u^j×d^(i-j). Например, цена акции в узле A (i = 4, j = 1) равна

S_A = 50×1,1224×0,8909³ = 39,69 евро.

Стоимость опциона в конечных узлах определена как max (X – S_T , 0). Например, стоимость опциона в узле G равна: 95 – 75,23 = 19,77 евро.

G

Рис. 29.4. Биномиальное дерево для американского опциона пут, в основе которого лежат бездивидендные акции

Стоимости опциона в предпоследних узлах дерева рассчитаны на основе стоимостей в конечных узлах. Прежде всего, мы исходим из предположения, что реализация опциона в узлах дерева не осуществляется. Это означает, что стоимость опциона рассчитывается как приведенная стоимость ожидаемой цены опциона в момент времени t. Например, в узле E стоимость рассчитана как:

(0,5076 × 0 + 5,45 × 0,4924) e^{-0,10 × 0,0833} = 2,66 евро.

В узле А стоимость опциона пут равна

(0,5076 × 5,45 + 0,4924 × 14,64) e^{-0,10 × 0,0833} = 9,9 евро.

После этого необходимо проверить насколько целесообразно досрочное исполнение опциона. Досрочное исполнение опциона в узле Е пройдет по нулевой стоимости, поскольку в этом узле цена базисной акции и страйк цена опциона соответственно равны 50 евро. В этом случае предпочтительнее подождать и исполнить опцион ближе к моменту наступления срока его исполнения. В узле А ситуация будет иной. Если опцион будет реализован, его стоимость достигнет 50 – 39,69 = 10,31 евро. Это больше чем 9,9 евро. Если мы дошли до узла А, опцион необходимо реализовывать, и стоимость его будет 10,31 евро.

Цены опционов в более ранних узлах рассчитываются аналогичным способом. Обратите внимание, что не всегда лучше исполнять опцион на ранних стадиях, когда он «в деньгах». Рассмотрим узел B. Если опцион исполняется на ранней стадии, то его стоимость составляет 50 – 39,69 = 10,31 евро. Однако, если его удерживать, стоимость опциона может достигнуть

(0,5076 × 6,37 + 0,4924 × 14,64) × e^{-0,10 × 0,0833} = 10,35 евро.

Полученный результат позволяет сделать вывод, что в данном узле опцион пут реализовывать нет смысла, поскольку действительная его стоимость, соответствующая этому узлу, будет 10,35 евро, и инвестор потеряет на каждой акции 0,04 евро.

Продвигаясь по дереву в обратном порядке, определяется стоимость опциона в начальном узле, которая должна равняться 4,48 евро. Это значение мы получили численной оценкой текущей стоимости опциона. На практике необходимо учитывать, что интервал t должен быть гораздо меньше, а количество узлов – больше, чем в теоретической модели, которую мы рассматриваем. Действительное значение стоимости опциона пут, которое получается при бесконечно маленьком t, равно 4,29 евро.

Оценка индексных, валютных и фьючерсных опционов

Метод биномиального дерева можно также применять и для определения стоимости американских опционов колл и пут, в основе которых лежат акции, обеспечивающие периодические платежи по дивидендам при ставке q. Так как дивиденды обеспечивают возврат q, цена акции должна для безрисковой ситуации обеспечивать доходность r - q. Следовательно, уравнение (29.1) сводится к виду:

.

Следовательно, (29.18) преобразуется в

.

Уравнения (29.19) - (29.21) остаются в силе с учетом того, что

. (29.25)

В соответствии с вышесказанным численная процедура с использованием биноминального дерева для оценки американского опциона может использоваться, как и прежде, но с новым значением a.

Напомним читателю, что выше, при анализе индексных, валютных и фьючерсных опционов, мы рассматривали базисные активы в таких опционах как акции, по которым выплачивается постоянный дивидендный доход. В случае биржевого индекса, уместной дивидендной доходностью можно принять доходность портфеля с акциями, которые включаются для расчета индексного показателя. В случае валютного опциона – принимается иностранная безрисковая процентная ставка; в случае фьючерсного опциона в качестве дивидендной доходности выступает внутренняя безрисковая процентная ставка. С учетом этих принятых положений численный метод с использованием биномиального дерева может использоваться для оценки не только опционов на основе бездивидендных акций, но и индексных, валютных и фьючерсных опционов. Это мы покажем ниже на примерах.

Пример 29.5. Рассмотрим 4-месячный опцион колл американского стиля, в основе которого лежит индексный фьючерс при следующих исходных параметрах: текущая цена фьючерса 300 индексных пунктов, страйк цена опциона 300 индексных пунктов, безрисковая процентная ставка 8 % в год, волатильность индекса 40 % в год. Мы делим срок обращения опциона на четыре одномесячных периода с целью построения дерева. При принятой нами системе обозначений можем записать:

F = 300, X = 300, r = 0,08,  = 0,4, Т = 0,3333 и t = 0,0833.

Поскольку фьючерсный контракт аналогичен по свойствам акции, по которой выплачиваются дивиденды по постоянной ставке r, то в уравнении (29.25) q должен быть приравнен к r, что даст a = l.

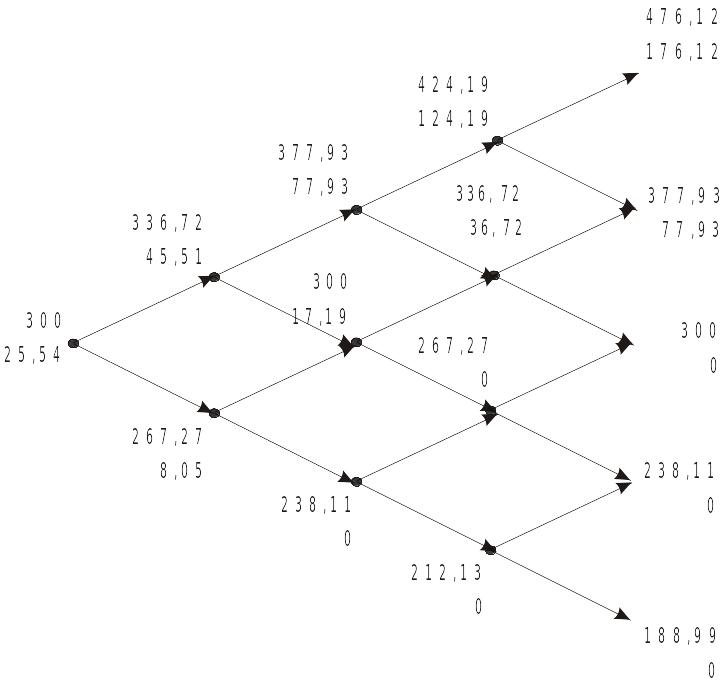
Рис. 29.5. Биномиальное дерево для оценки американского опциона колл, в основе которого лежит индексный фьючерс

Другие параметры, необходимые для построения дерева, будут иметь значения:

.

Цена базисной акции в j – ом узле (j = 0, 1,..., i) в период времени it определяется как S×u^j×d^(i-j). Стоимость опциона в конечных узлах определена как max (F_T – X, 0).

Биномиальное дерево с ценами индексного фьючерса и опциона колл показано на рис. 29.5. (Верхнее число - фьючерсная цена; нижнее – цена опциона). Полученная стоимость опциона 25,54 индексных пунктов.

Методику оценки американского валютного опциона пут с использованием биномиальной модели рассмотрим на следующем примере.

Пример 29.6. Рассмотрим американский опцион пут, в основе которого лежит обменный курс британского фунта стерлингов, со сроком обращения один год. Текущий валютный курс британского фунта равен 1,61 долл., страйк цена опциона 1,6 долл., безрисковая процентная ставка для условий США принята равной 8% в год, безрисковая процентная ставка для условий Великобритании равна 10% в год, волатильность обменного курса фунта стерлингов составляет 12% в год. Таким образом, заданные параметры можно записать в следующем виде: S =1,61, X =1,6, r = 0,08, r_f = 0,1,  = 0,12, и Т = 1. Мы делим срок обращения опциона на четыре 3–х месячных периода с целью построения дерева так, чтобы t = 0,25. В этом случае q = r_f, и на основе уравнения (29.25) значение а равно:

.

После нахождения величины а, переходим к определению других параметров, которые необходимы для построения модели биномиального дерева, отражающего изменения обменного курса и цены опциона пут.

.

Полученные значения искомых параметров позволяют построить биномиальное дерево, отражающее изменение цены опциона.

Биномиальное дерево, позволяющее проследить изменение обменного курса и цены опциона пут, показано на рис. 29.6. Для каждого угла дерева представлены две цифры: верхнее число - валютный курс; нижнее – цена опциона. Как показывают расчеты с использованием полученного дерева, цена американского валютного опциона пут с параметрами, которые заданы условиям задачи 29.6, равна 0,0782 долл.

Биномиальная модель дает возможность оценить и европейские опционы колл и пут. Кроме того, такая модель позволяет определить цену любой производной ценной бумаги, как американского стиля, так и европейского стиля.

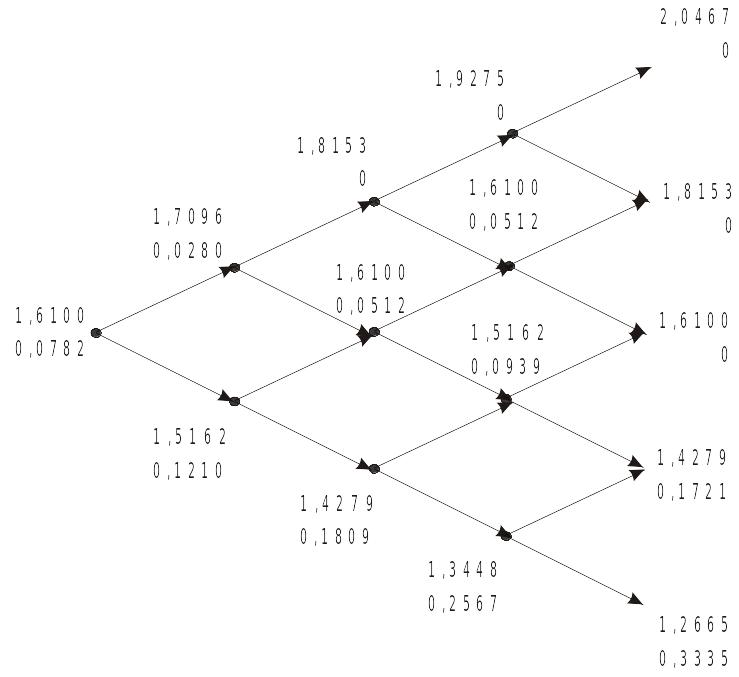
Рис. 29.6. Биномиальная модель для оценки американского опциона пут, в основе которого лежит обменный курс британского фунта

Резюме