Метод аппроксимации Бьерксунда и Стенсланда

В 1993 г. Бьерксунд и Стенсланд (Bjerksund and Stensland) для оценки американского опциона, в основе которого могут лежать акции, фьючерсы и валюта, предложили использовать метод аппроксимации. Этот аналитический метод можно наиболее эффективно использовать при компьютерном расчете цены опциона. Он базируется на выборе стратегии исполнения опциона, соответствующей цене близкой к I (триггерная цена).

Стоимость американского опциона колл по методу аппроксимации определяется по формуле:

, (29.7)

где (29.8)

(29.9)

Функция  (S, T, , H, I) задается в виде:

(29.10)

где (29.11)

(29.12)

(29.13)

Триггерная цена I определяется из выражения:

(29.14)

где ; (29.15)

и . (29.16)

Если то это условие является оптимальным для немедленного исполнения опциона и стоимость опциона должна равняться его внутренней стоимости (S – X). При условии досрочное исполнение опциона американского стиля будет невыгодным для владельца. В этом случае опцион должен исполняться по наступлению срока исполнения, и для определения стоимости такого опциона должна использоваться обобщенная модель Блэка-Шоулза.

Стоимость американского опциона пут может быть найдена путем преобразования стоимости опциона колл в пут следующим образом:

где С() – стоимость американского опциона колл с безрисковой процентной ставкой (r - b) и со смещением (– b).

Пример 29.2. Опцион колл американского стиля, в основе которого лежат акции компании «Глубахов и сыновья», имеет страйк цену 40 евро и срок исполнения 9 месяцев. Текущая цена базисной акции равна 42 евро, безрисковая процентная ставка 4 % в год, дивидендный доход принят 8 % в год, волатильность равна 35 % в год. Следовательно, исходные параметры для расчета цены американского опциона колл методом Бьерксунда и Стенсланда можно представить следующим образом:

S = 42, X = 40, T = 0,75, r = 0,04, b = 0,04 – 0,08 = - 0,04,  = 0,35.

Прежде всего, по формуле (29.9) находим значение :

.

На втором этапе расчетом по формуле (29.16) определяем значения В_ и В₀:

;

На следующем этапе определяем значение h(T):

.

Триггерную цену находим из выражения (29.14):

Затем по формуле (29.8) находим значение :

Подставив полученные значения в формулу (29.7), находим стоимость американского опциона колл:

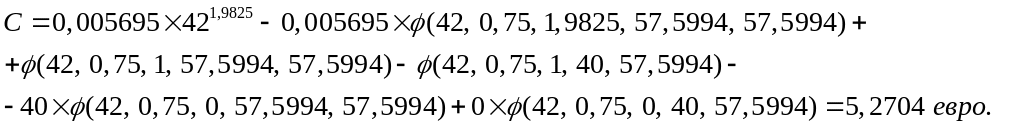Значения функций  в формуле (29.7) определяется на основе (29.10).

Для сравнения была подсчитана цена европейского опциона колл с аналогичными исходными параметрами. Расчеты показали, что стоимость такого европейского опциона колл равна 5,0975 евро за акцию.

29.2. Численные методы

Как магнит мощно притягивает к себе железо,

так серебро и золото, которые человек дарит,

притягивают к нему сердца людей.

Гийом де Лоррис

Биномиальная модель

Численные методы для оценки опционов или других производных ценных бумаг более гибки в сравнении с аналитическими методами оценки опционов и поэтому могут эффективно использоваться для определения цен для многих видов опционов. При оценке опциона численным методом исходят из предположения, что в основе опциона лежит один вид актива. Это позволяет строить биномиальное дерево цен опциона.

Рассмотрим метод оценки опциона, в основе которого лежат бездивидендные акции. Разделим жизненный цикл ценной бумаги на большое количество интервалов t. Предположим, что в каждом из интервалов цена базисной акции перемещается от ее начального значения S к одному из двух новых значений, Su и Sd. Эта модель проиллюстрирована на рис. 29.1. В общем случае, u > 1 и d < 1. Предполагается, что переход от S до Su – это возрастание цены опциона, а переход от S до Sd – снижение цены опциона. Примем вероятность увеличения цены p, тогда вероятность убывания будет равной 1 - p.

р

1-р

Рис. 29.1 Изменения цены акции в промежутке времени t по биномиальной модели

Для оценки опциона (или любой другой производной ценной бумаги), можем предположить:

1. Ожидаемая доходность всех торгуемых ценных бумаг равна безрисковой процентной ставке.

2. Будущие денежные потоки могут быть оценены, дисконтируя их ожидаемые значения по безрисковой дисконтной ставке.

При использовании биномиальной модели используем принципы безрисковой оценки.

Параметры p, u, и d должны определять значения среднего и дисперсии цены акции в течение интервала времени t. Так как мы имеем дело с безрисковой ситуацией, ожидаемая доходность акции характеризуется безрисковой процентной ставкой r. На практике r выбирается как показатель доходности бескупонной облигации с тем же сроком жизни, что и опцион. Следовательно, ожидаемое значение цены акции в конце интервала времени t равна , где S – цена акции в начале интервала времени. Из этого следует, что

(29.17)

или

(29.18)

Дисперсия изменения цены акции на небольшом интервале времени t соответствует . Так как дисперсия переменной Q определяется как , где E обозначает ожидаемое значение стоимости, то из этого следует:

или

(29.19)

Уравнения (29.18) и (29.19) налагают два условия на p, u, и d. Третье условие, которое обычно используется – следующее:

u = 1/d.

Можно легко показать, что три условия – это:

p = (a – d)/(u – d) , (29.20)

, (29.21)

, (29.22)

где при условии, что очень мало.