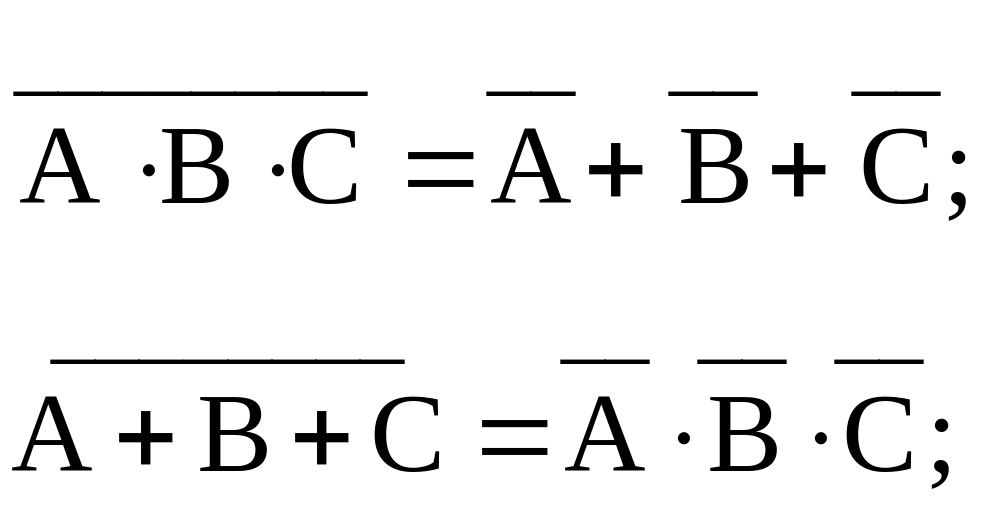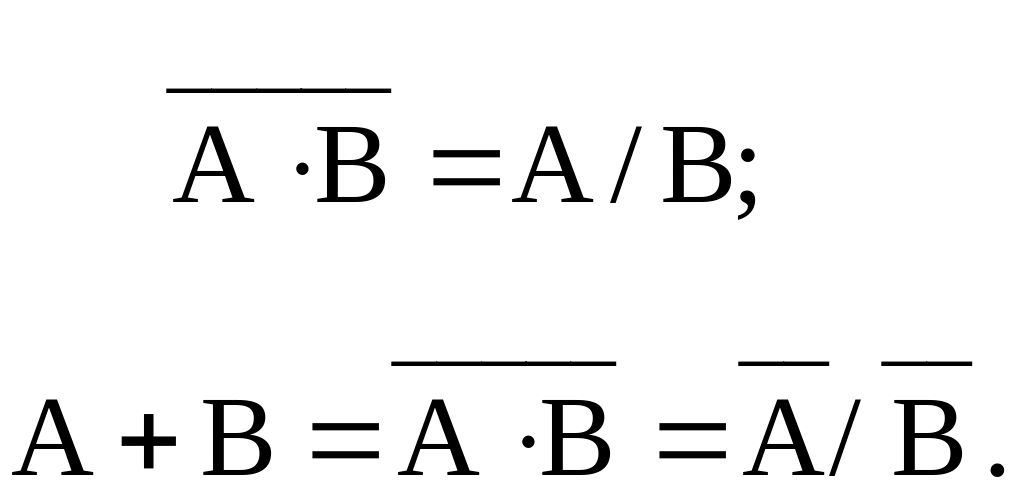Специфические аксиомы и теоремы алгебры логики.

Законы де Моргана
являются одной из иллюстраций свойства
двойственности и, как уже отмечалось,
могут быть сформулированы в виде:
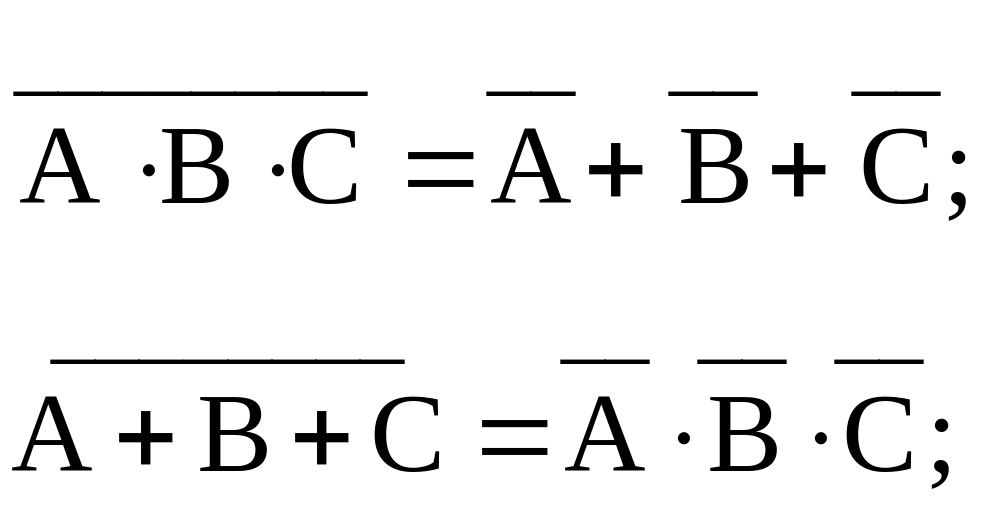
Из законов Моргана
следует, что, имеется возможность
выражать конъюнкцию через дизъюнкцию
и отрицание, или дизъюнкцию - через
конъюнкцию и отрицание. Законы де Моргана
и следствия из них справедливы для
любого количества переменных.
Функция
сложения по модулю 2
представляется следующим образом:
 .
.
Для этой функции
справедливы следующие аксиомы:
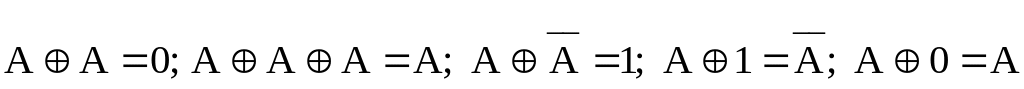 .
.
На основании
рассмотренных аксиом и свойств
элементарных логических функций можно,
например, вывести
правила представления функций
«И», «ИЛИ», «НЕ»
через функцию сложения по модулю 2 и
наоборот:
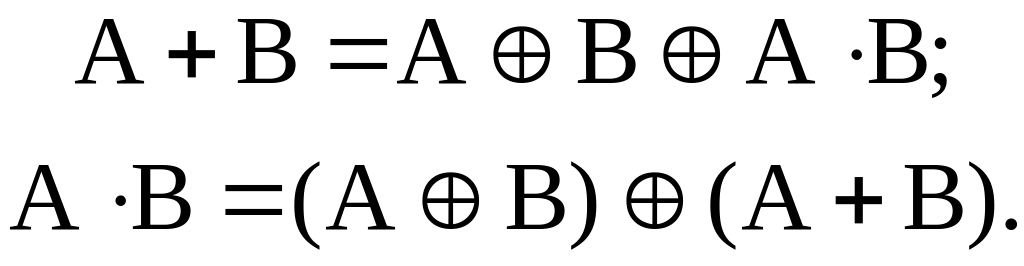
Функции
«И»,
«ИЛИ», «НЕ»
через функцию Шеффера выражаются
следующим образом:
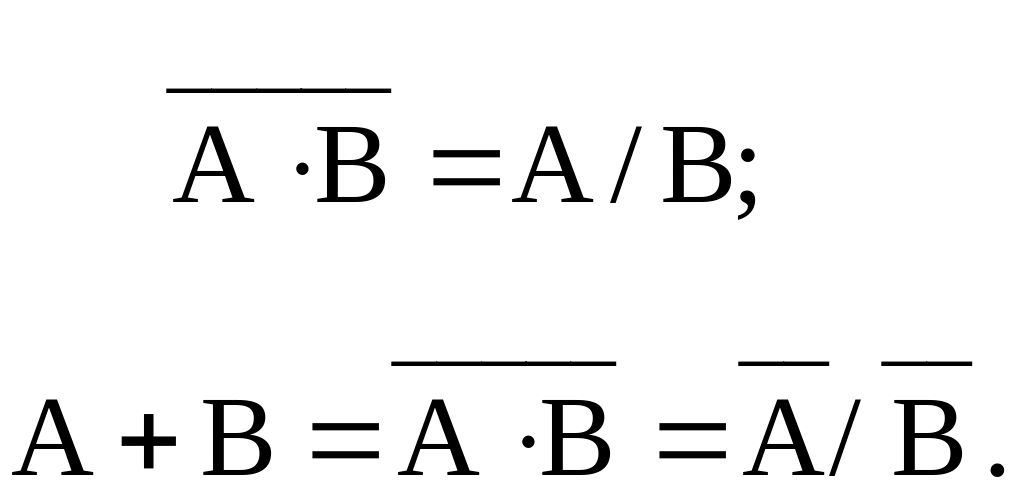
Функция Пирса
может описываться следующими выражениями:
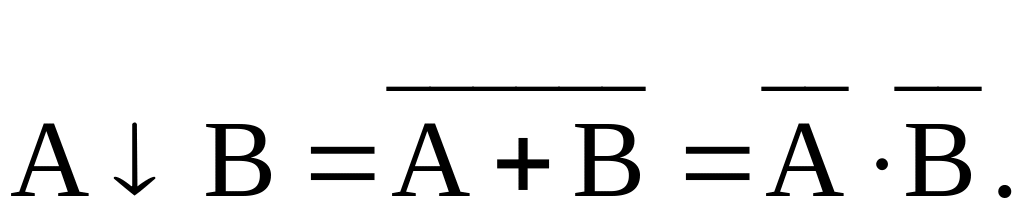
Для этой функции
справедливы следующие аксиомы:
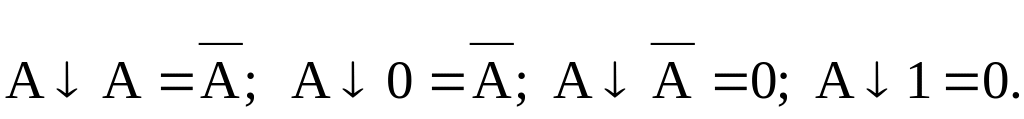
Функции
«И»,
«ИЛИ», «НЕ»
выражаются через функцию Пирса следующим
образом:
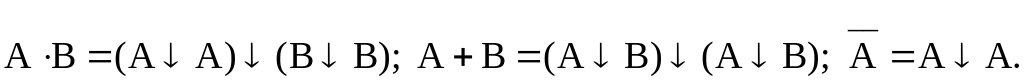
Следует отметить,
что логические выражения, содержащие
операции дизъюнкции и конъюнкции, можно
преобразовывать (раскрывать скобки,
выносить общий множитель, переставлять
местами члены и т.д.) по правилам алгебры,
считая формально дизъюнкцию операцией
сложения, а конъюнкцию - операцией
умножения. В
алгебре логики, в отличие от обыкновенной
алгебры, знак + либо знак
означают
логическую связку
«ИЛИ»,
а знак умножения "•" либо знаки
и &, означают логическую связку
«И».
Булево
выражение
представляет собой формулу, состоящую
из логических констант и логических
переменных, соединенных знаками
логических операций.
18