Уравнение трех моментов (уравнения Клапейрона)

- изгибающие моменты на левой, средней правой опорах двух соседних пролетов;

- длины левого и правого соседних пролетов;

- площади грузовых эпюр моментов под левым и правым пролетом соответственно;

- расстояние от центра тяжести до левой границы левого пролета;

- расстояние от центра тяжести до правой границы правого пролета.

Глава 12. Устойчивость сжатых стержней. §58. Устойчивость упругого равновесия. Критическая сила.

В системе, находящейся в деформированном состоянии, равновесие между внешними нагрузками и внутренними силами упругости может быть устойчивым, безразличным, неустойчивым.

Центрально приложенная сила, превышение которой вызывает потерю устойчивости первоначальной формы равновесия тела, называется критической силой.

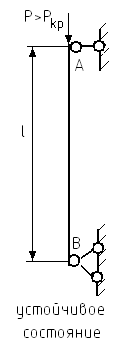
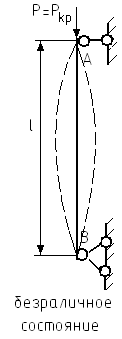
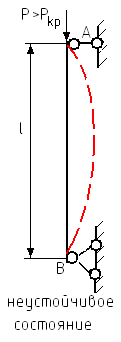
Неустойчивая форма равновесия связана с неограниченным ростом деформаций и напряжений.

Поэтому неустойчивое положение ведет к разрушению.

Для обеспечения определенного запаса устойчивости необходимо выполнение следующего условия:

Р – действующая нагрузка.

- коэффициент запаса устойчивости.

Продольным изгибом называется изгиб стержня, связанный с потерей устойчивости прямолинейной формы равновесия стержня. При потере устойчивости прогиб произойдет к оси наименьшей жесткости.

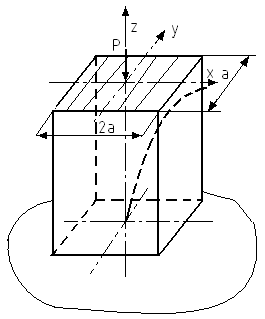
- ось х – ось наименьшей жесткости.

Прогиб произойдет перпендикулярно оси х (на нас).

Р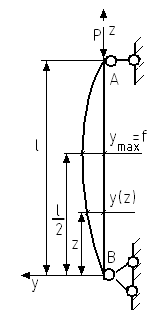 ассмотрим прямой стержень длиной l постоянного сечения с шарнирно закрепленными концами А и В.

М омент отрицателен, т.к. если мы развернем АВ по часовой стрелке на 90⁰, сжатое волокно окажется снизу.

Введем обозначение:

Формула Эйлера

- эйлерова сила.

Данная формула показывает, что стержень изгибается по синусоиде.

Значение В характеризуется величиной максимального прогиба.

Возьмем производную: :

п – число полуволн синусоиды, умещающихся по длине изогнутого стержня.

Чем выше п, тем напряженное состояние стержня более опасно.

§59. Влияние условия закрепления концов стержня на величину критической силы.

1. Центрально сжатый стержень, жестко закрепленный снизу.

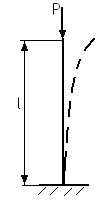
2. Центрально сжимаемый стержень, закрепленный по концам.

3. Жестко закрепленный центрально сжимаемый стержень.

4. Центрально сжимаемый стержень с подвижным верхним и неподвижным нижним концом.

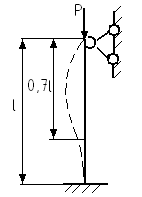
μ – коэффициент приведения длины. Он показывает, чему равна длина одной полуволны синусоиды при заданной длине стержня.

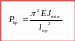- приведенная длина стержня;

l – реальная длина стержня.