
- •Перший модуль. Тема 1. Елементи канторівської теорії множин Діаграми Ейлера — Венна.
- •Підмножини. Потужність множини
- •2. Перша схема дослідження бінарного відношення.
- •3. Відношення еквівалентності. Класи еквівалентності
- •3.6. Фактормножина за відношенням еквівалентності.
- •Екстремальні елементи множин.
- •Композиція та обернення відображень
- •Композиція відображень
- •Тема 2 . Елементи математичної логіки Рівносильність. Бульові функції та їх властивості.
- •Булеві функції двох перемінних
- •Представлення булевих функцій за допомогою дднф
- •Перемикальні схеми Базові логічні елементи в електроніці
- •2.5.1. Потенціальні елементи позитивної і негативної логіки
- •2.5.2. Принцип дії напівпровідникових логічних елементів
- •Числення висловлювань
- •Числення педикантів
- •Предикати. Формули логіки предикатів
- •Квантори
- •Другий модуль. Тема 3 Теорія графів
- •Способи задання графів. Степені вершин
- •Матриці суміжності графа
- •Цикломатичне число
- •Хроматичне число
- •Множина внутрішньої стійкості
- •Множина зовнішньої стійкості
- •Теорема Шеннона
- •Радіус і діаметр графа
- •Ядро графа
- •Ізоморфізм графів
- •Маршрути у графі. Зв'язність графів
- •8. Аналіз та модифікації алгоритмів пошуку
- •Транспортні сітки
- •Тема 1. Елементи канторівської теорії множин 1
- •Тема 2 . Елементи математичної логіки 14
- •Тема 3 Теорія графів 26
Перемикальні схеми Базові логічні елементи в електроніці
![]() Февраль
27th, 2012
Февраль
27th, 2012 ![]() admin
admin
В цифровій електроніці використовуються елементи які володіють певними характеристиками та типом роботи. Для того, щоб вони працювали потрібно вибудувати спеціальний логічний ланцюжок, який дозволить об’єднати їх в спеціальну структуру яка б діяла за певними правилами не порушуючи їх та виконуючи поставлені перед нею завдання. Ці елементи мають спеціальну логіку за допомогою якої складлаються в ще набагато складніші, які виконують ще важчі завдання.
Логічними елементами комп’ютерів є електронні схеми І, АБО, НЕ, І-НЕ, АБО-НЕ і інші. За допомогою цих схем можна реалізувати будь-яку логічну функцію, яка б заставила компоненти комп’ютера працювати.
Роботу логічних елементів описують за допомогою таблиць істинності. В цьому прикладі буде описано роботу елементів І, АБО, НЕ.
Схема «І» реалізує кон’юнкцію (логічне множення) двох або більш логічних значень. Одиниця на виході схеми «І» буде тоді і тільки тоді, коли на всіх входах будуть одиниці. Коли хоча б на одному вході буде нуль, на виході також буде нуль.
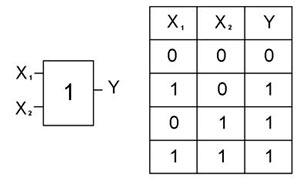
Операція кон’юнкції на функціональних схемах позначається знаком & (читається як «амперсэнд»), є скороченим записом англійського слова «and».
Схема «АБО» реалізовує диз’юнкцію (логічне складання) двох або більш логічних значень. Коли хоча б на одному вході схеми «АБО» буде одиниця, на її виході також буде одиниця. На схемі операція диз’юнкції позначається знаком «1».
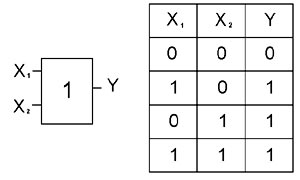
Схема (інвертування) не реалізує операцію заперечення. Якщо на вході схеми 0, то на виході 1. Коли на вході 1 на виході 0. Для того щоб побачити різницю між простою схемою і схемою заперечення слід подивитись на позначення її виходу. На початку виходу присутній притаманний їй кружечок.
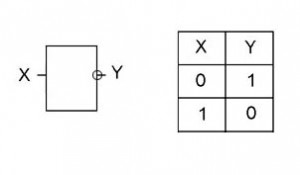
Технічні аналоги булевих функцій
2.5.1. Потенціальні елементи позитивної і негативної логіки
Перетворення інформації в цифрових системах здійснюється електронними пристроями двох класів: комбінаційними схемами (КС) і цифровими автоматами (ЦА). Докладніше КС і ЦА будуть розглянуті в розділі 3 і 4.
Логічні стани КС представляються двома рівнями напруги (потенціалу): високим Н (high), близьким до джерела живлення і низьким L (low). Існують два типи логіки: позитивна, коли високий потенціал кодує логічну одиницю (Н), а низький – логічний нуль (L). Негативна логіка навпаки : "1" – L ,"0" – Н.
Елемент, який виконує логічну функцію, можна оцінювати з позицій і позитивної, і негативної логіки. В обох випадках його функціональна роль буде різною, що видно із правил де Моргана.
Для кон’юнкції: ![]() .
Користуючись цим правилом на рисунку
2.5 приведена таблиця
і діаграма двоходової
схеми, що характеризує роботу схеми
І, а також таблиця
і діаграма для
схеми АБО.
Не важко замітити,
що ці дві пари повністю рівнозначні,
тобто схему І можна описати діаграмою
№8, а схему АБО діаграмою №14 (див.
рис.2.4).
.
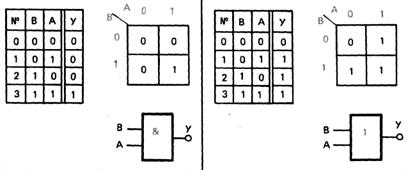
Користуючись цим правилом на рисунку
2.5 приведена таблиця
і діаграма двоходової
схеми, що характеризує роботу схеми
І, а також таблиця
і діаграма для
схеми АБО.
Не важко замітити,
що ці дві пари повністю рівнозначні,
тобто схему І можна описати діаграмою
№8, а схему АБО діаграмою №14 (див.
рис.2.4).
|
|
|
|
||
|
|
|
|
Рис.2.5 – Різні форми опису роботи схем І та АБО
Для функції І–НЕ
за законом де Моргана: ![]() ,
тобто маємо для негативної логіки
функцію НЕ–АБО.
,
тобто маємо для негативної логіки
функцію НЕ–АБО.
Отже, логічні елементи, що виконують логічні функції, можна зображувати у двох еквівалентних формах – позитивної і негативної логіки. Маючи зображення елемента, його еквівалентну форму можна отримати, якщо: а) в основному полі зображення елемента змінити символ операції (І на АБО чи навпаки); б) замінити на протилежні входи і виходи – прямі на інверсні і навпаки (рис.2.6).
Позитивна логіка більш поширена і тому в довідниках наводиться позитивна логіка.
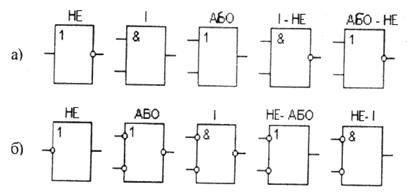
Рис.2.6. Умовне позначення логічних елементів
позитивної (а) і негативної (б) логіки
Якщо логічні елементи відповідно з’єднати, то можна реалізувати складні логічні функції. Сукупність різних типів елементів, достатніх для відтворення будь-якої складності логічної функції, називається логічним базисом.
Як відмічено раніше, набір функцій І, АБО, НЕ є функціонально повним, а елементи І та НЕ є базисом, бо з них можна реалізувати і функцію АБО за правилом де Моргана
![]() ,
,
як показано на рис.2.7.
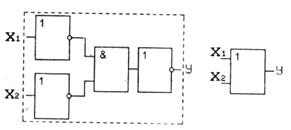
Рис.2.7. Схема утворення елемента АБО
З’єднання елементів І–НЕ дає змогу реалізувати логічні функції І, АБО, НЕ, як показано на рис.2.8. Універсальність елемента І–НЕ забезпечила йому широке застосування.
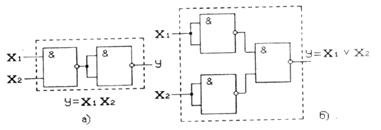
Рис.2.8. Схема реалізації в логічному базисі І–НЕ
функцій І (а) та АБО (б)
