Множина внутрішньої стійкості

Визначення: Множина SX графа G =<X, Г> називається внутрішньо стійкою, якщо ніякі дві вершини з S не суміжні, тобто для будь-якого xiS має місце Г(x_i)S = , т.е:

 xi S (Г(x_i)S = )

Множина внутрішньої стійкості, що містить найбільше число елементів, є найбільшою внутрішньо стійкою множиною, а число елементів цієї безлічі називається числом внутрішньої стійкості графа.

П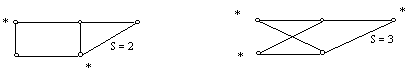 риклад: Два графи з різними числами внутрішньої стійкості

Рис. 1. Графи з числом внутрішньої стійкості два і три

Найменше число внутрішньої стійкості мають повні графи, максимальне число - нуль-графи.

П риклад: Числа внутрішньої стійкості повних і порожніх графів, що вмикають три і чотири вершини, відповідно рівні 1, 1, 3

Рис. 2. Числа внутрішньої стійкості повних і порожніх графів

Множина зовнішньої стійкості

Визначення: Множина T  X графа G = <X, Г> називається зовні стійкою, якщо будь-яка вершина, що не належить Т, з'єднана ребрами з вершинами з Т, тобто

 x_i  T (Г(x_i)T  )

Множина зовнішньої стійкості, що містить мінімальне число елементів, називається найменшою зовні стійкою множиною, а число його елементів називається числом зовнішньої стійкості графа G.

П риклад: Однакові числа зовнішньої стійкості для різних графів, що вмикають п'ять вершин, відповідно рівні 2, 2

Рис. 3. Графи з числом зовнішньої стійкості два

Найменше число зовнішньої стійкості - у повних графів Т = 1, у нуль-графа безліч зовнішньої стійкості включає усі вершини графа Т = n.

П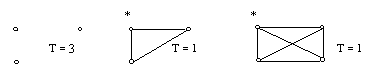 риклад: Числа зовнішньої стійкості порожнього і повних графів, що вмикають три і чотири вершини, відповідно рівні 3, 1, 1

Рис.4 . Числа зовнішньої стійкості порожнього і повного графів

Теорема Шеннона

Для кожних двух графів маємо:

,

Але якщо для графа G₁ існує відображення , таке, що множина внутрішньо стійка, то

Доведення:

Якщо S₁ i S₂ найбільш внутрішньо стійкі множини, то

Нехай відображення для графа G і множина внутрішньо стійка. Для будь-яких и

і

. Нехай S₀ –найбільша внутрішньо стійка множина графа .

Безпосередньо перевіряється, що також внутрішньо стійке і . Розподіляємо елементи із по k класам в залежності від елемента в парі . Кожен клас отримує не більше, ніж елементів. Отже,

.

Звідси і випливає доведена рівність.

Радіус і діаметр графа

Відстанню між вершинами v і w зв'язного графа (позначається d (v,w)) називається довжина найкоротшого простого ланцюга, що з'єднує вершини v і w.

Ексцентриситетом е(v) довільної вершини v зв'язного графа G = (V, Е) називається найбільша з відстаней між вершиною v і всіма іншими вершинами графа G, тобто е(v) = .

Діаметром зв'язного графа G (позначається D(G)) називається максимальний з усіх ексцентриситетів вершин графа G. Мінімальний з усіх ексцентриситетів вершин зв'язного графа G називається його радіусом і позначається R(G).

Вершина v називається центральною, якщо е(у) = R(G). Центром графа С називається множина всіх його центральних вершин.