
- •Перший модуль. Тема 1. Елементи канторівської теорії множин Діаграми Ейлера — Венна.
- •Підмножини. Потужність множини
- •2. Перша схема дослідження бінарного відношення.
- •3. Відношення еквівалентності. Класи еквівалентності
- •3.6. Фактормножина за відношенням еквівалентності.
- •Екстремальні елементи множин.
- •Композиція та обернення відображень
- •Композиція відображень
- •Тема 2 . Елементи математичної логіки Рівносильність. Бульові функції та їх властивості.
- •Булеві функції двох перемінних
- •Представлення булевих функцій за допомогою дднф
- •Перемикальні схеми Базові логічні елементи в електроніці
- •2.5.1. Потенціальні елементи позитивної і негативної логіки
- •2.5.2. Принцип дії напівпровідникових логічних елементів
- •Числення висловлювань
- •Числення педикантів
- •Предикати. Формули логіки предикатів
- •Квантори
- •Другий модуль. Тема 3 Теорія графів
- •Способи задання графів. Степені вершин
- •Матриці суміжності графа
- •Цикломатичне число
- •Хроматичне число
- •Множина внутрішньої стійкості
- •Множина зовнішньої стійкості
- •Теорема Шеннона
- •Радіус і діаметр графа
- •Ядро графа
- •Ізоморфізм графів
- •Маршрути у графі. Зв'язність графів
- •8. Аналіз та модифікації алгоритмів пошуку
- •Транспортні сітки
- •Тема 1. Елементи канторівської теорії множин 1
- •Тема 2 . Елементи математичної логіки 14
- •Тема 3 Теорія графів 26
Перший модуль. Тема 1. Елементи канторівської теорії множин Діаграми Ейлера — Венна.
У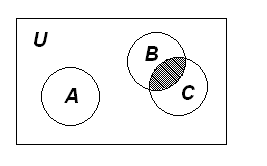 процесі вивчення множин і функцій
бувають корисними певні графічні
зображення. У випадку множин з цією
метою застосовують так звані діаграми
Ейлера
— Венна
(їх
часто називають діаграмами
Ейлера або
діаграмами
Венна). На
цих діаграмах схематично зображають
універсальну множину U
у
вигляді прямокутника, а різні підмножини
універсальної множини – у вигляді
кругів (або інших фігур, наприклад
трикутників).
процесі вивчення множин і функцій
бувають корисними певні графічні
зображення. У випадку множин з цією
метою застосовують так звані діаграми
Ейлера
— Венна
(їх
часто називають діаграмами
Ейлера або
діаграмами
Венна). На
цих діаграмах схематично зображають
універсальну множину U
у
вигляді прямокутника, а різні підмножини
універсальної множини – у вигляді
кругів (або інших фігур, наприклад
трикутників).
Е
Мал..1
Підмножини. Потужність множини
1. Поняття підмножини. Множина А називається підмножиною множини В, якщо кожний елемент множини А належить множині В. У такому випадку пишуть
А
![]() В або B
В або B![]() A
A
(читають: «Множина А є підмножиною множини В», або «Множина А є частиною множини В», або «Множина В містить множину A»).
Запис A![]() B
(або А
B
(або А![]() В)
означає, що
не всі елементи множини
А належать
множині В.
В)
означає, що
не всі елементи множини
А належать
множині В.
Множина А
називається
правильною
частиною множини
В, якщо А
В, але А
![]() В.
В.
Приклади:
1) N Z, Z Q, N R, Z+ N0;
{а, k} {а, f, k,
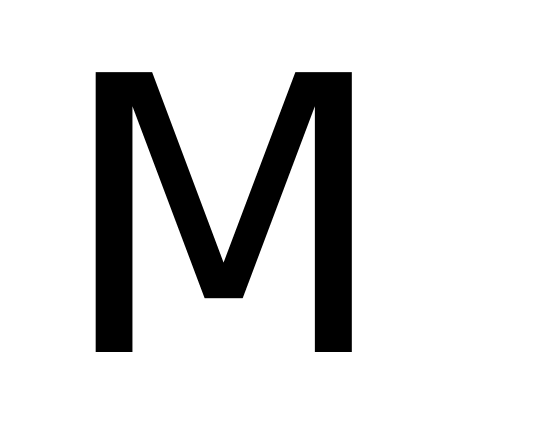 };
};{x
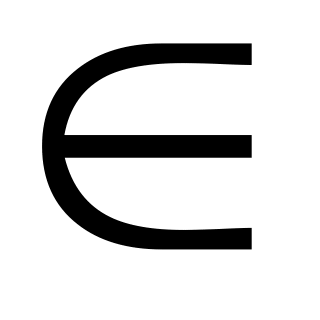 N
N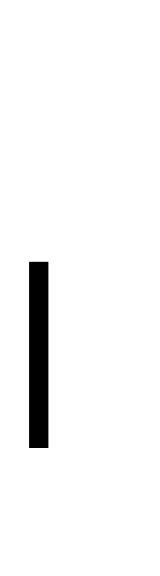 а
а
 х і
b
х)
{х
N
а
+ Ь
х),
де а, Ь
— фіксовані цілі числа;
х і
b
х)
{х
N
а
+ Ь
х),
де а, Ь
— фіксовані цілі числа;{0, 1, 2} {1, 2}, N N;
{1, {2}} {1, 2}.
У прикладах 1, 2 кожна з множин, що лежать зліва від знака (знак включення), є правильною частиною другої множини.
Щоб обгрунтувати включення А В, досить встановити:
коли а А, то а В, або
коли а В, то а А. Легко переконатися, що:
A A;
якщо A В, В С, то A С.
якщо A В, В A, то А = В.
Отже, для обгрунтування рівності А = В досить встановити, що множина A є підмножиною множини В, а В — підмножиною множини A (порівняйте § 1, п. 3).
Нехай А—довільна
фіксована множина. На основі першої
властивості A
A,
тобто довільна множина є своєю підмножиною.
Крім множини A,
яка є своєю підмножиною, існує
ще одна множина, яка є підмножиною
множини A
(і відрізняється
від A,
якщо А
![]() ).
Такою множиною
є порожня множина
.
Справді, якщо а
А, то а
.
Отже,
A.
).
Такою множиною
є порожня множина
.
Справді, якщо а
А, то а
.
Отже,
A.
Зауважимо, що в літературі знак іноді використовують лише для нерівних множин. У такому разі запис А В означає, що кожний елемент множини А належить множині В, але не всі елементи множини В належать множині А. Якщо ж множини А і В рівні, то використовують знак В такому разі A А, але А А.
Зауважимо також, що запис А В С далі означатиме: A В, В С.
2. Множина підмножин. Буліан. Разом з множиною А іноді доводиться розглядати множину всіх підмножин множини A, яку на честь Дж. Буля (Джордж Буль (1815— 1864) —англійський логік і математик) називають буліаном множини А і позначають так: B(А).
Отже, за означенням
B(A)={B B A}.
Зрозуміло, що B (А) містить як порожню множину , так і саму множину A Наприклад, якщо
A= (а, Ь,c),
то
B(A)={ , {a},{b}, {c}, {a,b}, {a,c}, {b,c}, A}.
{с}, {а, Ь), {а, с}, {Ь, с}, А}.
Очевидно, що коли В А, то В B(А) і навпаки. Аналогічно, якщо а А, то {а} А і {а} B(А).
З наведеного вище прикладу бачимо, що коли множина
A = {а, Ь, с)
містить 3 елементи,
то множина В(![]() )
містить уже 8 = 23
елементів.
Взагалі, якщо множина А
містить п
елементів, то
буліан B
(А) містить
2п
елементів.
Тому множину B
(А) часто
називають ще множиною-степенем
множини А
і позначають
так:
)
містить уже 8 = 23
елементів.
Взагалі, якщо множина А
містить п
елементів, то
буліан B
(А) містить
2п
елементів.
Тому множину B
(А) часто
називають ще множиною-степенем
множини А
і позначають
так:
![]() (A).
Така термінологія зберігається для
довільних, не
обов'язково скінченних, множин.
(A).
Така термінологія зберігається для
довільних, не
обов'язково скінченних, множин.
3. Універсальна
множина. Вивчаючи
те чи інше питання,
будуючи ту чи іншу математичну теорію,
розглядають
різні підмножини тієї або іншої конкретної
множини.
Наприклад, вивчаючи питання про
подільність чисел, розглядають
різні підмножини множини натуральних
(N) або цілих (![]() )
чисел: множини
чисел, що діляться на 3 або на
9; чисел, які в результаті ділення на
натуральне число т
мають одну і
ту саму остачу; множини простих чисел
тощо. Аналогічно,
вивчаючи рівняння або нерівності,
розглядають
різні підмножини множини дійсних (R)
або комплексних (С) чисел: область
визначення та область допустимих
значень; множини коренів рівняння чи
розв'язків нерівності
тощо. В геометрії теж доводиться
розглядати різні підмножини певних
множин: сукупності точок площини або
прямої; сукупності
прямокутних трикутників тощо.
)
чисел: множини
чисел, що діляться на 3 або на
9; чисел, які в результаті ділення на
натуральне число т
мають одну і
ту саму остачу; множини простих чисел
тощо. Аналогічно,
вивчаючи рівняння або нерівності,
розглядають
різні підмножини множини дійсних (R)
або комплексних (С) чисел: область
визначення та область допустимих
значень; множини коренів рівняння чи
розв'язків нерівності
тощо. В геометрії теж доводиться
розглядати різні підмножини певних
множин: сукупності точок площини або
прямої; сукупності
прямокутних трикутників тощо.
Множину, різні підмножини якої доводиться розглядати в процесі вивчення якогось питання, називають універсальною множиною і часто позначають буквою U (або буквою Т — від англійського слова Тоtаl).
Залежно від кола питань, що вивчаються, універсальною множиною може бути одна з числових множин (И, Z, Q, R, С). У геометрії універсальною множиною часто є площина або пряма.
4. Про рівнопотужні множини. Одними з основних досягнень канторівської теорії множин є поширення поняття "кількість елементів" зі скінченних множин на нескінченні та формулювання принципу, за яким можна порівнювати за "кількістю елементів" нескінченні множини. Зокрема, несподіваним та незвичайним виявився той факт, що різні нескінченні множини можуть мати різну "кількість елементів", тобто для нескінченностей також існує своя ієрархія.
Канторівська ідея грунтується на такому спостереженні: для того щоб порівняти за кількістю елементів дві скінченні множини, зовсім необов'язково перелічувати елементи кожної з них. Можна діяти таким чином. Наприклад, необхідно порівняти за кількістю дві множини - множину S студентів та множину M всіх місць в аудиторіях факультету. Запропонуємо кожному студенту зайняти одне місце. Якщо кожен студент отримає місце і при цьому в аудиторіях не залишиться жодного вільного місця, то очевидно, що кількість елементів в обох множинах S і M однакова. У противному разі, множина S містить більше елементів ніж множина M, або навпаки. Очевидно, що запропонована процедура встановлює деяку функціональну відповідність між множинами S і M. У першому випадку ця відповідність виявляється взаємно однозначною, в той час як у другому і третьому випадках умови взаємної однозначності не виконуються: або порушується умова повної визначеності (принаймні один студент не дістав місця), або порушується умова сюр’єктивності (хоча б одне місце залишилося вільним).
Принагідно зауважимо, що багато хто з математиків вважає, що описаний простий спосіб порівняння кількостей елементів у двох скінченних множинах логічно передує виникненню поняття числа.
Кількість елементів скінченної множини A прийнято позначати через |A|.
Таким чином, неважко переконатись, що між двома скінченними множинами A і B існує взаємно однозначна відповідність тоді і тільки тоді, коли |A|=|B|.
Сформульоване твердження дозволяє розв'язувати задачу обчислення кількості елементів множини A шляхом встановлення взаємно однозначної відповідності між множиною A і деякою множиною B, кількість елементів якої відома або легко може бути визначена. Для ілюстрації цього методу доведемо наступну важливу теорему про кількість підмножин заданої скінченної множини.
Теорема 1.1. Нехай A = {a1,a2,...,an} - скінченна множина з n елементів (|A|=n), тоді кількість усіх підмножин множини A дорівнює 2n, тобто 2|A|.
Доведення. Розглянемо множину всіх кортежів (b1,b2,...,bn) довжини n, які складаються з двійкових цифр 0 або 1 (тобто biB={0,1}, i=1,2,...,n). Очевидно, що множина цих кортежів є Bn.
Встановимо таку відповідність між підмножинами множини A і кортежами з Bn. Кожній підмножині A'A поставимо у відповідність двійковий кортеж (b1,b2,...,bn) такий, що
0, якщо aiA',
bi =
1, якщо aiA'.
За цим правилом порожній множині A відповідає кортеж (0,0,...,0), самій множині A - кортеж (1,1,...,1), а підмножині A' = {a2, a4 } - кортеж (0,1,0,1,0,...,0). Встановлена відповідність є взаємно однозначною. Отже кількість усіх підмножин множини A дорівнює |Bn |.
Методом математичної індукції доведемо, що |Bn| =2n.
Для n=1 маємо B1= B і |B| = 2 = 21.
Припустимо, що |Bk-1 | = 2k-1. З того, що кожному елементові (b1,b2,...,bk-1) множини Bk-1 відповідають два елементи (b1,b2,...,bk-1,0) і (b1,b2,...,bk-1,1) множини Bk випливає, що кількість елементів у множині Bk вдвічі більша від кількості елементів у множині Bk-1.
Тобто |Bk | =|Bk-1 |*2 =2k-1*2 = 2k. Теорема 1.1 доведена.
Множину всіх підмножин деякої множини A (скінченної або нескінченної) часто позначають через (A) і називають булеаном множини A. З доведеної теореми випливає, що для скінченної множини A виконується | (A)|= 2|A|.
Множини A і B назвемо рівнопотужними або множинами, які мають рівні (однакові) потужності, якщо існує взаємно однозначна відповідність між множинами A і B.
Відношення на множинах. Відношення порядку на множинах.
САМОСТІЙНЕ ВИВЧЕННЯ
1. Переріз відношення. Фактормножина.
2. Перша схема дослідження бінарного відношення.
3. Відношення еквівалентності. Класи еквівалентності
3.1. Рефлексивні та антирефлексивні відношення.
3.2. Симетричні і антисиметричні відношення.
3.3.Транзитивні відношення.
3.4.Відношення еквівалентності.
3.5. Класи еквівалентності.
3.6. Фактормножина за відношенням еквівалентності.
1.
Переріз відношення.
Фактормножина.
Нехай R
— відношення
від А до
В (тобто
R
А![]() В)і
а
А.
Позначимо
через Rа
сукупність
усіх таких елементів b
B,
для яких <a,
b>
R.
Визначена так множина Rа
називається
перерізом відношення R
по елементу а. Отже,
за означенням перерізу
В)і
а
А.
Позначимо
через Rа
сукупність
усіх таких елементів b
B,
для яких <a,
b>
R.
Визначена так множина Rа
називається
перерізом відношення R
по елементу а. Отже,
за означенням перерізу
Ra={b <a, b> R
Наприклад, якщо
R={<1, 2>, <2, 1>, <1, 3>, <2, 3>, <3, 4>},
А =
В = {1,
2, 3, 4}, то перерізом множини R
по елементу а=1(1
A)
є множина {2, 3}, оскільки <1, 2>
R
і (1, 3)![]() .
Отже, R1
= {2, 3}. Аналогічно:
.
Отже, R1
= {2, 3}. Аналогічно:
R2={1,3}, R3={4}, R4=
Сукупність усіх перерізів відношення R за елементами множини А називають фактором або фактормножиною множини В за відношенням R і позначають: В/R. Отже, за означенням
B\R={Ra a A}.
Так, у попередньому прикладі
В/R = {R1, R2, R3, R4},
або, що те саме,
В\R ={{2, 3}, {1, 3}, {4}, }.
Оскільки елементами буліана B (А) є підмножини множини А, довільна фактормножина В\R(R A В) є підмножиною буліана В (А): (В/R B (В).
Іноді елементи
множини А і
фактор-множини ВR
зручно
записувати у вигляді таблиці
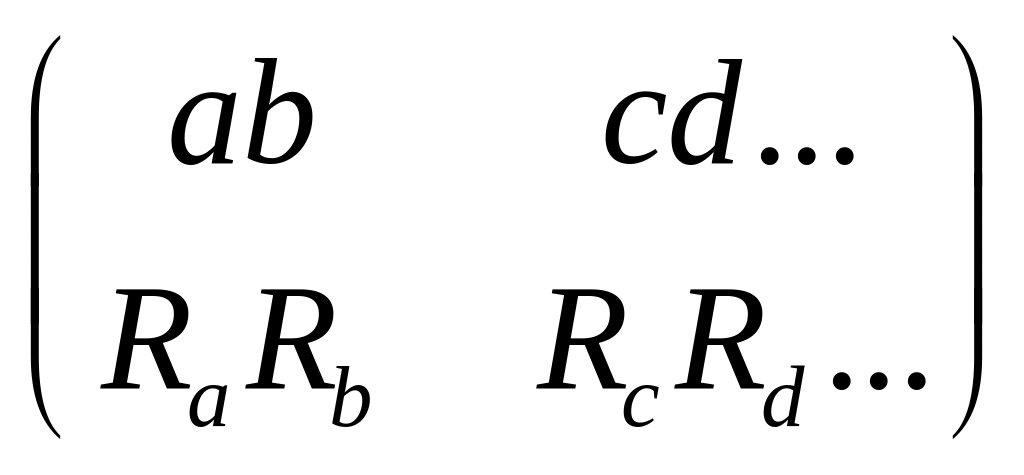
У першому рядку її записано елементи множини А у другому — елементи множини В/R. Попередній приклад можна записати у вигляді такої таблиці:
![]()
Зауважимо, що таблицю часто записують ще так:
А |
Ь |
c |
d |
… |
Ra |
Rb |
Rc |
Rd |
... |
Нехай R — відношення від А до В і A1—деяка підмножина множини А. Перерізом відношення R за множиною А1 називається об'єднання усіх перерізів відношення R за елементами множини А1:
RA=![]() Ra
Ra
Зокрема, якщо у попередньому прикладі покласти A1={2, 3}, то
RA
= R2![]() Rз={1.
3}
(4}={1, 3, 4}.
Rз={1.
3}
(4}={1, 3, 4}.
Аналогічно:
R{1,2} = R1 R2= {2, 3} {1, 3} = {1, 2, 3},
RA=R1 R2UR3 R4=B
Взагалі, якщо A = R_, то RA = R+, тобто переріз відношення R по лівій його області дорівнює правій області цього відношення (Rr_ = R+).
