Тема 10 термодинамический анализ процессов в компрессорах

Компрессор – это машина для повышения давления и перемещения газов и паров.

В компрессоре механическая энергия, подводимая к валу компрессора, преобразуется в кинетическую энергию потока и потенциальную энергию давления газа, при этом газ в процессе сжатия в компрессоре нагревается.

По принципу действия компрессоры делятся на объемные и динамические. Основными из объемных компрессоров являются поршневые и винтовые компрессоры; основными из динамических компрессоров являются центробежные и осевые компрессоры.

В объемных компрессорах изменение давления газа происходит за счет изменения объема рабочей камеры, в динамических компрессорах изменение давления газа происходит за счет взаимодействия движущегося с большими скоростями потока с элементами проточной части компрессора.

В объемных компрессорах газ в процессе сжатия обычно охлаждается и от него отводится теплота в окружающую среду, поэтому эти компрессоры называют также охлаждаемые компрессоры. В динамических компрессорах скорости движения газа в проточной части компрессора большие, теплообмена с окружающей средой практически не происходит, поэтому процесс сжатия газа в этих компрессорах принимается адиабатным, а компрессоры называют также неохлаждаемые (адиабатные) компрессоры.

Вопрос 1. Термодинамическая модель компрессора

С точки зрения термодинамики компрессор представляет собой открытую термодинамическую систему. В нем происходит стационарное течение потока газа.

Применим систему уравнений поточного процесса к компрессору.

1) Уравнение неразрывности (уравнение массового расхода)

, кг/с.

2) Уравнение I закона термодинамики для рассматриваемой системы

, Вт

Для компрессора можно пренебречь разностью кинетических энергий и потенциальных энергий положения потока во входном и выходном патрубках: и .

Тогда получим

.

В компрессоре мощность подводится из окружающей среды, т.е. работа совершается над системой, поэтому мощность, потребляемая компрессором .

Тогда получим

,

Откуда

- для охлаждаемых компрессоров;

- для неохлаждаемых компрессоров, т.к. Q_внеш=0.

Разделив полученные уравнения на массовый расход, получим удельную работу компрессора, т.е. работу, затрачиваемую на сжатие и перемещение 1кг рабочего тела:

, Дж/кг - для охлаждаемых компрессоров;

, Дж/кг - для неохлаждаемых компрессоров.

3) Закон сохранения механической энергии (для 1 кг), Дж/кг

или, учитывая, что и , получим

.

4) Уравнение II закона термодинамики (для 1кг), Дж/кг

- для охлаждаемых компрессоров;

- для неохлаждаемых компрессоров, т.к. q_внеш=0.

5) Уравнение состояния газа

или или

Вопрос 2. Охлаждаемые компрессоры.

2.1 Идеальный (совершенный) поршневой компрессор

Рассмотрим схему и принцип действия идеального одноступенчатого поршневого компрессора. (схема из Луканина).

Компрессор состоит из поршня 1, кривошипно-шатунного механизма 2, соединенного с приводом компрессора 3, и цилиндра 4, корпус которого охлаждается водой или воздухом. В крышке цилиндра размещены всасывающий 5 и нагнетательный 6 клапаны, которые открываются автоматически под действием перепада давлений.

Для исследования работы компрессора используется индикаторная диаграмма, которая является графическим представлением процесса изменения давления в цилиндре при перемещении поршня.

Принцип действия поршневого компрессора. При движении поршня слева направо давление в цилиндре становится меньше давления р₁, и под действием разности этих давлений открывается всасывающий клапан 5. Происходит процесс всасывания по линии 4-1 и цилиндр заполняется газом. При обратном движении поршня всасывающий клапан закрывается, и газ сжимается по линии 1-2. Давление в цилиндре увеличивается до тех пор, пока не станет больше давления р₂. Под действием разности этих давлений открывается нагнетательный клапан 6, и газ выталкивается поршнем в сеть потребителя по линии 2-3. Затем нагнетательный клапан закрывается, и все процессы повторяются.

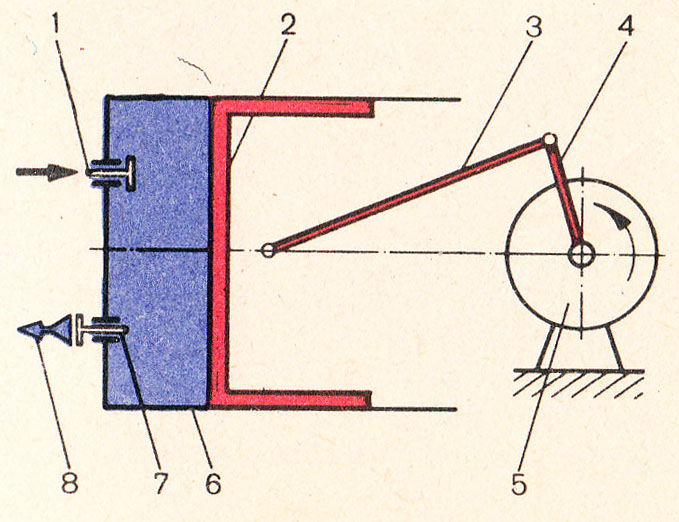
1— всасывающий клапан; 2 — поршень; 3 — шатун; 4— кривошип;

5 — электродвигатель; . 6 — цилиндр; 7 — нагнетательный клапан;

8 — сжатый газ.

Индикаторную диаграмму не следует смешивать с рv – диаграммой, которая строится для постоянного количества вещества. В индикаторной диаграмме линии всасывания 4-1 и нагнетания 2-3 не изображают термодинамические процессы, так как количество рабочего тела в этих процессах меняется, а его состояние остается постоянным.

Идеальный поршневой компрессор – это компрессор, в котором протекают равновесные процессы, отсутствует трение, поршень подходит к крышке цилиндра вплотную, без зазора, отсутствуют потери давления при проходе газа через клапаны, всасывание и нагнетание газа происходит при постоянных давлениях р₁ и р₂.

Основной задачей при термодинамическом расчете компрессора является определение удельной работы, затрачиваемой на сжатие газа.

Из закона сохранения механической энергии применительно к компрессору имеем

.

При =l_тр=0 (то есть для идеального компрессора) получим теоретическую работу компрессора, затрачиваемую что на сжатие и перемещение 1 кг газа

пл.4123.

Величина этой работы зависит от характера процесса сжатия. В идеальном поршневом компрессоре процесс сжатия газа, в зависимости от условий охлаждения цилиндра, можно производить по изотерме 1-2_Т, по изоэнтропе 1-2_S и по политропе 1-2 (при 1<n<k).

Сжатие по изотерме дает наименьшую затрачиваемую работу, т. е. наиболее энергетически выгодно. В этом случае из уравнения I закона термодинамики для охлаждаемых компрессоров имеем

.

Видно, что в изотермическом процессе нужно отводить от сжимаемого в компрессоре газа в виде теплоты всю затраченную на сжатие работу, что не реально. Чтобы приблизить процесс сжатия к изотермическому наружная поверхность цилиндра охлаждается водой или воздухом. При этом происходит политропный процесс с показателем политропы n = 1.18  1.2 (при k=1,4).

Из уравнения политропного процесса получим

.

Тогда удельная теоретическая работа компрессора, Дж/кг

.

Умножив на массовый расход газа , кг/с, получим теоретическую мощность, потребляемую компрессором

, Вт.

где - объемный расход газа на входе в компрессор, м³/с.