Контрольные вопросы

1. Как нужно складывать напряжения U_а и U_c? Почему?

2. Как получается треугольник сопротивлений?

3. Какие соотношения между сопротивлениями и углами этого треугольника применяют в расчетах электрических цепей?

4. Как выбирается масштаб тока и напряжения для построения векторной диаграммы?

ЛАБОРАТОРНАЯ РАБОТА № 30

Неразветвлённая цепь переменного тока с активным сопротивлением,

индуктивностью и ёмкостью. Резонанс напряжений

Цель работы: 1. Исследовать неразветвлённую электрическую цепь

переменного тока.

2. Построить векторные диаграммы токов и напряжений

для каждого режима работы.

В результате выполнения лабораторной работы студент должен:

знать: - основные законы электротехники

уметь: - собирать электрические цепи по схемам;

- производить измерения тока и напряжения при помощи мульти

метра;

- строить векторные диаграммы

Оборудование: лабораторный стенд.

Краткие теоретические сведения

Когда по цепи (рис. 30.1) с последовательным соединением конденсатора и ка­тушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсаторе Uc отстает от тока I на 90°, а напряжение на катушке индуктивности Ul опережает ток на 90°. Эти напряжения находятся в противофазе (повернуты относи­тельно друг друга на 180°).

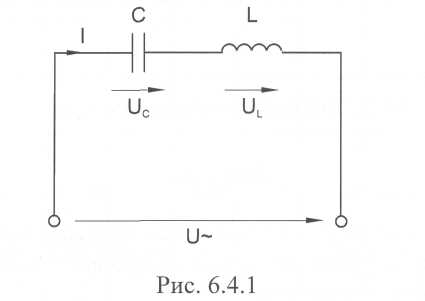
Рис. 30.1

Если одно из напряжений больше другого, цепь оказывается либо преимущест­венно индуктивной (рис. 30. 2), либо преимущественно емкостной (рис. 12.3). Если напряжения U_l и U_c имеют одинаковые значения и компенсируют друг друга, то сум­марное напряжение на участке цепи L - С оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и прово­дов. Такое явление называется резонансом напряжений (рис. 30.4).

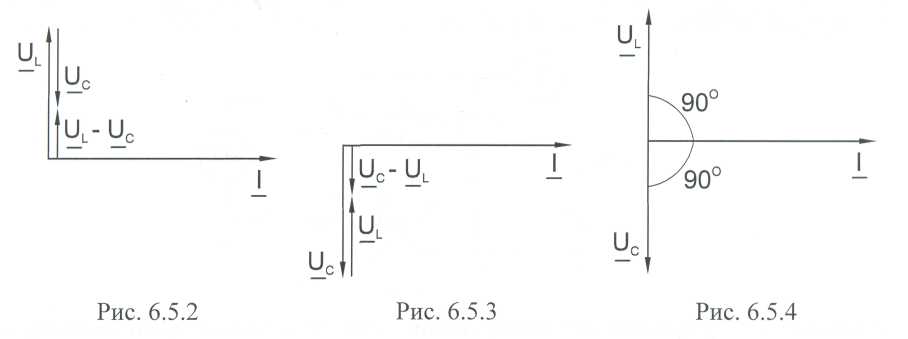
Рис. 30.2 Рис. 30.3 Рис. 30.4

При резонансе напряжений реактивное сопротивление цепи

X = X_L-X_C

оказывается равным нулю. При заданных значениях L и С резонанс может быть полу­чен путем изменения частоты.

Поскольку X_l = ωL, а Хс = 1 / ωС, то резонансная частота ω₀ может быть опре­делена из уравнения:

ω₀L - 1 / ω₀С = 0,

откуда

Полное сопротивление цепи при резонансе оказывается равным небольшому ак­тивному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U_l и U_c могут существенно (в десятки раз!) превышать прило­женное напряжение.

Порядок проведения работы

Задание

Для цепи с последовательным соединением конденсатора и катушки индуктив­ности измерьте действующие значения тока I и напряжений U, Uc, Ul при ω = ω₀, ω< ω₀ и ω> ω₀. Постройте векторные диаграммы.

Порядок выполнения работы

• Соберите цепь согласно схеме (рис. 30.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердеч­ника полоски бумаги в один слой (немагнитный зазор).

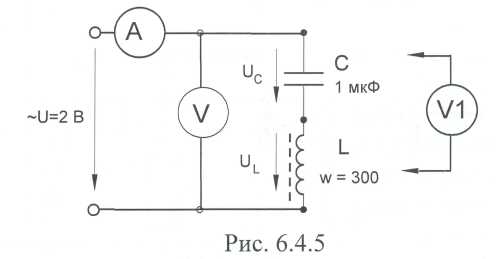
Рис. 30.5

• Изменяя частоту приложенного напряжения, добейтесь резонанса по максимально­му току.

• Произведите измерения и запишите в табл. 30.1 результаты измерений при резо­нансе f = fo, при f₁ = 0,75f₀ и f₂ = l,25f₀.

Таблица 30.1

	I, мА	U, в	UL,B	UC,B
f0 =
f1 =
f2 =

• Постройте в одинаковом масштабе векторные диаграммы на рис. 30.6 для каж­дого из рассмотренных случаев.

Рис. 30.6

Контрольные вопросы

1. В какой цепи может возникнуть резонанс напряжений и что для этого

необходимо?

2. Какая частота называется резонансной?

3. При каком условии напряжение на ёмкости в последовательной цепи с

параметрами R, L, С будет наибольшим?

ЛАБОРАТОРНАЯ РАБОТА № 31

Параллельное соединение резистора и конденсатора, резистора и катушки индуктивности

Цель работы: 1. Исследовать разветвлённые электрические цепи

переменного тока.

2. Построить векторные диаграммы токов и напряжений

для каждой исследуемой цепи.

В результате выполнения лабораторной работы студент должен:

знать: - основные законы электротехники

уметь: - собирать электрические цепи по схемам;

- производить измерения тока и напряжения при помощи мульти-

метра;

- производить измерения активной мощности при помощи ватт-

метра

- строить векторные диаграммы

Оборудование: лабораторный стенд.

Краткие теоретические сведения

Когда цепь (рис. 31.1) с параллельным соединением резистора и конденсатора (а) или резистора и катушки индуктивности (б) включена на переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

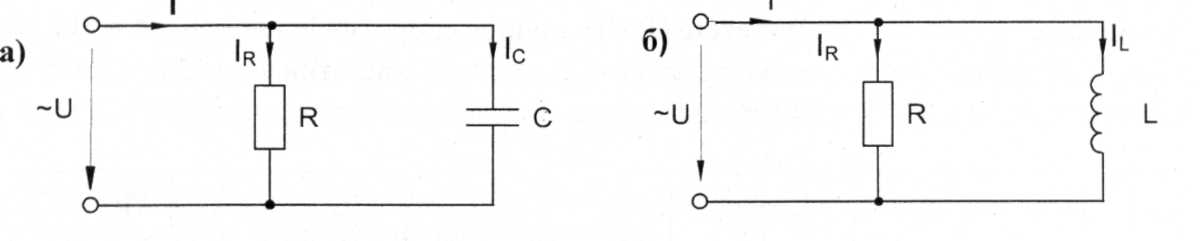
Рис.31.1

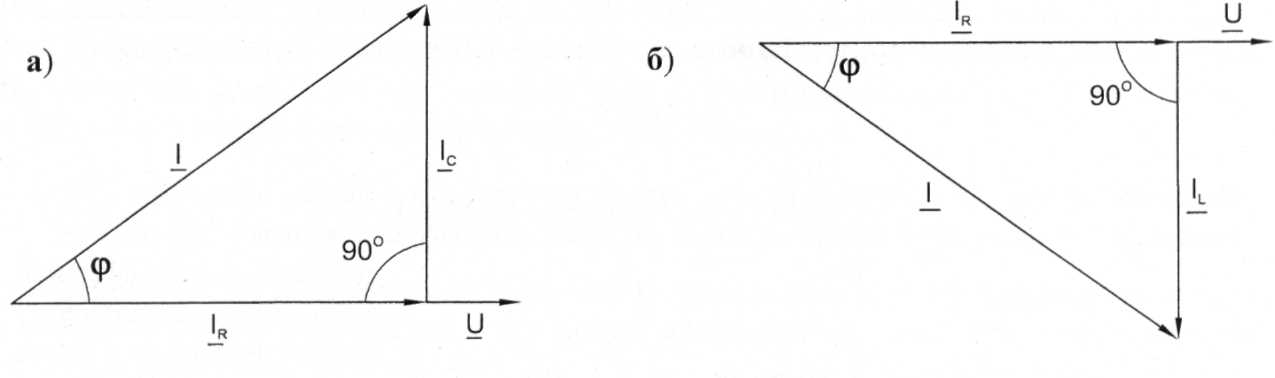
Рис.31.2

Общий ток цепи I разветвляется на ток в конденсаторе I_с или в индуктивности I_𝐋 (реактивная составляющая общего тока I_р) и ток в резисторе (активная составляющая I_а). Причём, ток в сопротивлении совпадает с напряжением по фазе, а ток в реактивном элементе сдвинут относительно напряжения на 90° (в ёмкости опережает, а в индук­тивности отстаёт). Сложение этих токов можно произвести с помощью векторной диа­граммы токов (рис. 31.2а и б).

Из векторных диаграмм следует, что в цепи с конденсатором

I= и φ = - arctg (I с /I_а).

Здесь I_а=U/R=U×G, a Ic=U/Xc=U ×В_с,

где G=l/R - активная проводимость, а Вс=1/Хс - ёмкостная проводимость. Поэтому

I=U = U ×Y и φ = - arctg (B_c/G ),

где Y= - полная проводимость, а φ<0, т.е. ток опережает напряжение.

Аналогично, в цепи с индуктивностью:

I= =U = U ×Y,

где Y= и φ = arctg (B_l/ G)>0

т.е. ток отстаёт от напряжения.

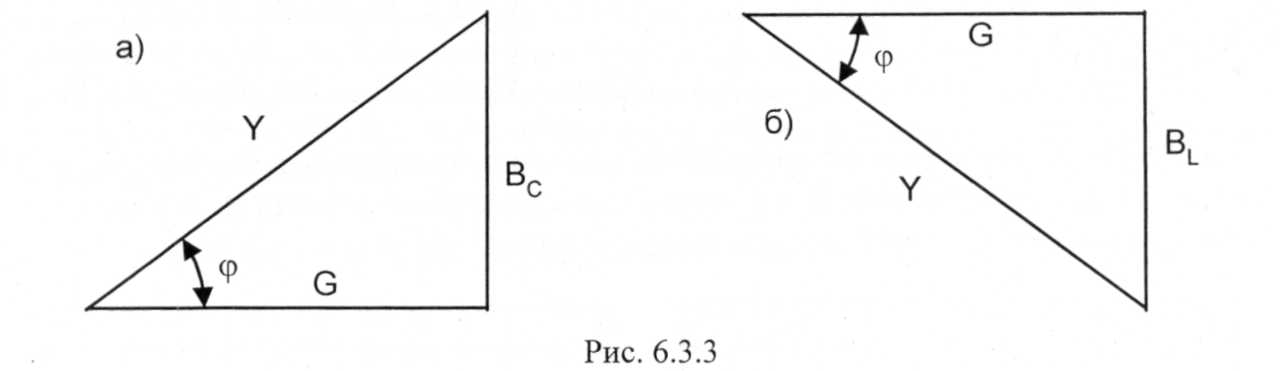
Рис.31.3

Из треугольников проводимостей следует , что

G = Y ×cosφ; B_с= Y× sinφ и B_l = Y ×sinφ.

Порядок проведения работы

Задание

Для цепи с параллельным соединением резистора и конденсатора, а также резистора и индуктивности измерьте потребляемую активную мощность, действующие значения тока в резисторе I_а и реактивном элементе I_р и ток I. Рассчитайте угол сдвига фаз φ, полную проводимость цепи Y, реактивную проводимость В и активную проводимость G, постройте векторную диаграмму.

Порядок выполнения эксперимента

• Соберите цепь согласно схеме (рис. 31.4), подсоедините регулируемый источник синусоидального напряжения и установите максимальную амплитуду синусоидаль­ного напряжения с частотой f = 1 кГц.

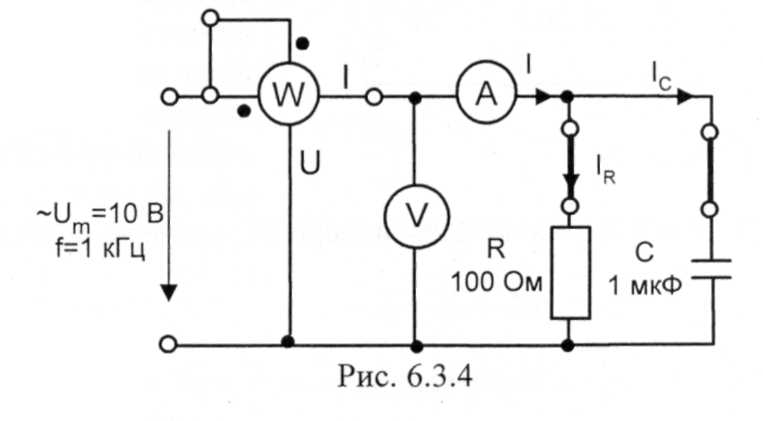
Рис.31.4

• Выполните измерения активной мощности, действующих значений токов и напряже­ний, указанных в табл. 31.1. При измерении токов подключайте мультиметр вместо перемычек, показанных на схеме.

Таблица 31.1

Цепь	Измерения					Расчет
	Р	U	I а	I р	I		φ	G	В	Y
	Вт	В	В	В	А		Град.	См	См	См
Ц Цепь с конденсатором ро
Це Цепь с катушкой

• Вычислите: фазовый угол φ= arctg (P/(U×I)),

• полную проводимость цепи Y =I/ U,

• ак­тивную проводимость цепи G = Y ×cos φ,

• ёмкостную проводимость Вс = Y ×sin φ .

• Выберите масштаб и постройте векторную диаграмму токов. (рис31.5).

Цепь с конденсатором М_I =….мА/дел Цепь с катушкой М_I =….мА/дел

Рис.31.5

• З амените в схеме конденсатор на катушку индуктивности с малым активным сопро­тивлением (рис.31.6). В качестве такой катушки используйте обмотку 300 витков разборного трансформа­тора.

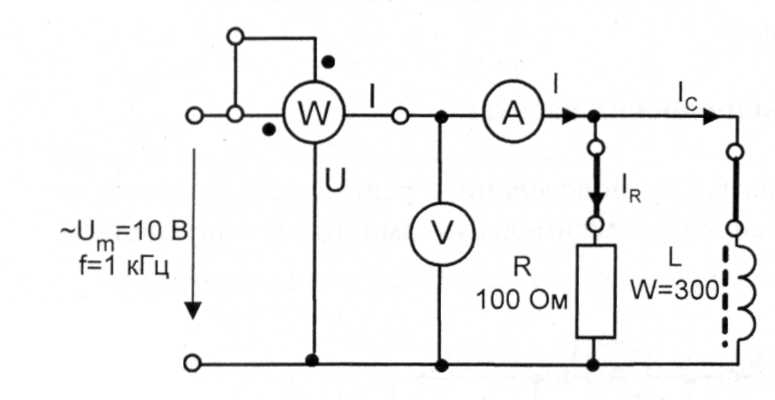
Рис.31.6

• Чтобы создать не­ магнитный зазор в магнитопроводе, вставьте между двумя частями сердечника квадратики обычной писчей бумаги в один или два слоя.