Порядок проведения работы

Задание

Убедитесь путем измерения тока и напряжения, что при последовательном соедине­нии катушек эквивалентная индуктивность цепи равна сумме индуктивностей, а при параллельном соединении она меньше индуктивности наименьшей катушки,.

Порядок выполнения эксперимента

• Соберите цепь с последовательным соединением катушек (рис. 27.1) и измерьте с помощью мультиметра действующие значения тока в цепи, приложенного напря­жения и напряжения на каждой катушке. Результаты измерений занесите в табл.27.1

Рис.27.1

• Вычислите индуктивные сопротивления X_{l э}, X_l1 X_l2, X_lз по формуле Xl=U/I.

• Определите индуктивности отдельных катушек и эквивалентную индуктивность цепи по формуле L = ω×Х _L, где ω = 2πf = рад/с. Проверьте вычислениями величину эквивалентной индуктивности L_э, найденную экспериментально.

Таблица 27.1

I= …	Х L =U/I,	L= ω×Х L,	Проверка
мА	Ом	мГн
U, В			Lэ = L 1 + L 2 + L 3 =
U L1,B			……………
U L2,B
U L3,B

• Соберите цепь с параллельным соединением катушек (рис. 27.2). Предусмотрите в схеме перемычки для измерения токов мультиметром. Включите регулируемый ис­точник синусоидального напряжения с параметрами U_m = 10 В и f = 1 кГц.

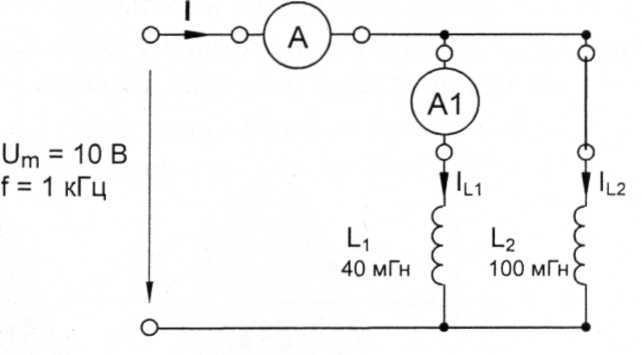
Рис. 27.2

• Измерьте мультиметром общий ток цепи I, токи параллельных ветвей I₁, I₂, и на­пряжения на входе цепи U, занесите данные измерений в табл. 27.2

• Вычислите индуктивные реактивные сопротивления X_{l э}, X_l1 X_l2, X_lз по формуле Xl=U/I.

• Определите индуктивности катушек и эквивалентную индуктивность цепи по фор­муле L = ω×Х _L, где ω = 2πf = рад/с.

• Проверьте вычислениями величину эквивалентной индуктивности L_э, найденную экспериментально

Таблица 27.2

U =… В	Х L =U/I,	L= ω×Х L,	Проверка
	Ом	мГн
I, мА			LЭ = (L1 × L2)/( L1 +L2) ……………………
I1 мА
I2, мА

Контрольные вопросы

1. Как определить эквивалентную индуктивность при параллельном и последовательном соединении катушек на основании результатов измерений.

2. Что означает сочетание «идеальная катушка»?

3. Как распределяются токи и напряжения на отдельных катушках, относительно их индуктивностей, при параллельном соединении?

4. Как распределяются токи и напряжения на отдельных катушках, относительно их индуктивностей, при последовательном соединении?

ЛАБОРАТОРНАЯ РАБОТА № 28

Мощности в цепи синусоидального тока

Цель работы: 1. Исследовать мощности цепи переменного тока.

2. Составить баланс мощностей.

В результате выполнения лабораторной работы студент должен:

знать: - формулы мощностей цепи переменного тока

уметь: - собирать электрические цепи по схемам;

- производить измерения тока и напряжения при помощи мульти

метра;

- производить измерения активной мощности при помощи ватт-

метра

- на основании измерений и расчётов составлять баланс

мощностей

Оборудование: лабораторный стенд.

Краткие теоретические сведения

На рис. 28.1а изображена произвольная пассивная цепь синусоидального тока с двумя зажимами для подключения источника питания. В общем случае, ток и напряжение на входе этой цепи сдвинуты по фазе на угол φ:

u=U_msin(ωt); i=I_msin(ωt-φ).

Мгновенная мощность, потребляемая цепью от источника:

p=ui= U_mI_msin(ωt)sin(ωt-φ)=U_mI_mcosφ-U_mI_mcos(2ωt-φ).

График изменения этой мощности представлен на рис. 28.1.6 вместе с графиками изменения тока и напряжения. Мощность колеблется с двойной частотой. Большую часть периода она имеет положительное значение, а меньшую - отрицательное. Отри­цательное значение мощности свидетельствует о возврате части накопленной в конден­саторах и катушках энергии в питающий цепь источник энергии.

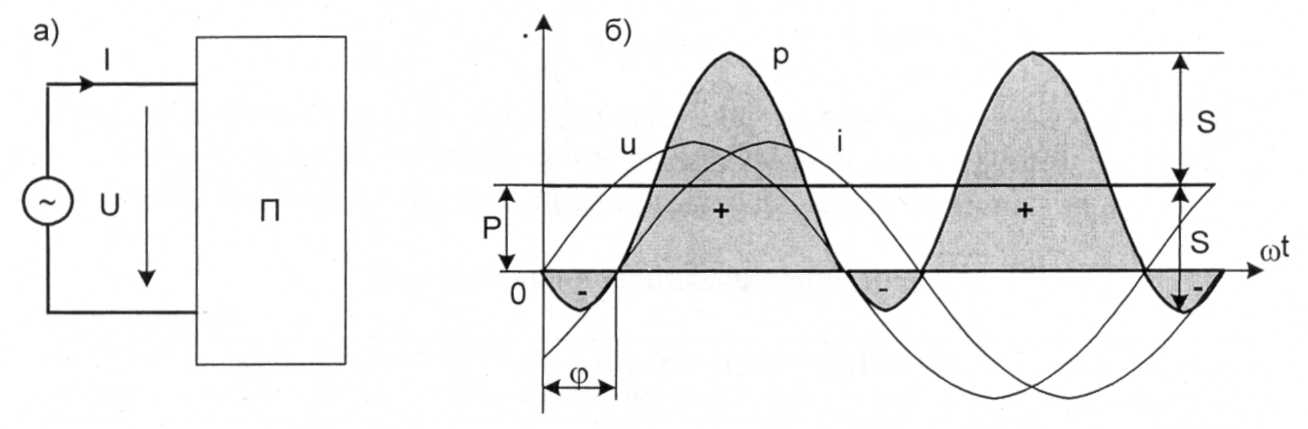
Рис.28.1

Среднее значение потребляемой мощности

P=UIcosφ=I²R

называется активной мощностью. Она характеризует среднюю скорость преобразо­вания электрической энергии в другие виды энергии. Потребляемая в пассивной цепи активная мощность имеет всегда положительное значение. Она измеряется ваттметром, схема включения которого в цепь показана на рис. 28.3. Единицей измерения активной мощности является ватт (Вт).

Амплитуда переменной составляющей мощности

S=UI=I²Z

называется полной мощностью. Она характеризует максимальную мощность, на кото­рую должен быть рассчитан источник для питания данной цепи. Её иногда называют кажущейся, габаритной или аппаратной мощностью. Единицей её измерения яв­ляется вольт-ампер (ВА). Здесь U = IZ, где Z = - полное сопротивление це­пи синусоидального тока.

Величина Q=UIsinφ=I²X

называется реактивной мощностью. Она характеризует максимальную скорость об­мена энергии между источником и цепью. Она может быть как положительной (при φ>0, т.е. в активно-индуктивной цепи), так и отрицательной (при φ<0, т.е. в активно-ёмкостной цепи). В связи с этим иногда говорят, что индуктивность потребляет «реактивную энергию», а ёмкость вырабатывает её. Реактивная мощность измеряется в вольт-амперах реактив­ных (вар).

В электрической цепи синусоидального тока выполняется баланс как активных, так и реактивных (но не полных!) мощностей, т. е. сумма мощностей всех источников рав­на сумме мощностей всех потребителей:

ΣР_ист. = ΣР_потр

ΣQ_ист = ΣQ_noтр

Соотношения между различными мощностями в цепи синусоидального тока можно наглядно представить в виде треугольника мощностей (рис. 28.2).

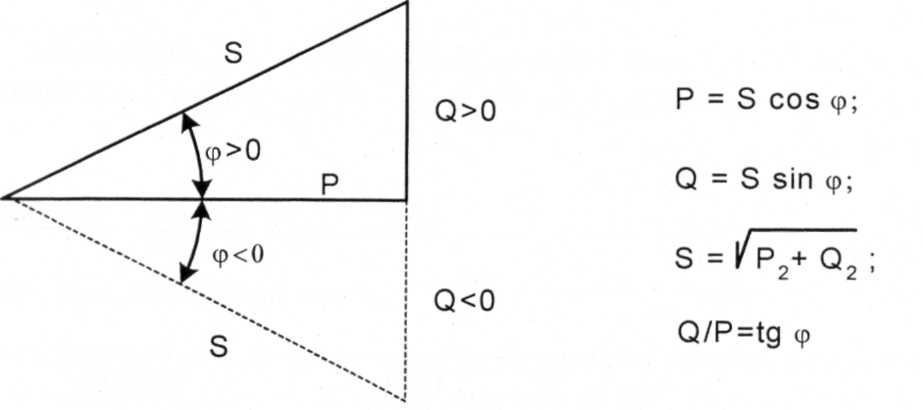
Рис.28.2

Порядок проведения работы

Задание

Измерьте токи, напряжения и мощность в разветвлённой цепи синусоидального тока. Расчётом проверьте баланс активных и реактивных мощностей.

Порядок выполнения эксперимента

Измерьте омметром активное сопротивление катушки индуктивности 40мГн:

R_K = Ом.

• При частоте = 500 Гц вычислите реактивные сопротивления катушки

L=40 мГн и конденсатора С=1 мкФ:

X_L=2πfL= Ом;

Xc=l/(2πfC) = Ом.

• Соберите цепь согласно схеме (рис. 28.3), предусмотрев в ней перемычки для измерения токов мультиметром. Подайте на схему синусоидальное напряжение 500 Гц и установите максимальную амплитуду, которую может дать генератор.

• Запишите в табл. 28.1 значения токов I_rl, I_r, I_c и мощности, отдаваемой

источником Р _ист. Вычислите S _ист ⁼ UI и Q _ист ⁼ и запишите в таблицу значение Q _ист.

Таблица 28.1

Ветвь	Rk	R	С	Баланс мощностей, мВт, мвар
I, I, мА
P=I2R,mBt			0	Р ист		ΣРпотр
Q=I2X, мВАр		0		Q ист t		ΣQnoтр

• Вычислите по приведённым в табл.28.1 формулам значения активной и реактивной мощностей каждого потребителя. Вычислите сумму активных и алгебраическую сумму реактивных мощностей потребителей и проверьте баланс мощностей.

Контрольные вопросы

1. Какая мощность называется активной?

2. Какая мощность называется реактивной?

3. Потребители и источники реактивной мощности.

4. Что характеризует полная мощность?

5. Баланс мощностей в цепи переменного тока.

6. Треугольник мощностей.

ЛАБОРАТОРНАЯ РАБОТА № 29

Последовательное соединение резистора и конденсатора, резисто­ра и катушки индуктивности

Цель работы: 1. Исследовать неразветвлённые электрические цепи

переменного тока.

2. Построить векторные диаграммы токов и напряжений

для каждой исследуемой цепи.

В результате выполнения лабораторной работы студент должен:

знать: - основные законы электротехники

уметь: - собирать электрические цепи по схемам;

- производить измерения тока и напряжения при помощи мульти-

метра;

- производить измерения активной мощности при помощи ватт-

метра

- строить векторные диаграммы

Оборудование: лабораторный стенд.

Краткие теоретические сведения

Когда к цепи (рис29.1) с последовательным соединением резистора и конденсато­ра (а) или резистора и катушки индуктивности (б) подается переменное синусоидаль­ное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи, а напряжение на входе цепи равно сумме напряжений на двух компонентах. По­скольку эти два напряжения сдвинуты относительно друг друга по фазе, непосредст­венное сложение их действующих значений или амплитуд невозможно. Необходимо либо складывать мгновенные значения этих напряжений, либо векторы, соответствую­щие этим напряжениям, как показано на рис. 29.2 а и б.

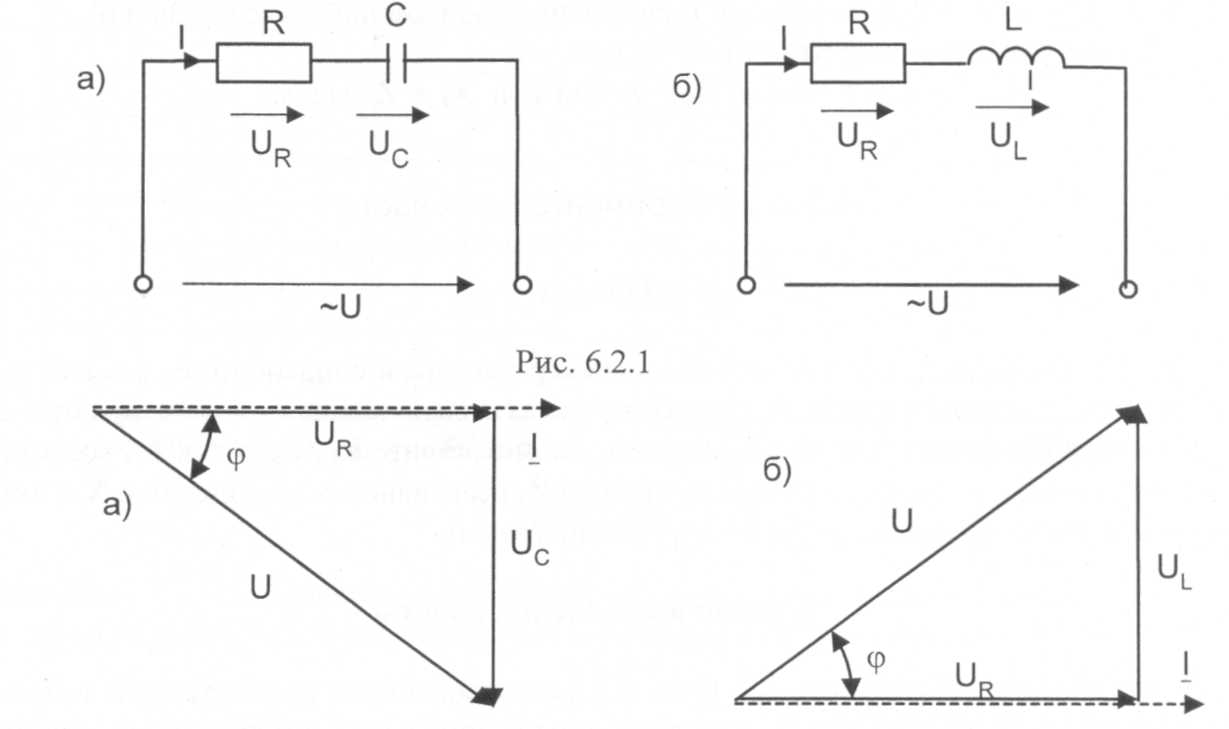
Рис.29.1

Рис.29.2

Вектор напряжения на конденсаторе U_c отстаёт от вектора тока I на 90⁰, а вектор на­пряжения на индуктивности U_l опережает ток на 90°. Из векторных диаграмм следует, что в цепи с конденсатором

U = , φ = -arctg(U_c/ U_r).

Поскольку U _а = R× I, a Uc = Xc×I, получаем

U = = I ×Z и φ = -arctg(X_c/ R),

где Z = - полное сопротивление цепи, и φ<0, т.е. ток опережает напряже­ние.

Аналогично, в цепи с индуктивностью:

U = , = = I ×Z, где

Z = , φ = arctg ( R)>0,

т.е. ток отстаёт от напряжения.

Если каждую сторону треугольника напряжений разделить на ток, то получим треугольник сопротивлений, подобный треугольнику напряжений, (рис.29.3 а и б). Из треугольников сопротивлений следует, что

R = Z × cos φ, Хс = Z × sin φ и Xl = Z × sin φ

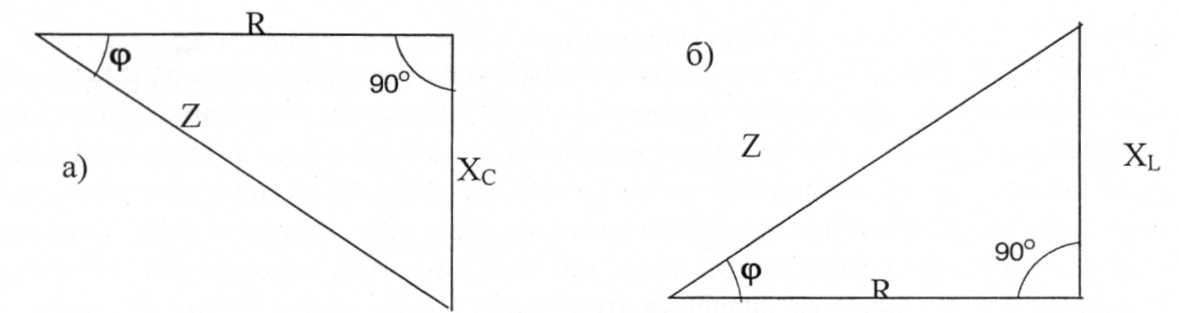
Рис.29.3

Порядок проведения работы

Задание

Для цепи с последовательным соединением резистора и конденсатора, а также рези­стора и индуктивности измерьте потребляемую активную мощность, действующие зна­чения напряжений на резисторе U_а и реактивных элементах U_р (Uc и Ul) и ток I. Рассчитайте угол сдвига фаз φ, полное сопротивление цепи Z, реактивное сопротивление X и актив­ное сопротивление R, постройте векторную диаграмму.

Порядок выполнения эксперимента

• Соберите цепь согласно схеме (рис. 29.4), подсоедините регулируемый источник синусоидального напряжения и установите максимальную амплитуду синусоидаль­ного напряжения с частотой f = 1 кГц.

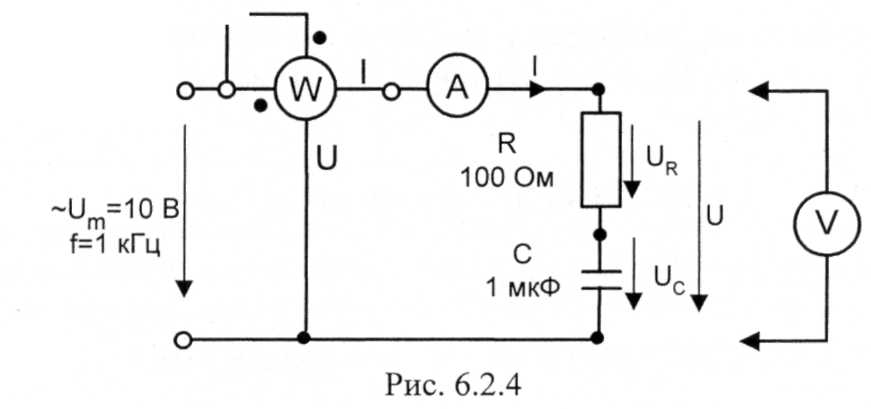
Рис.29.4

• Выполните измерения активной мощности, действующих значений тока и напряже­ний, указанных в табл. 29.1. При измерении напряжений подключайте мультиметр к различным участкам цепи.

Таблица 29.1

Цепь	Измерения					Расчет
	Р	U	Uа	Uр	I		φ	R	X	Z
	Вт	В	В	В	А		Град.	Ом	Ом	Ом
Ц Цепь с конденсатором ро
Це Цепь с катушкой

• Вычислите: фазовый угол φ= arctg (P/(U×I)),

• полное сопротивление цепи Z = U/I ,

• ак­тивное сопротивление цепи R = Zcos φ,

• ёмкостное сопротивление Хс = Zsin φ .

• Выберите масштаб и постройте векторную диаграмму напряжений (рис29.5).

Цепь с конденсатором М_U=….В/дел Цепь с катушкой М_U=….В/дел

Рис.29.5

• З амените в схеме конденсатор на катушку индуктивности с малым активным сопро­тивлением (рис.29.6). В качестве такой катушки используйте обмотку 300 витков разборного трансформа­тора.

Рис.29.6

• Чтобы создать не­ магнитный зазор в магнитопроводе, вставьте между двумя частями сердечника квадратики обычной писчей бумаги в один или два слоя.