небазисная

базисная переменная

небазисная переменная

Базисные переменные

По условию нашей задачи , а в решении только две базисные переменные положительны, следовательно, имеем вырожденное ДБР (так как у него количество положительных координат меньше ).

с) Рассмотрим множество векторов - .

Составим матрицу из этих векторов,

Значит множество векторов является базисом.

Выпишем уравнения системы с учетом того, что :

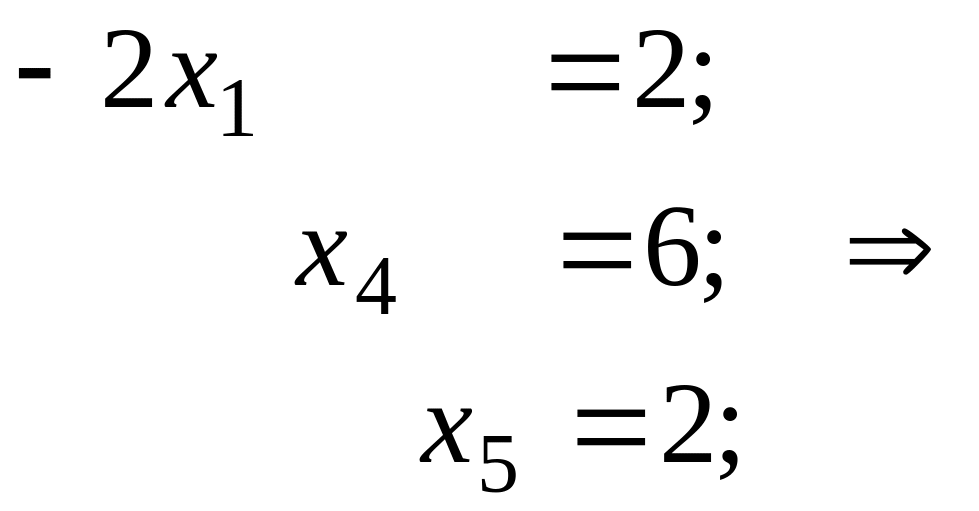
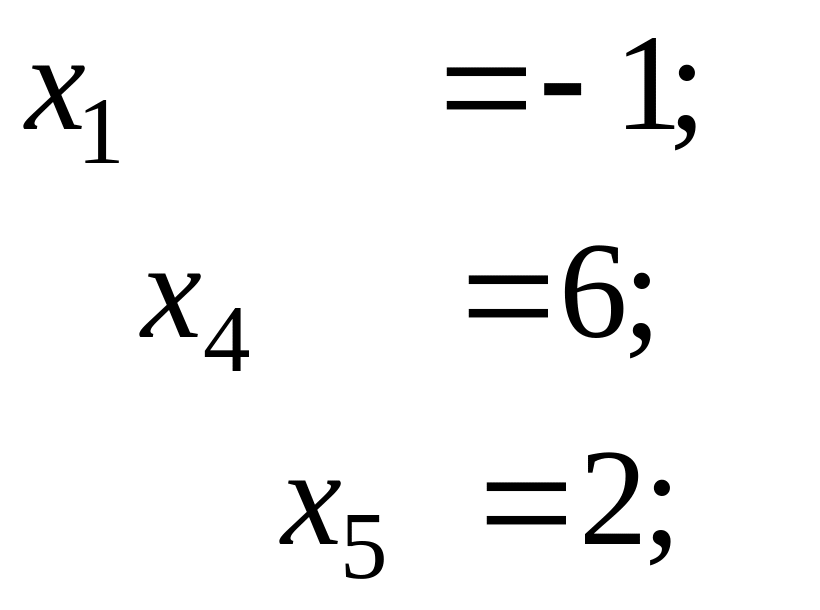
Таким образом, соответствующее базисное решение таково:

- базисная переменная

- небазисые переменные

- базисные переменные

Итак, базису соответствует решение, у которого одна переменная отрицательна, следовательно, имеем недопустимое базисное решение.

9. Табличный симплекс-метод

Пусть для исходной ЗЛП задано начальное ДБР, базис которого образуют первые m столбцов матри­цы A. Введем новую переменную z и с помощью элементарных преобразований Жордана-Гаусса преобразуем расширенную систему к диагональной форме относительно переменных z, x₁, x₂,…, x_m:

,

,

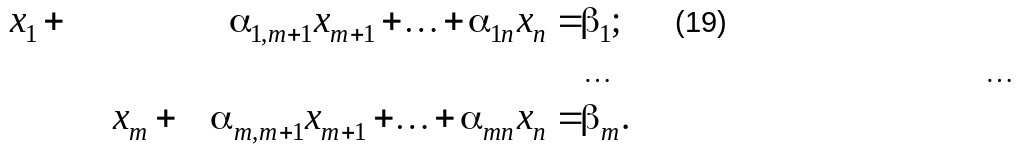
Диагональная форма (19) исходной системы ограничений, полученная при помощи преобразований Жордана-Гаусса, совпадает с диагональной формой (13)-(15), полученной матричным способом.

Диагональной форме (19) можно поставить в соответствие следующую таблицу, которая получила название симплекс-таблицы:

Таблица 1

БП	z	x1	…	xm	xm+1	…	xn	Решение
z	1	0	…	0		…		0
x1	0	1	…	0	1,m+1	…	1,n	1
…	…	…	…	…	…	…	…	…
xm	0	0	…	1	m,m+1	…	m,n	m

В левом столбце таблицы перечислены базисные переменные. В общем случае в этом столбце таблицы в i-ой строке будет записана переменная (x_B)_i.

Слева от таблицы указаны базисные переменные.

В общем случае в левом столбце таблицы в i-ой строке будет записана переменная .

Построенная таблица называется симплекс-таблицей. Она содержит всю информацию, необходимую для осуществления одной итерации симплекс-метода. Реализация симплекс-метода с помощью симплекс-таблицы называется табличным симплекс-методом.

По сути, симплекс-метод и табличный симплекс-метод соотносятся между собой как метод и алгоритм.

В дальнейшем столбец будем опускать, так как от итерации к итерации он не изменяется .

9.1. Схема табличного симплекс-метода

Шаг 0. Начальный шаг

Построить начальное ДБР исходной задачи.

Построить соответствующую этому ДБР симплекс-таблицу.

Шaг 1. Проверка условия оптимальности

ЕСЛИ коэффициенты z-строки

неотрицательны - в случае задачи на максимум

(неположительны - в случае задачи на минимум),

ТО прекратить вычисления: текущей симплекс-таблице соответствует оптимальное ДБР.

Шаг 2. Выбор переменной, вводимой в базис.

Среди коэффициентов выбрать отрицательный.

Пусть мы выбрали .

Переменная будет вводиться во множество базисных переменных, а -й столбец будет ведущим.

Шаг 3. Выбор переменной, выводимой из базиса

ЕСЛИ все коэффициенты ведущего столбца неположительные, то прекратить вычисления: целевая функция не ограничена сверху.

ИНАЧЕ выбрать переменную , которой соответствует минимум в выражении

_.

-ая строка называется ведущей.

Элемент таблицы на пересечении ведущих строки и столбца называется ведущим элементом.

Шаг 4. Переход к новому ДБР

В столбце «Базисные переменные» в q-ой строке записать переменную .

Используя элементарные преобразованиям Гаусса, исключить переменную из всех строк, кроме ведущей (в новой симплекс-таблице добиться того, чтобы на месте ведущего элемента стояла единица, а все остальные коэффициенты ведущего столбца равнялись нулю).

Перейти на шаг 1.