12.3. Особые случаи, возникающие при применении двухэтапного мтода

Рассмотрим примеры особых случаев, которые встречаются при решении задачи двухэтапным симплекс-методом.

Пример 12.3 (Вырожденность).

Пусть имеем математическую модель:

min z=x₁+x₂ (12.1)

-x₁ + x₂  1 (12.2)

2x₁ + x₂  4 (12.3)

x₂  1 (12.4)

x₁,x₂ 0 (12.5)

Приведем задачу к канонической форме:

min z= x₁ + x₂ +0s₁ +0s₂ +0s₃ (12.6)

-x₁ + x₂ -1s₁ = 1 (12.7)

2x₁+ x₂ +1s₂ = 4 (12.8)

x₂ -1s₃ =1 (12.9)

x₁,x_{2 ,}s₁,s₂,s₃0 (12.10)

x₁

x₂

(2.2)

(2.3)

(2.4)

1.Рис. 4.12.2

x₁

x₂

(12.3)

(12.2)

(12.4)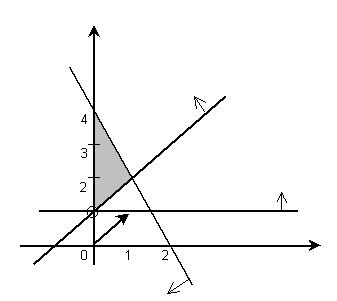

Этап 1

1. Введем искусственные переменные в ограничения типа “” и “=”. В нашей задаче это ограничения (12.2) и (12.4). Назовем искусственные переменные R₁ и R₂ соответственно. Тогда модель (12.6)-(12.10) будет иметь такой вид:

min z= x₁+ x₂ +0s₁ +0s₂ +0s₃ +0R₁ +0R₂ (12.11)

-x₁+ x₂ -1s₁ +R₁ = 1 (12.12)

2x₁+ x₂ +1s₂ = 4 (12.13)

x₂ -1s₃ +R₂ = 1 (12.14)

x₁,x_{2 ,}s₁,s₂,s₃0 (12.15)

2. R₁ и R₂ выражазим из соответствующих уравнений (12.12), (12.14):

R₁ = 1 + x₁- x₂ +1s₁

R₂= 1 - x₂ +1s₃

Получим такую целевую функцию:

r = R₁ + R₂ = 2 + x₁ -2x₂ +1s₁ +1s₃

Перепишем целевую функцию в виде:

r - 1x₁ + 2x₂ -1s₁ -1s₃ = 2

3. Построим начальную таблицу двухэтапного симплекс-метода.

Базисные переменные	x1	x 2	s1	s2	s3	R1	R2	Решение
r(min)	-1	2	-1	0	-1	0	0	2
z	-1	-1	0	0	0	0	0	0
R1	-1	1	-1	0	0	1	0	1	1
R2	0	1	0	0	-1	0	1	1	1
s2	2	1	0	1	0	0	0	4	4

Согласно условию оптимальности вводим в базис переменную x_{2 .} На данном этапе невозможно однозначно определить переменную, которою необходимо выводить из базиса согласно условию допустимости.

Мы можем вывести из базиса как переменную R₁, так и переменную R_2, потому что отношения коэффициентов столбца решений к положительным коэффициентам рабочего столбца одинаковы, и равны единице. Остановим свой выбор на переменной R_1. В результате операции замещения получачим таблицу:

Базисные переменные	x1	x2	s1	s2	s3	R1	R2	Решение
r(min)	1	0	1	0	-1	-2	0	0
z	-2	0	-1	0	0	1	0	1
x2	-1	1	-1	0	0	1	0	1
R2	1	0	1	0	-1	-1	1	0	0
s2	3	0	1	1	0	-1	0	3	1

Одна из базисных переменных (R₂) равна нулю. Это означает, что соответствующее решение является вырожденным. С практической точки зрения ситуация полностью объясняется присутствием в модели одного избыточного ограничения. Продолжаем решение задачи по алгоритму симплекс- метода.

Поскольку не все коэффициенты целевой функции отрицательные, то продолжаем выполнять итерации симплекс-метода. Согласно условию оптимальности вводим в базис переменную x₁ и, согласно условию допустимости, выводим из базиса переменную R_2. Получим таблицу:

Базисные переменные	x1	x2	s1	s2	s3	R1	R2	Решение
r(min)	0	0	0	0	0	-1	-1	0
z	0	0	1	0	-2	-1	2	1
x2	0	1	0	0	-1	0	1	1
x1	1	0	1	0	-1	-1	1	0
s2	0	0	-2	1	3	2	-3	3

Поскольку из базиса выведены все искусственные переменные, то мы получили вырожденное допустимое решение исходной задачи. То есть в текущей точке присутствуют избыточные ограничения, и при этом среди них нет линейно-зависимых.

Итак, если в результате минимизации целевой функции r из базиса выводятся все искусственные переменные, и хотя бы одна из базисных переменных равна 0, то в текущей точке есть избыточное ограничение, и при этом среди них нет линейно-зависимых.

Этап 2

Выполним последнюю итерацию:

Базисные переменные	x1	x2	s1	s2	s3	Решение
z(min)	0	0	1	0	-2	1
x2	0	1	0	0	-1	1
x 1	1	0	1	0	-1	0
s2	0	0	-2	1	3	3

Согласно условию оптимальности вводим в базис переменную s₁ и согласно условию допустимости выводим из базиса переменную x_1. Получаем таблицу:

Базисные переменные	x1	x2	s1	s2	s3	Решение
z(min)	-1	0	0	0	-1	1
x2	0	1	0	0	-1	1
s1	1	0	1	0	-1	0
s2	2	0	0	1	1	3

Данная таблица - оптимальная, потому что в строке z коэффициенты при небазисных переменных – отрицательные (условие оптимальности для задачи на минимум). Задача решена.

Ответ: x₁=0, x₂ =1, z = 1.