МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ УКРАИНЫ
«КиЕвский ПолИтехнИчЕСКий Институт»
Симплекс-метод
МетодичЕСКИЕ УКАЗАНИЯ
для самостоятельной работы
по дисциплине «Математические методы исследования операций»
для студентов специальности
«Информационные управляющие системы и технологии»
Утверждено
На заседании кафедры автоматизированных систем обработки информации и управления Протокол № 1 от 29.08.2012
Киев 2012
Симплекс-метод. Методические указания для самостоятельной работы по дисциплине «Математические методы исследования операций» для студентов специальности «Информационные управляющие системы и технологии» / Сост.: Е.Г. Жданова. – К.: НТУУ “КПИ”, 2012. – 70 с.
Учебное издание
Симплекс-метод
МетодичЕСКИЕ УКАЗАНИЯ
для самостоятельной работы
по дисциплине «Математические методы исследования операций»
для студентов специальности
«Информационные управляющие системы и технологии»
Составитель Жданова Елена Григорьевна
Ответственный редактор В.А. Тихонов
Рецензенты: C.Ф. Теленик
В.Н. Кузнецов
Методические указания содержат теоретические основы симплекс-метода – основного метода решения задач линейного программирования. Приведены основные теоремы линейного программирования, схемы алгоритмов симплекс-метода и табличного симплекс-метода. Рассмотрены методы нахождения начального допустимого базисного решения, особые случаи использования симплекс-метода. Приведены примеры решения задач линейного программирования и задания для контрольных работ.
Содержание
на заседании кафедры автоматизированных систем обработки информации и управления Протокол № 1 от 29.08.2012 1
1. Формы ЗЛП 5
2. Эквивалентность различных форм ЗЛП 6
Упражнения 10
3. Основные свойства ЗЛП 11
4. Идея симплекс – метода 13
5. Преобразованная задача 13
Получили так называемую преобразованную задачу. Обозначив 15
6. Способ перехода от одного ДБР к другому 15
7. Условие оптимальности ДБР 17
8. Схема симплекс-метода 19
базисные переменные 21
9. Табличный симплекс-метод 22
9.1. Схема табличного симплекс-метода 23
10. Примеры реализации табличного симплекс-метода 24
Пространство решений данной задачи показано на рис.1. 24
Полученные результаты удобно представить в виде таблицы. 26
Таблица 3 26
Рисунок 2 34
11. Искусственное начальное решение 34
11.1. М - метод 35
11.2. Двухэтапный метод 39
Пример 11.2. 43
44
Этап 1. 44
Этап 2 46
12. Вырожденность 47
12.1 Вырожденное оптимальное решение 47
12.2. Промежуточное вырожденное решение 50
12.3. Особые случаи, возникающие при применении двухэтапного мтода 53
Пример 12.3 (Вырожденность). 53
Этап 1 54
Этап 2 55
Пример 12.4 (Наличие избыточных ограничений, которые есть линейной комбинацией других ограничений.) 56
Этап 1 56
13. Альтернативные оптимальные решения 58
14. Неограниченность пространства решений и целевой функции 61
15. Отсутствие допустимых решений 64
68
Этап 1 68
16.Задания для контрольной работы 70
Список литературы 71
1. Формы злп
Задача математического программирования вида:
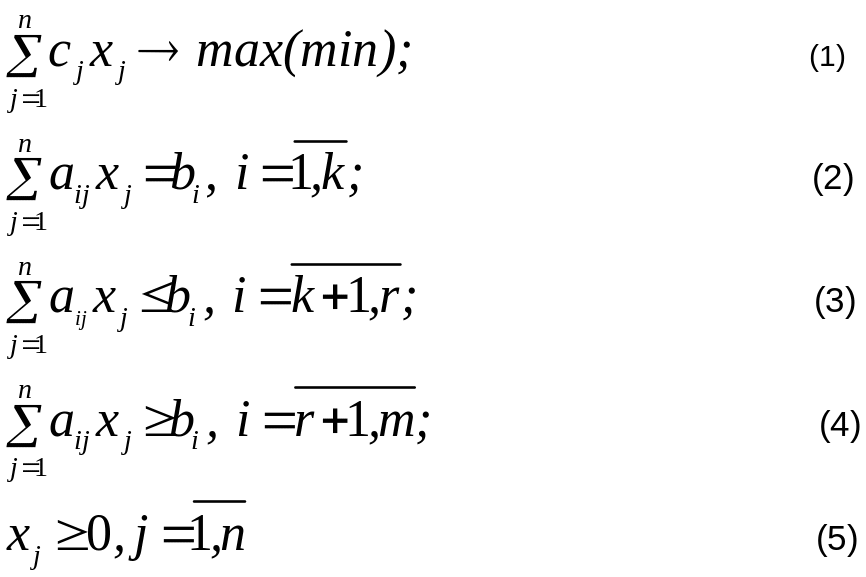
называется задачей линейного программирования (ЗЛП).
Основными допущениями, принимаемыми при построении линейных моделей, является пропорциональность, аддитивность, неотрицательность.
В зависимости от вида ограничений различают три основные формы ЗЛП.
ЗЛП вида (1)–(5) называется общей ЗЛП.
ЗЛП вида:
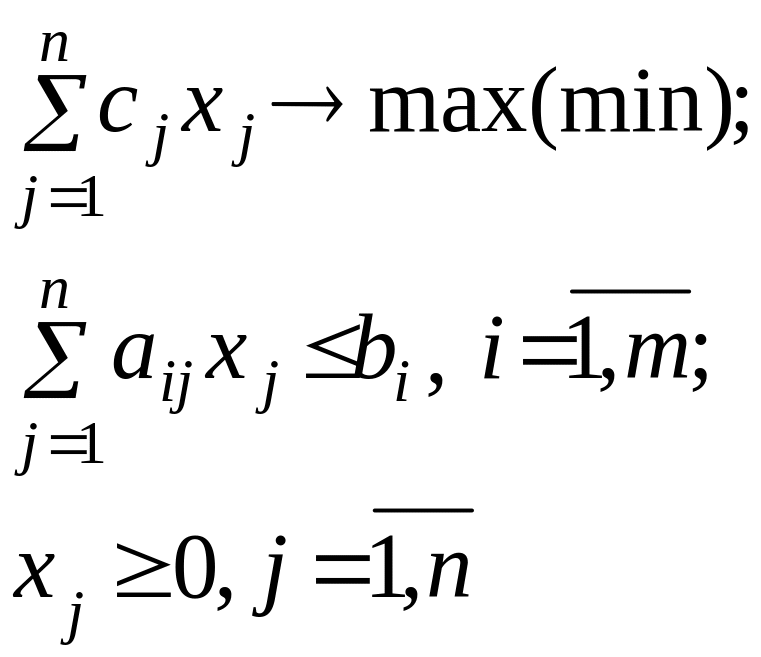
называется стандартной ЗЛП. В матричном виде она записывается следующим образом:
где
ЗЛП вида:
называется канонической ЗЛП. Она может быть записана в матричном виде следующим образом:
Метод решения ЗЛП разработан для задачи в канонической форме.