7. Дискретные линейные системы с постоянными параметрами. Уравнение циклической свертки.

Теория дискретных линейных систем связана с описанием и обработкой временных или частотных последовательностей и проектированием систем цифровой обработки сигналов, например фильтров

Линейные системы с постоянными параметрами

Линейная система - это система, к которой применим принцип суперпозиции и определяется она следующим образом. Если X₁(n) и X₂(n) - некоторые входные последовательности, а Y₁(n) и Y₂(n) - соответствующие им выходы линейной системы, то при подаче на вход последовательности aX₁(n) + bX₂(n) на выходе образуется последовательность aY₁(n) + bY₂(n), где а и b - произвольные постоянные.

Система с постоянными параметрами характеризуется тем, что если входной последовательности X(n) соответствует выход Y(n), то входной последовательности X(n-n₀) при любых n₀ соответствует на выходе Y(n-n₀). Это свойство называется инвариантностью во времени.

Дискретная система по существу задает алгоритм преобразования одной последовательности (входной X(n)) в другую (выходную Y(n)).

Циклические и линейные свертки

Прямые способы вычисления произведения многочленов содержат число умножений и сложений, примерно равное произведению степеней многочленов, LN; возможны, однако, другие способы вычисления такого произведения, содержащие меньшее число вычислений.

Циклическая свертка, s M = 8 (х) d (x) (mod хп — 1), рициенты даются п —

где deg g (х) = deg d (x) = п — 1, коэфствами si = Е ?(«-*> A. i = 0,6=0

и двойные скобки обозначают вычисления по модулю л, если вычислять ее прямо по выписанным формулам, содержит п2 умножений и я (п — 1) сложений. Циклическую свертку можно также вычислять как линейную свертку с последующим приведением

по модулю хп— Iх). Следовательно, эффективные способы вычисления линейной свертки приводят также к эффективным методам вычисления циклической свертки. Наоборот, эффективные методы вычисления циклической свертки можно легко превратить

в эффективные методы вычисления линейной свертки. Популярным способом вычисления циклической свертки является использование теоремы о свертке и дискретного преобразования Фурье. Согласно теореме о свертке в частотной области, Sh = GhDk, k = 0, ..., п— 1, так что свертку можно вычислять, выполняя последовательно преобразование Фурье, поточечное умножение и обратное преобразование Фурье

8. Уравнение апериодической свертки. Графическое представление вычисления свертки. Пример.

А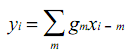 периодическая свертка (линейная) относятся к классу локальных преобразований. При этом как правило полагается, что размер вектора исходных данных значительно больше размера ядра свертки, что приводит к следующему выражению для вычисления любого отсчета результата:

Вычисление свертки лежит в основе корреляционного метода подавления помех. Сущность такого метода заключается в использовании различия между корреляционными функциями сигнала и помехи. Данный метод эффективен лишь в случае обработки периодических или квазипериодических сигналов. Рассмотрим сущность метода на примере, когда полезный сигнал является гармоническим, а помеха - типа белого гауссова шума [21]. Автокорреляционная функция сигнала является тоже гармонической и имеет ту же частоту. Метод автокорреляционного приема основан на анализе автокорреляционной функции принятого сигнала y(t)=x(t)+р(t). Если сигнал и помеха взаимно независимы (типичный для практики случай), то т.е автокорреляционная функция принятого сигнала равна сумме автокорреляционных функций сигнала и помехи. Метод корреляционного приема позволяет обнаружить полезный сигнал, который имеет мощность значительно меньшую, чем мощность помехи.

Пусть имеется два дискретных сигнала a(n),n=0..N-1, и b(n), n=0..M-1. В общем случае длины этих сигналов N  и M  могут отличаться. Линейной сверткой сигналов a(n)  и b(n) называется дискретный сигнал вида: Для вычисления линейной свертки сигналы a(n)  и b(n) сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что a(n)=0 при n<0  и n>N , а также b(n)=0  при n<0  и n>M.  Графическое представление:

Отсчеты сигнала b(n)  сдвигаются относительно отсчетов последовательности a(n) все возможные перекрывающиеся отсчеты почленно перемножаются и складываются. Приведен пример вычисления линейной свертки двух сигналов a(n)=[2,1,3,-1] длиной 4 отсчета и b(n)=[-1,1,2] длиной 3 отсчета.

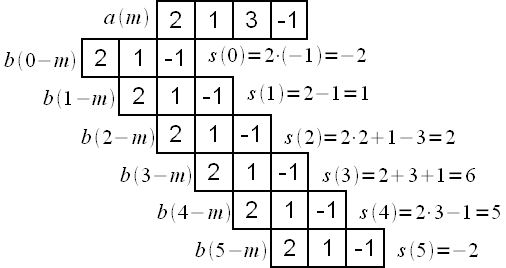
Необходимо отметить, что сигнал b(n)  при вычислении свертки отражается слева-направо, поскольку b(0)= -1 самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.