48. Структурная схема процессора для вычисления n-мерного сигнала. Пример бпф с прореживанием по времени

Рассмотрим идею БПФ с прореживанием по времени на примере деления набора отсчетов пополам.

Итак, пусть N — четное число. Выделим в формуле (6) два слагаемых, соответ­ствующих элементам исходной последовательности с четными и нечетными но­мерами:

(8)

Введем обозначения и , а также вынесем из второй суммы общий множитель :

(9)

Две суммы в (9) представляют собой ДПФ последовательностей {у(т)} (от­счеты с четными номерами) и {z(m)} (отсчеты с нечетными номерами). Каждое из этих ДПФ имеет размерность N/2. Таким образом,

(10)

где и — ДПФ соответственно последовательностей отсчетов с четными и нечетными номерами.

Так как ДПФ размерности N/2 дает лишь N/2 спектральных коэффициентов, непосредственно использовать формулу (10) можно только при 0 < n < N/2. Для остальных n (N/2 < n < N) следует воспользоваться периодичностью спектра дискретного сигнала (и, соответственно, периодичностью результатов ДПФ):

, Следовательно при n ≥ N/2 формула (10) представляется в виде:

11)

Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных ДПФ иллюстрируется на рис. 5.

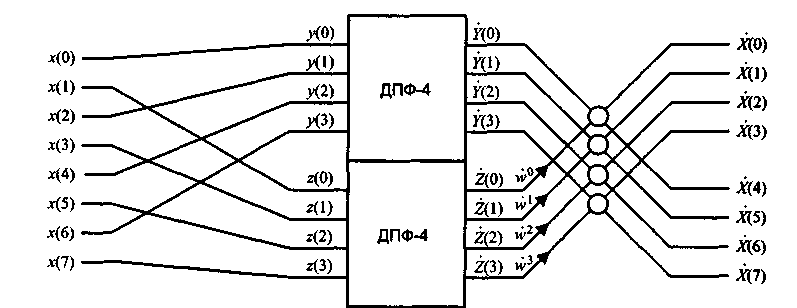
Рис. 5. Вычисление 8-точечного ДПФ с помощью двух 4-точечных ДПФ

Блоки, выполняющие на рис. 5. объединение результатов двух ДПФ, требуют дополнительных комментариев. Каждый такой блок имеет два входных и два выходных сигнала. Один из входных сигналов умножается на комплексную экспоненту , после чего суммируется со вторым входным сигналом и вычитается из него, формируя таким образом два выходных сигнала. Это соответствует реа­лизации формул (10) и (11). Данная операция получила название «бабочки». Расшифровка ее структуры представлена на рис. 6.

Рис. 6. Условное обозначение «бабочки» БПФ с прореживанием по времени (слева) и ее структурная схема (справа)

49. Дисперсионный принцип фильтрации трансформант. Пример.

Методы фильтрации трансформант и их сравнение.

Ошибка восстановления, связанная с усечением разложений, является функцией числа и относительной важности отбрасываемых коэффициентов преобразования, а также точности, используемой для представления значений сохраняемых коэффициентов. В большинстве систем трансформационного кодирования выбор оставляемых коэффициентов осуществляется либо детерминировано на основе анализа дисперсии значений коэффициентов по всем блокам (зональное кодирование), либо адаптивно – выбором коэффициентов с максимальными значениями (пороговое кодирование). Весь процесс, включающий усечение, квантование и кодирование коэффициентов, обычно называют представлением в двоичной форме.

Метод дисперсионного отбора трансформант основан на концепции теории информации о количестве информации как мере неопределенности. Коэффициенты преобразования с максимальной дисперсией содержат максимум информации, и, следовательно, должны сохраняться в процессе кодирования. Дисперсии могут быть вычислены либо на прямую из ансамбля массивов преобразованных блоков, либо на основании принятой модели изображения (например, марковской первого порядка).

В отличие от порогового способа фильтрации коэффициентов преобразования, когда передаются лишь те трансформанты, значения которых превышают фиксированный порог, дисперсионная фильтрация предполагает сохранение лишь М коэффициентов с наибольшими дисперсиями. В случае детерминированного способа отбора трансформант исключается необходимость передачи адресных кодовых слов. Значения передаваемых трансформант квантуются числом уровней, пропорциональным дисперсии соответствующего коэффициента. Такой способ отбора коэффициентов преобразования называют зональным или, детерминированным, т.к. в зависимости от локальных статистических характеристик исходного изображения выделяется совокупность трансформант, находящаяся в определенной области (зоне) спектра. Восстановленное изображение может быть представлено как функция своего прямого преобразования:

f’= ,

(1)

где - фильтрующая функция коэффициентов преобразования (определяет маску для отбора трансформант),

T(u,v) – функция двумерного преобразования исходного изображения,

- матрицы размером n n (ядра преобразования),

= 0, если T(u,v) удовлетворяет заданному критерию усечения

1. в остальных случаях

для u, v = 0, 1, 2,…, n-1.

Согласно формуле (1) зональный отбор коэффициентов может рассматриваться как умножение каждого коэффициента T(u,v) на соответствующие элементы зональной маски. Коэффициенты соответствуют единицам в точках значений отобранных максимальных дисперсий и нулям во всех остальных точках. Обычно коэффициенты с максимальной дисперсией располагаются вблизи начала координат преобразованного блока; типичный пример зональной маски представлен на рисунке .