45. Пороговая фильтрация коэффициентов преобразования Уолша-Адамара. Пример.

Для пороговой фильтрации вычисляется прямое двухмерное дискретное преобразование исходного фрагмента изображения размером (N N), затем выбирается порог (h) и для передачи по каналу связи выбираются те значения трансформант, для которых , остальные приравниваются к нулю.

Эффективность сжатия изображения можно оценить путем вычисления СКО.

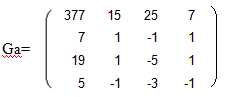
Пример порогового кодирования ДПУА для фрагмента изображения с корелляционно зависимой амплитудой сигнала изображения размером 4 4.

Фрагмент изображения – g; A – ядро ДПУА.

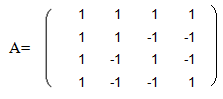
Вычисляется прямое двухмерное ДПУА согласно формуле:

Выбираем коэффициенты сжатия 1,77; 2,67; 4; 5,3; 8; 16. Соответственно им выбирается порог h. Трансформанты, удовлетворяющие условию |G|≥h, остаются, остальные приравниваются к нулю.

С помощью обратного спектрального преобразования восстанавливаем исходный фрагмент изображения, используя формулу:

Находим СКО (σ) восстановленного фрагмента изображения по формуле.

46. Описание границ объектов на изображениях посредством преобразований. Пример.

Существуют различные подходы к описанию границ. Сами границы также могут описываться различными параметрами, их еще называют дескрипторами. Среди наиболее простых и известных дескрипторов можно выделить – длину границы, описание границы с помощью четырехнаправленного цепного кода Фримана, Фурье-дескрипторы и т.д.

В этом материале нами будет рассмотрено описание границ некоторого объекта на основании преобразования Фурье. Рассмотрим это более детально.

Границу объекта можно представить в виде последовательности координатных пар

, (1)

где   – координаты некоторой точки границы; 

Каждую пару координат можно представить в виде комплексного числа

. (2)

Выражение преобразования Фурье для конечной последовательности   задается уравнением

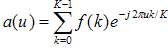, (3)

при u=0,1,2,...,K-1.

Коэффициенты a(u) описывают границу, и их называют дескрипторами границ.

Обратное преобразование Фурье, примененное к этим коэффициентам, позволяет восстановить границу  :

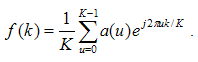 (4)

Если же при обратном преобразовании Фурье использовать не все K-1 коэффициенты ряда Фурье, а только их часть – R-1, то результатом восстановления будет следующее приближение последовательности  :

 (5)

Таким образом, результат   будет только приближенно описывать исходную последовательность  . Точность этого приближения будет зависеть от количества использованных коэффициентов Фурье.

Проиллюстрируем сказанное выше на конкретном примере.

47. Оценка вычислительной сложности бпф. Выигрыш в вычислительной сложности бпф.

Быстрое преобразование Фурье включает набор эффективных алгоритмов, предназначенных для вычисления ДПФ. Идея БПФ по своей природе заключается в следующем. Величина N, определяющая длину входной последовательности отсчетов, раскладывается на сомножители, затем вычисляются отдельные ДПФ меньших длин, чем N, из которых потом формируется выходная последовательность. Происходит так называемое расщепление исходного алгоритма на комбинацию подобных алгоритмов меньшего размера. БПФ содержит число мультипликативных операций (операций комплексного умножения) (N/2)log2N, число аддитивных операций (операций комплексного сложения) Nlog2N.

Вывод: Вычислительные преимущества БПФ по сравнению ДПФ следующие: БПФ содержит (N/2)log2N операций комплексного умножения в отличие от N2 при ДПФ, таким образом, вычислительная экономия составляет N2 / (N/2)log2N. Например, если N=1024, то экономия составляет 204,8 раза. БПФ содержит Nlog2N операций комплексного сложения в отличие от N(N-1) при ДПФ таким образом, вычислительная экономия составляет N(N-1) / Nlog2N. Например, если N=1024, то экономия составляет 102,3 раза.