29. Дпф. Свойства. Инвариантность дпф относительно сдвига по времени и частоте.

Дискретное преобразование Фурье.

Прямое преобразование:

, k =0, 1, …,N –1, где

W=e^-i2р/N – поворачивающий множитель

N – количество дискретных отсчетов сигнала

C(k) - N комплексных амплитуд синусоидальных сигналов

x(n) — измеренные значения сигнала которые являются входными данными для прямого преобразования и выходными для обратного

Обратное преобразование:

n =0, 1, …,N –1, где

W=e^i2р/N – поворачивающий множитель

Свойство инвариантности к частотному сдвигу

Пусть сигнал имеет спектр . Произведем циклический сдвиг спектра и рассмотрим ОДПФ, тогда:

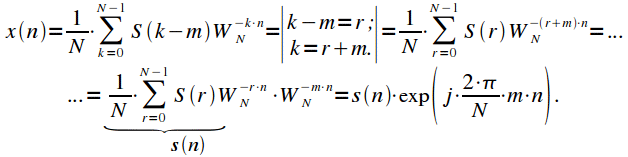
Таким образом получили, что сдвиг спектра осуществляется умножением сигнала на комплексную экспоненту. Важно отметить, что после умножения на комплексную экспоненту сигнал будет комплексным, а его спектр перестанет быть симметричным.

Свойство инвариантности к временному сдвигу

Пусть сигнал имеет спектр . Если сдвинуть сигнал циклически на отсчетов, т.е. , то спектр сдвинутого сигнала равен:

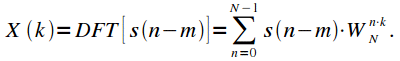
Введем замену переменной , тогда и выражение (4) можно переписать:

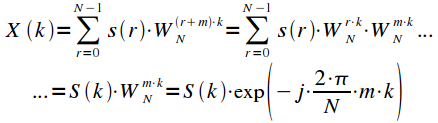
Таким образом циклический сдвиг сигнала на m приводит к повороту фазового спектра, а амплитудный спектр не меняется.

30.38 Вычислительнаясложностьдискретныхпреобразований: дпф, дпх, дпу-a, дкп.

вычислительная сложность для прямого и обратного преобразований равна:

1. в случае одномерного преобразования (умножение матрицы ядра преобразования на вектор входной последовательности):

- аддитивная =

- мультипликативная: = ;

здесь N – размерность преобразования.

2. в случае двумерного преобразования (умножение матрицы ядра преобразования на матрицу изображения и на матрицу ядра обратного преобразования):

- аддитивная = ;

- мультипликативная: = ;

В случае ДПФ вычислительная сложность увеличивается за счет того, что операции производятся над комплексными числами, так как одно комплексное умножение эквивалентно четырем операциям действительного умножения и двум операциям сложения.

Таким образом, для ДПФ вычислительная сложность равна:

1. для одномерного преобразования:

- аддитивная =

- мультипликативная: = ;

здесь N – размерность преобразования.

2. для двумерного преобразования:

- аддитивная = ;

- мультипликативная: = ;

31. Алгоритм быстрого преобразования Фурье. Алгоритм разделения входной последовательности на части. Посмотреть48

Быстрое преобразование Фурье включает набор эффективных алгоритмов, предназначенных для вычисления ДПФ. Идея БПФ: Величина N, определяющая длину входной последовательности отсчетов, раскладывается на сомножители, затем вычисляются отдельные ДПФ меньших длин, чем N, из которых потом формируется выходная последовательность. Происходит так называемое расщепление исходного алгоритма на комбинацию подобных алгоритмов меньшего размера. БПФ содержит число мультипликативных операций (операций комплексного умножения) , число аддитивных операций (операций комплексного сложения) . [4]

Вычислительные преимущества БПФ по сравнению ДПФ следующие: БПФ содержит операций комплексного умножения в отличие от при ДПФ, таким образом, вычислительная экономия составляет / . Например, если N=1024, то экономия составляет 204,8 раза. БПФ содержит операций комплексного сложения в отличие от N(N-1) при ДПФ таким образом, вычислительная экономия составляет N(N-1) / . Например, если N=1024, то экономия составляет 102,3 раза