Вариант 1

Закон взаимодействия электрических зарядов экспериментально установлен в 1785 г. французским ученым Ш. Кулоном. Природа вещей такова, что сила взаимодействия между двумя небольшими заряженными шариками прямо пропорциональна произведению величин их зарядов и обратно пропорциональна квадрату расстояния между ними.

Сила взаимодействия зарядов - сила центральная, т. е. направлена вдоль прямой,соединяющей заряды (рис. 1.1). Для изотропной среды закон Кулона записывается следующим образом:

где k – коэффициент пропорциональности; q₁ и q₂ - величины взаимодействующих зарядов; r – расстояние между ними; r – радиус-вектор, проведенный от одного заряда к другому и направленный к тому из зарядов, на который действует сила.

Формулировка закона Кулона: «Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются».

Следует отметить, что закон Кулона применим для расчета взаимодействия точечных зарядов и тел шарообразной формы при равномерном распределении заряда по их поверхности или объёму.

Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел, несущих электрический заряд.

Экспериментальные исследования показали, что при прочих равных условиях сила электростатического взаимодействия зависит от свойств среды, в которой находятся заряды. Поэтому коэффициент пропорциональности k в законе Кулона представляют в виде k = k₁ / , где k₁  коэффициент, зависящий только от выбора системы единиц;   безразмерная величина, которая характеризует электрические свойства среды и называется относительной диэлектрическойпроницаемостью среды. Для вакуума  = 1.

В системе единиц СИ единица заряда кулон (Кл) определяется через единицу силы тока ампер (А) и единицу времени секунду (с), так что 1 Кл = 1 А1 с. Коэффициент k₁ в этой системе определяется следующим образом: k₁ = 1 / 4₀ = 8,98810⁹ (Нм²) / Кл², где ₀ = 8,8510^– Кл² / (Нм²) и носит названиеэлектрической постоянной.

Таким образом, закон Кулона для изотропной и однородной среды записывается в виде

 

2

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы   действующей на неподвижный^[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда  :

.

Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном^[2] множителе).

В каждой точке пространства в данный момент времени существует свое значение вектора   (вообще говоря - разное^[3] в разных точках пространства), таким образом,   - это векторное поле. Формально это выражается в записи

представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к.   может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле^[4], и законы, которым оно подчиняется, есть предмет электродинамики.

Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.

3

Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.

В СИ:  .

В СГС:  .

Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в СИ — в кулонах на м² (L⁻²TI). В рамках СТО векторы   и  объединяются в единый тензор, аналогичный тензору электромагнитного поля.

4

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

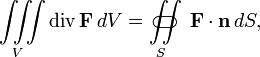
то есть интеграл от дивергенции векторного поля  , распространённый по некоторому объёму  , равен потоку вектора через поверхность  , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:

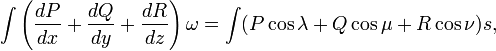
где   и   — дифференциалы объёма и поверхности соответственно. В современной записи   — элемент объёма,   — элемент поверхности.   — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

5

В предыдущей теме было показано, что взаимодействие между покоящимися зарядами осуществляется через электростатическое поле. Описание электростатического поля мы рассматривали с помощью вектора напряженности  , равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд

      Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать, что силы электростатического поля консервативны, а само поле потенциально.

      Рассмотрим поле, создаваемое неподвижным точечным зарядом  . В любой точке этого поля на пробный точечный заряд q действует сила 

,

где F(r)– модуль вектора силы  ,  – единичный вектор, определяющий положение заряда q относительно q´, ε₀ – электрическая постоянная.

      Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из раздела «Физические основы механики» известно, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек.

      Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2.

      Работа на пути dlравна:

      где dr – приращение радиус-вектора   при перемещении на dl;  т. е.

      Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу:

(3.1.1)

      Получили, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поляконсервативны, а само поле – потенциально.

      Этот вывод можно распространить и на поле, созданное системой зарядов, так как по принципу суперпозиции полей:  .

6

ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

Внутри диэлектрика может существовать электрическое поле!

Электрические свойства нейтральных атомов и молекул: Нейтральный атом -положительный заряд ( ядро) сосредоточен в центре; - отрицательный заряд - электронная оболочка;  считается, что из-за большой скорости движения электронов по орбитам центр распределения отрицательного заряда совпадает с центром атома. Молекула - чаще всего - это система ионов с зарядами противоположных знаков , т.к. внешние электроны слабо связаны с ядрами и могут переходить к другим атомам. Электрический диполь - молекула, в целом нейтральная , но центры распределения противоположных по знаку зарядов разнесены; рассматривается, как совокупность двух точечных зарядов, равных по модулю и противоположных по знаку, находящихся внутри молекулы на некотором расстоянии друг от друга. Существуют 2 вида диэлектриков ( различаются строением молекул) : 1) полярные - молекулы, у которых центры положительного и отрицательного зарядов не совпадают ( спирты, вода и др.);

2) неполярные - атомы и молекулы, у которых центры распределения зарядов совпадают (инертные газы, кислород, водород, полиэтилен и др.).

ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

Электростатическое поле - эл.поле, образованное неподвижными электрическими зарядами. Свободные электроны - электроны, способные свободно перемещаться внутри проводника ( в основном в металлах) под действием эл. поля; Свободные электроны возникают при образовании металлов: электроны с внешних оболочек атомов утрачивают связи с ядрами и начинают принадлежать всему проводнику;

- участвуют в тепловом движении и могут свободно перемещаться по всему проводнику. Электростатическое поле внутри проводника - внутри проводника электростатического поля нет ( Е = 0 ), что справедливо для заряженного проводника и для незаряженного проводника, внесенного во внешнее электростатическое поле.  Почему? - т.к. существует явление электростатической индукции, т.е.  явление разделения зарядов в проводнике, внесенном в электростатическое поле ( Евнешнее) с образованием нового электростатического поля ( Евнутр.) внутри проводника.

Внутри проводника оба поля ( Евнешн. и Евнутр.) компенсируют друг друга, тогда внутри проводника Е = 0. Заряды можно разделить:

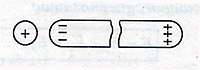
- металл. экран, внутри которого Е = 0, т.к. весь заряд будет сосредоточен на поверхности проводника. Электрический заряд проводников - весь статический заряд проводника расположен на его поверхности, внутри проводника q = 0; - справедливо для заряженных и незаряженных проводников в эл.поле. Линии напряженности эл.поля в любой точке поверхности проводника перпендикулярны этой поверхности.Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля.Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электростатической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее.Заземление — преднамеренное электрическое соединение какой-либо точки сети, электроустановки или оборудования с заземляющим устройством.

Вариант 2

Мембранный потенциал (реже - трансмембранный потенциал) - разность электрических потенциалов между растворами электролитов, разделенных проницаемой мембраной.

Роль мембраны в первую очередь состоит в создании препятствия к смешиванию растворов, расположенных по её разные стороны. Мембрана может быть либо электрически индифферентной, диффузия через которую возможна для всех частиц, имеющихся в растворе; либо полупроницаемой (активной), через такую мембрану некоторые частицы пройти не могут (см. осмос).

Мембранный потенциал имеет огромное значение в жизни многоклеточных существ. Он связан с работой натриевой протонной помпы, других механизмов саморегуляции клеточного обмена; с устойчивостью таких клеток, как эритроциты, но особенно хорошо видна роль мембранного потенциала при анализе работы нервных клеток. Клетки животных ограничены липопротеидноймембраной, являющейся электрическим изолятором. Между содержимым клетки и внеклеточной жидкостью формируется и поддерживается определённое значение разности потенциалов, так называемый мембранный потенциал.

Пассивный транспорт. Если вещество движется через мембрану из области с высокой концентрацией в сторону низкой концентрации (т. е. по градиенту концентрации этого вещества) без затраты клеткой энергии, то такой транспорт называется пассивным, или диффузией. Различают два типа диффузии: простую и облегченную.

Активный транспорт. Имеет место в том случае, когда перенос осуществляется против градиента концентрации. Такой перенос требует затраты энергии клеткой. Активный транспорт служит для накопления веществ внутри клетки. Источником энергии часто является АТФ. Для активного транспорта кроме источника энергии необходимо участие мембранных белков. Одна из активных транспортных систем в клетке животных отвечает за перенос ионов Na+ и K+ через клеточную мембрану. Эта система называется Na+ - K+ - насос. Она отвечает за поддержание состава внутриклеточной среды, в которой концентрация К+ выше, чем Na+.

Уравнение Нернста — уравнение, связывающее окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, истандартными электродными потенциалами окислительно-восстановительных пар.

,

где

•  — электродный потенциал, 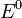  — стандартный электродный потенциал, измеряется в вольтах;

•  — универсальная газовая постоянная, равная 8.31 Дж/(моль·K);

•  — абсолютная температура;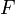

•  — постоянная Фарадея, равная 96485,35 Кл·моль⁻¹;

•  — число моль электронов, участвующих в процессе;

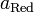•  и   — активности соответственно окисленной и восстановленной форм вещества, участвующего в полуреакции.

Если в формулу Нернста подставить числовые значения констант   и   и перейти от натуральных логарифмов к десятичным, то при   получим

Уравнение Гольдмана в приближении постоянного поля

= const

описывает пассивный поток через мембрану:

,где

F - число Фарадея,  Z - валентность иона,  T - абсолютная температура,  R - газовая постоянная,   - электрический потенциал на мембране,  P - коэффициент проницаемости,  C_o - концентрация наружного омывающего мембрану раствора электролита,  C_i - концентрация внутреннего раствора.

Уравнение Гольдмана предсказывает нелинейную зависимость трансмембранного потока ионов от разности потенциалов на мембране.

Силой тока называется физическая величина  , равная отношению количества заряда  , прошедшего за некоторое время   через поперечное сечение проводника, к величине этого промежутка времени.

Вариант 4

Сила тока в системе СИ измеряется в Амперах.

По закону Ома сила тока   для участка цепи прямо пропорциональна приложенному напряжению   к участку цепи и обратно пропорциональна сопротивлению   проводника этого участка цепи :

 — где e — заряд электрона, n — концентрация частиц, S — площадь поперечного сечения проводника,   — средняя скорость упорядоченного движения электронов.

Единица измерения в СИ — 1 Ампер (А) = 1 Кулон / секунду.

Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).

В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).

Напряжение:

• Электрическое напряжение между точками A и B — отношение работы электрического поля при переносе пробного заряда из точки A в B к величине этого пробного заряда.

  • Номинальное напряжение

  • Сетевое напряжение

  • Шаговое напряжение

• Механическое напряжение — мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий.

  • Тензор напряжений — наиболее общее математическое выражение механического напряжения.

  • Напряжение сдвига

  • Касательное напряжение

  • Нормальное напряжение

  • Температурное напряжение

• Психологическое напряжение — состояние в ожидании возникновения негативных эмоций, например, страха

• Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождениюэлектрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему^[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением(резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

• Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

• 

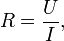
• где

• R — сопротивление;

• U — разность электрических потенциалов на концах проводника;

• I — сила тока, протекающего между концами проводника под действием разности потенциалов.

• Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источникахпостоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительногозаряда вдоль контура.

• ЭДС можно выразить через напряжённость электрического поля сторонних сил ( 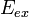). В замкнутом контуре ( ) тогда ЭДС будет равна: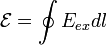

• , где 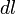  — элемент длины контура.

• ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

Закон Джоуля — Ленца-Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

где   — мощность выделения тепла в единице объёма,   — плотность электрического тока,   — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивлению участка

В математической форме этот закон имеет вид

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ доt₂. В случае постоянных силы тока и сопротивления:

Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.

Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (на­пряжению) и силе тока в цепи.

Для измерения мощности электрического тока принята еди­ница, называемая ватт (Вт).

Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В.

Для вычисления мощности постоянного тока в ваттах нуж­но силу тока в амперах умножить на напряжение в вольтах.

Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы

P = I*U. 

Определения Правила Кирхгофа

Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U₁, I₁ есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Терминзамкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

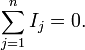
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений 

для переменных напряжений 

Вариант 5

Электровакуумный диод — вакуумная двухэлектродная электронная лампа. Катод диода нагревается до температур, при которых возникает термоэлектронная эмиссия. При подаче на анод отрицательного относительно катода напряжения все эмитированные катодом электроны возвращаются на катод, при подаче на анод положительного напряжения часть эмитированных электронов устремляется к аноду, формируя его ток. Таким образом, диод выпрямляет приложенное к нему напряжение. Это свойство диода используется для выпрямления переменного тока и детектирования сигналов высокой частоты. Практический частотный диапазон традиционного вакуумного диода ограничен частотами до 500 МГц. Дисковые диоды, интегрированные в волноводы, способны детектировать частоты до 10 ГГц^[1].

Устройство

Обозначение на схемах диода с катодом непрямого накала.

Электровакуумный диод представляет собой сосуд (баллон), в котором создан высокий вакуум. В баллоне размещены два электрода — катод и анод. Катод прямого накала представляет собой прямую или W-образную нить, разогреваемую током накала. Катод косвенного накала — длинный цилиндр или короб, внутри которых уложена электрически изолированная спираль подогревателя. Как правило, катод вложен внутрь цилиндрического или коробчатого анода, который в силовых диодах может иметь рёбра или «крылышки» для отвода тепла. Выводы катода, анода и подогревателя (в лампах косвенного накала) соединены с внешними выводами (ножками лампы).